Benützer:
Anwendung in Mikroskopen
Storyboard 
Das Prinzip des Mikroskops besteht darin, das kleine Bild zu erfassen, das oben als parallele Strahlen vorliegt, und es mit einer bikonvexen Linse zu vergrößern, um ein größeres invertiertes reales Bild zu erzeugen.
ID:(299, 0)
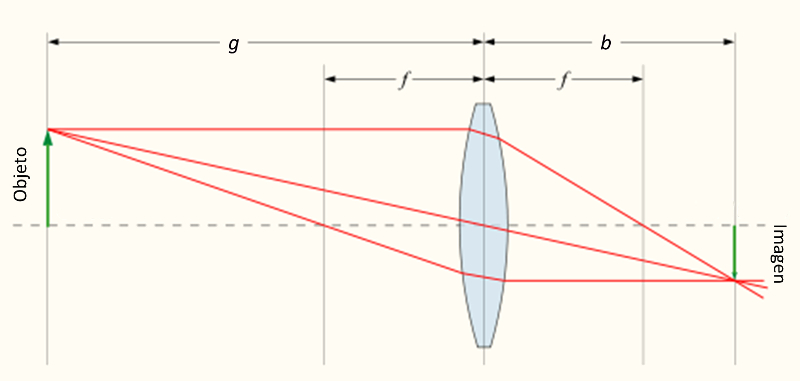
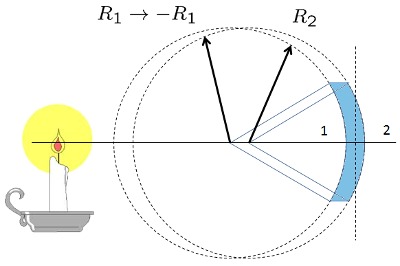
Strahlgeometrie in einer Linse in der Nähe eines Objekts
Bild
Für den Fall, dass sich das Objekt näher am Objektiv als am Brennpunkt befindet, ist das Diagramm zur Bestimmung von Bildgröße und Position etwas komplexer. In diesem Fall müssen die Balken sein
- projiziert von wo sie das Objekt erreicht hätten, das sie ausstrahlt
- Innerhalb der Projektion müssen die gleichen Regeln wie bei einem realen Strahl eingehalten werden
In diesem Fall reicht es aus, die gleichen drei Strahlen erneut zu zeichnen:
- Parallel zur optischen Achse wird durch den Fokus gebrochen
- über den Fokus wird parallel zur optischen Achse gebrochen
- über den Ursprung der durchgehenden optischen Achse in einer geraden Linie
und das Bild wird auf die gleiche Weise erhalten:
ID:(9783, 0)
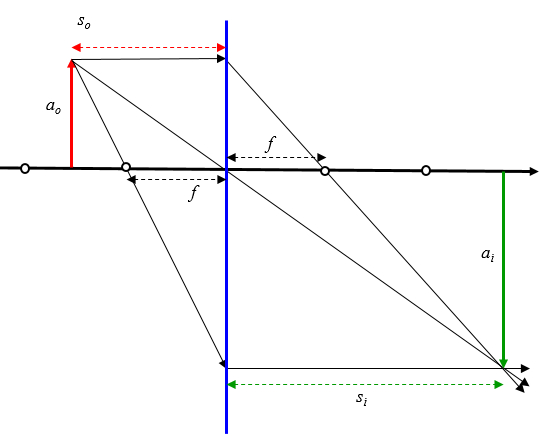
Geometrie der Strahlen auf einem Objektiv
Bild
Bei einer Bikonvexlinse ein Strahl, der auf die Linse trifft
- Parallel zur optischen Achse wird durch den Fokus gebrochen
- über den Fokus wird parallel zur optischen Achse gebrochen
- über den Ursprung der durchgehenden optischen Achse in einer geraden Linie
Was im Fall eines Objekts in einer Entfernung größer als das Foto entspricht:
ID:(1856, 0)
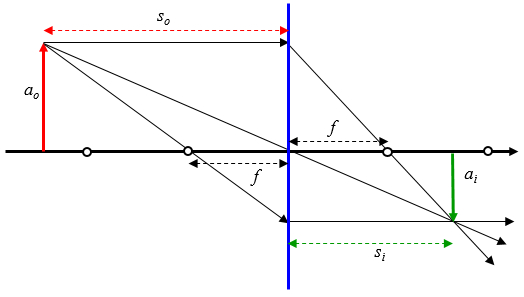
Konvexe Linse
Bild
Eine konvexe Linse ist eine Linse, die den parallelen Lichtstrahl, der parallel durch ihren Fokus fällt, bricht:
ID:(1855, 0)
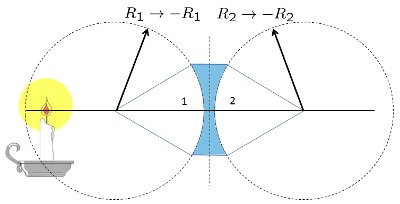
Position und Fokus von einer Konvexen Linse
Gleichung
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
 $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relación de similitud de los triángulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
ID:(3347, 0)
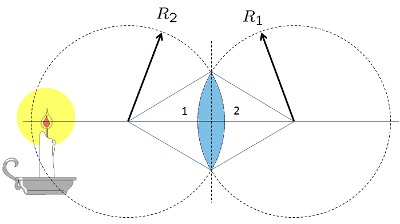
Proportionen der Größe und Position von einer konkaven Linse
Gleichung
Für jedes Objektiv können Sie charakteristische Strahlen zeichnen, mit denen Sie auf ähnliche Weise zeigen können, dass die Größen des Objekts und des Bildes im gleichen Verhältnis stehen wie ihre Abstände zum optischen Element (Objektiv oder Spiegel).
Wenn das Objekt eine Größe
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
ID:(3346, 0)
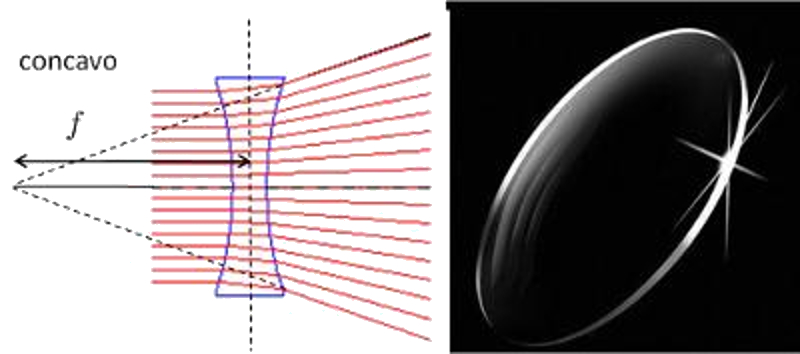
Konkave Linse
Bild
Konvexlinsen sind in ihrer Mitte dünner und weiten sich zu den Rändern hin aus.
Die parallel auftreffenden Lichtstrahlen werden gestreut, als ob das Licht im Linsenfokus abgestrahlt würde.
ID:(1854, 0)
Berechnung des Fokus einer Einfache Bikonvexlinse
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
ID:(3432, 0)
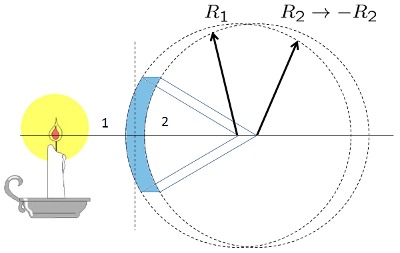
Berechnung des Fokus eines bikonvexe dicken Linse
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracción
| $\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
ID:(3348, 0)
Cálculo del foco de un lente convexo-concavo grueso simétrico
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
ID:(3430, 0)
Cálculo del foco de un lente convexo-cóncavo grueso
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
| $\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$ |
ID:(3350, 0)
Berechnung des Fokus einer einfachen Bikonkaven Linse
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
ID:(3431, 0)
Cálculo del foco de un lente concavo-convexo grueso simétrico
Gleichung
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
ID:(3429, 0)
Die Berechnung des Fokus einer bi-konkave dicken Linse
Gleichung
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
| $\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
ID:(3349, 0)
Multiples lentes
Bild
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:
ID:(9465, 0)
Brechung abhängig von der Lichtfarbe
Bild
Der Brechungsindex von Glas kann von der Wellenlänge oder Frequenz des Lichts abhängen. In diesem Fall spricht man von einem 'chromatischen' Glas. Wenn es diese Eigenschaft nicht aufweist, wird es als 'achromatisch' bezeichnet.
Das Hauptproblem dieser Eigenschaft besteht darin, dass die Position des Fokus einer Linse von der Farbe des Lichts abhängt. Daher hat eine optische Linse das Problem, dass das Auge einen Farbfokus einstellen kann, aber nicht gleichzeitig für Objekte in anderen Farben.
ID:(1626, 0)