Foco de Lente
Storyboard 
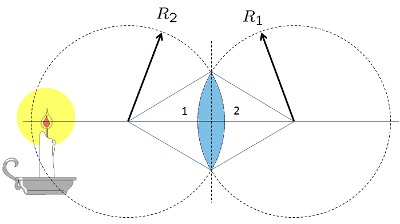
El foco de un lente se puede calcular de los radios de curvatura de ambos lados del lente.
En el caso de un lente de grosor finito el foco depende ademas del indice de refracción del medio (vidrio) y del grosor en el eje óptico.
ID:(1442, 0)
Formula simplificada del fabricante de lentes
Ecuación 
En su versión simplificada (que no depende del grosor del lente) el foco de un lente
ID:(10924, 0)
Cálculo del foco de un lente bi-convexo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracción
ID:(3348, 0)
Cálculo del fóco de un lente bi-convexo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3432, 0)
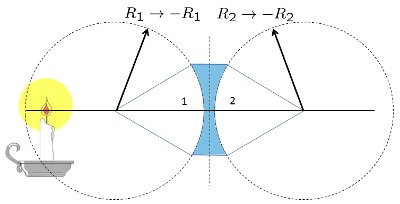
Cálculo del foco de un lente bi-cóncavo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
ID:(3349, 0)
Cálculo del fóco de un lente bi-concavo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3431, 0)
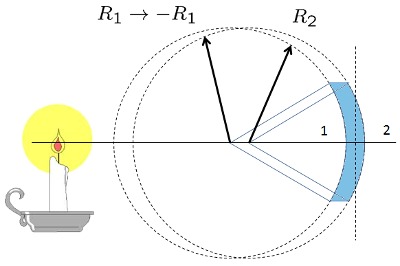
Cálculo del foco de un lente cóncavo-convexo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción n, un grosor en el centro de d y las curvaturas son R_1 y R_2, se puede calcular el foco f. Para ello basta tomar la ecuación del lente bi-convexo e introducir el radio de curvatura R_1 con el signo negativo:
Lente bi-convexo de grosor no despreciable
ID:(3351, 0)
Cálculo del foco de un lente concavo-convexo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3429, 0)
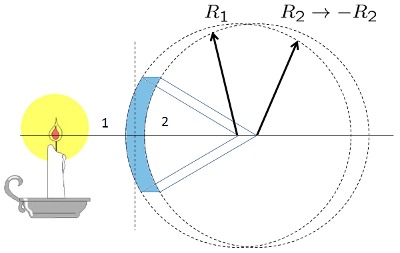
Cálculo del foco de un lente convexo-cóncavo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
ID:(3350, 0)
Cálculo del foco de un lente convexo-concavo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3430, 0)
0
Video
Video: Foco de Lente