User:
Concave Lenses
Storyboard 
The concave lenses diverge the incident beam by emitting the beams as if they were coming from a focal point on the side on which the beam strikes.
ID:(1267, 0)
Concave Lens
Image
Convex lenses are thinner in their center widening towards the edges.
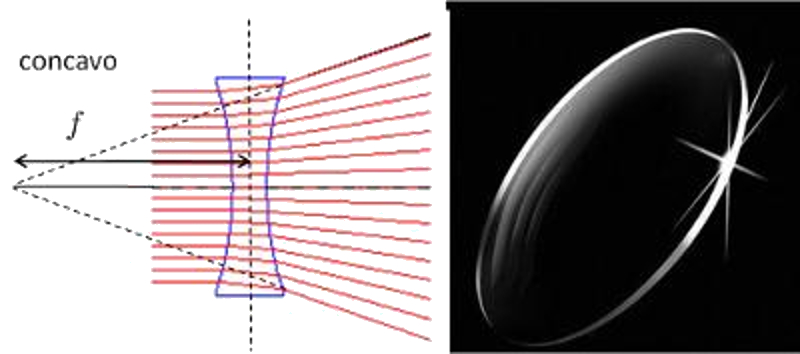
The light beams that have a parallel impact are scattered as if the light were emitted in the lens focus.
ID:(1854, 0)
Calculo de imagen para un lente concavo
Image
Para poder calcular el tamaño y el lugar en que se presentara la imagen se puede dibujar el eje óptico, el lente concavo y un objeto en una posición y de un tamaño. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje óptico que tras incidir sobre el lente continua a lo largo de una linea que sale del foco del mismo lado que el objeto
• Un haz que pasa por el centro del lento continua en una linea recta al otro lado del lente.
• Un haz que pasaría por el foco al otro lado del lente pero que dibuja paralelo al eje óptico
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posición, el tamaño de la imagen y si esta invertida o no.
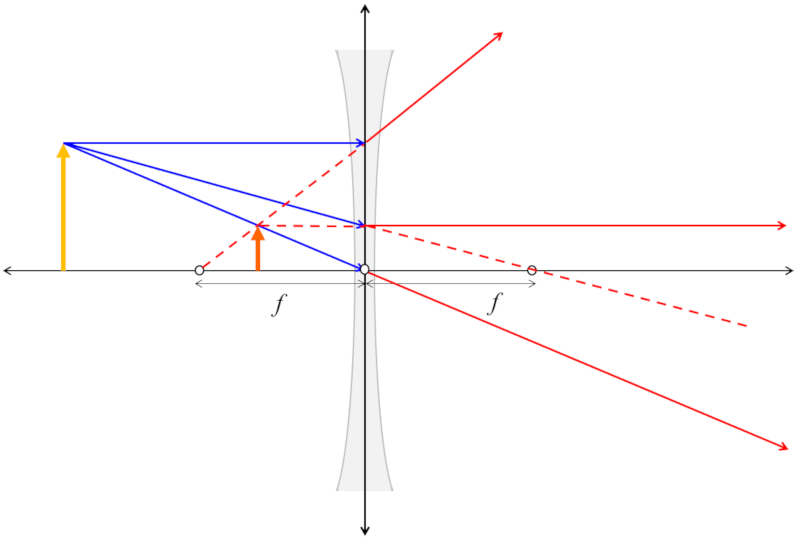
ID:(12693, 0)
Similitud tamaños y posiciones
Image
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
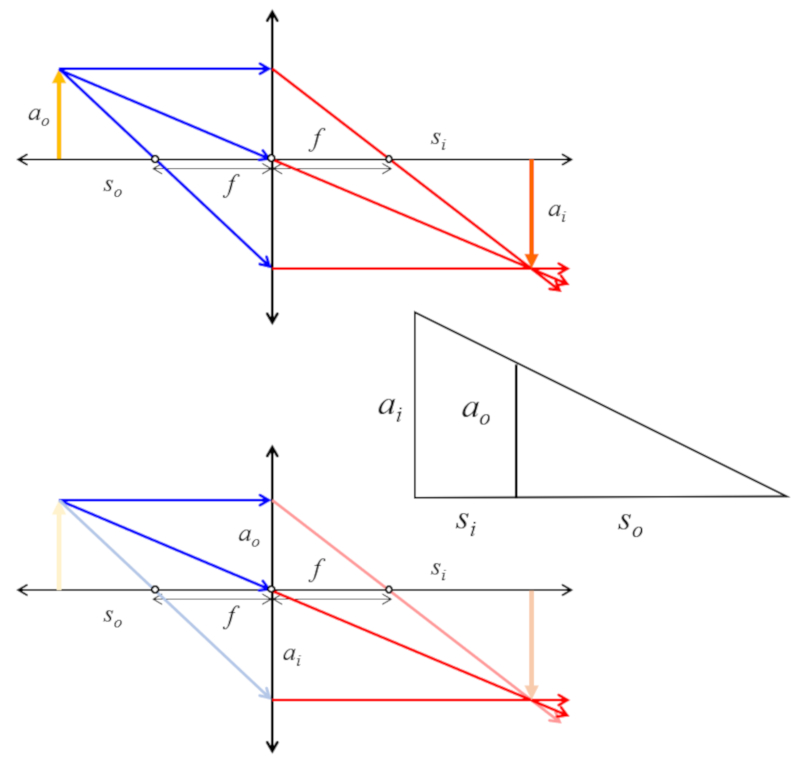
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Image
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
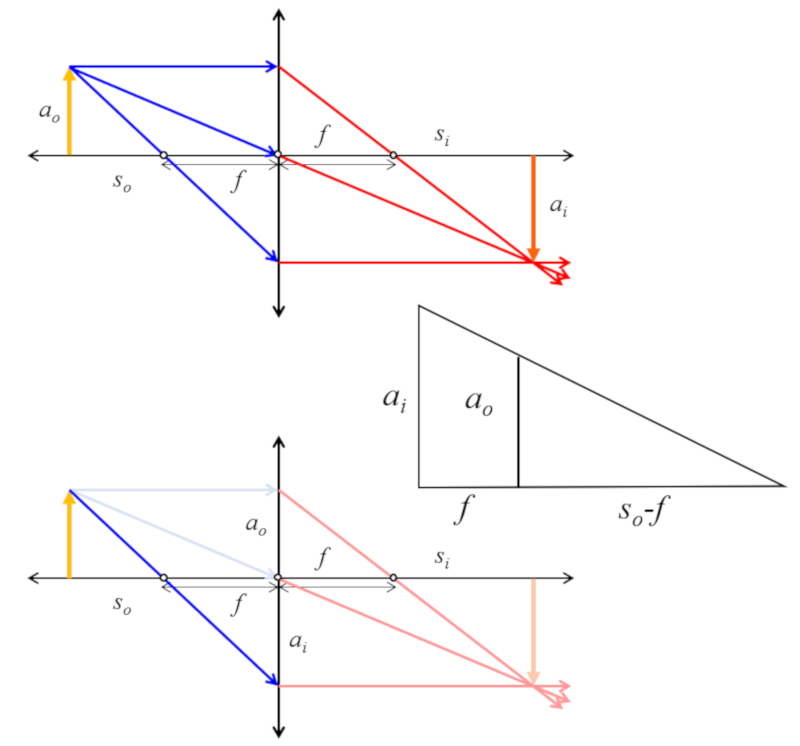
ID:(12698, 0)
Lente concavo con objeto entre origen y foco
Image
Si se asume que el objeto esta entre el origen del eje óptico y el foco se tiene:
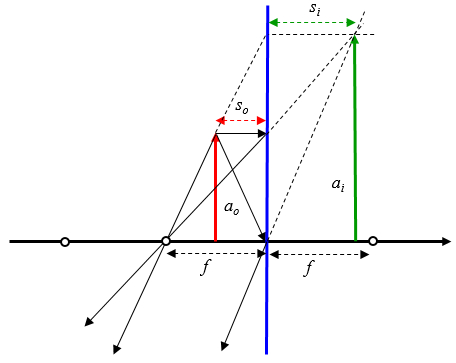
ID:(12690, 0)
Lente concavo con objeto entre el foco y el doble del foco
Image
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
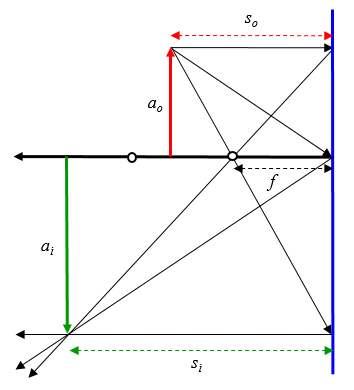
ID:(12691, 0)
Lente concavo con objeto mas lejos que el doble del foco
Image
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
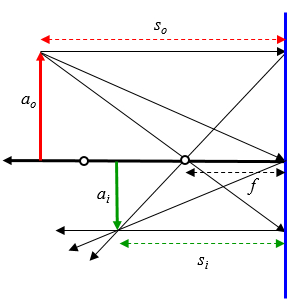
ID:(12692, 0)
Simulación de un lente cóncavo
Description
La forma como opera el lente se puede simular con
ID:(14046, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$
a_o / a_lc = s_o / s_lc
$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$
1/ f_lc =1/ s_o +1/ s_lc
ID:(16062, 0)
Proportions size and position of concave lens
Equation
For any lens you can draw characteristic beams with which you can similarly show that the sizes of the object and the image are in the same proportion as their distances to the optical element (lens or mirror).
If the object has a size
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
ID:(3346, 0)
Position and focus of concave lens
Equation
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relación de similitud de los triángulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
ID:(3347, 0)