Utilisateur:
Moment d'inertie de la barre, axe perpendiculaire
Storyboard 
Le moment d'inertie est l'équivalent en rotation de la masse dans un mouvement de translation. Dans le cas d'une barre tournant autour d'un axe perpendiculaire à son propre axe, le cas le plus simple se présente lorsque la rotation s'effectue autour du centre de masse.
ID:(2090, 0)
Moment d'inertie pour un axe qui ne passe pas par le centre de masse
Description
Lorsque l'axe de rotation ne passe pas par le centre de masse (CM), le moment d'inertie $I$ peut être calculé à l'aide du Théorème de Steiner. Pour ce faire, on commence par le moment d'inertie par rapport au centre de masse, par exemple :
• Pour une barre avec un axe perpendiculaire, il est calculé
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
• Pour un cylindre avec un axe perpendiculaire, il est calculé
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
• Pour un cylindre avec un axe parallèle, il est calculé
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
• Pour un parallélépipède, il est calculé
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
• Pour un cube, il est calculé
| $ I_{CM} =\displaystyle\frac{1}{6} m a ^2$ |
• Pour une sphère, il est calculé
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
Ensuite, la masse multipliée par le carré de la distance entre l'axe de rotation et le centre de masse est ajoutée
| $ I = I_{CM} + m d ^2$ |
ID:(15867, 0)
Barre qui tourne autour d'un axe $\perp$
Image
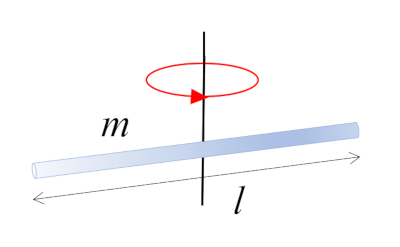
Une barre de masse $m$ et de longueur $l$ qui tourne autour de son centre, qui coïncide avec le centre de masse :
ID:(10962, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ I = I_{CM} + m d ^2$
I = I_CM + m * d ^ 2
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ \omega = \omega_0 + \alpha_0 ( t - t_0 )$
omega = omega_0 + alpha_0 * ( t - t_0 )
$ T = I \alpha_0 $
T = I * alpha
$ T = r F $
T = r * F
$ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$
theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2
$ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$
theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )
ID:(15859, 0)
Moment d'inertie de la barre de longueur $l$ axe $\perp$
Équation
Le moment d'inertie d'une barre en rotation autour d'un axe perpendiculaire ($\perp$) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
.
ID:(4432, 0)
Théorème de Steiner
Équation
A moment d\'inertie de l\'axe qui ne passe pas par le CM ($I$) peut être calculé en utilisant a moment d\'inertie du centre de masse ($I_{CM}$) et en ajoutant le moment d'inertie de a masse corporelle ($m$) comme s'il s'agissait d'une masse ponctuelle à A distance centre de masse et axe ($d$) :
| $ I = I_{CM} + m d ^2$ |
ID:(3688, 0)
Couple pour moment d'inertie constant
Équation
Dans le cas où le moment d'inertie est constant, la dérivée du moment angulaire est égale à
| $ L = I \omega $ |
ce qui implique que le couple est égal à
| $ T = I \alpha_0 $ |
| $ T = I \alpha $ |
Comme le moment est égal à
| $ L = I \omega $ |
il en découle que dans le cas où le moment d'inertie ne change pas avec le temps,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
ce qui implique que
| $ T = I \alpha $ |
.
Cette relation correspond à l'équivalent de la deuxième loi de Newton pour la rotation au lieu de la translation.
ID:(3253, 0)
Relation simple couple - force
Équation
Puisque la relation entre le moment angulaire et le moment est
| $ L = r p $ |
sa dérivée temporelle nous conduit à la relation du moment de force
| $ T = r F $ |
La rotation du corps se produit autour d'un axe dans la direction du moment de force, qui passe par le centre de masse.
ID:(4431, 0)
Vitesse angulaire avec accélération angulaire
Équation
Avec a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) établit une relation linéaire avec le temps ($t$), intégrant également les variables a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$) comme suit :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Si nous supposons que a accélération angulaire moyenne ($\bar{\alpha}$) est constant, équivalent à A accélération angulaire constante ($\alpha_0$), alors l'équation suivante s'applique :
| $ \bar{\alpha} = \alpha_0 $ |
Par conséquent, en considérant a différence de vitesses angulaires ($\Delta\omega$) avec a vitesse angulaire ($\omega$) et a vitesse angulaire initiale ($\omega_0$) :
| $ \Delta\omega = \omega - \omega_0 $ |
et le temps écoulé ($\Delta t$) en relation avec le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
l'équation pour a accélération angulaire moyenne ($\bar{\alpha}$) :
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
peut être exprimée comme suit :
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
En résolvant cela, nous obtenons :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Cette équation représente une droite dans le plan de la vitesse angulaire par rapport au temps.
ID:(3237, 0)
Angle pour accélération angulaire constante
Équation
Étant donné que le déplacement total correspond à l'aire sous la courbe de vitesse angulaire par rapport au temps, dans le cas de une accélération angulaire constante ($\alpha_0$), il est déterminé que le déplacement le angle ($\theta$) avec les variables le angle de départ ($\theta_0$), le temps ($t$), le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) est le suivant :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Dans le cas de a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) en fonction de le temps ($t$) suit une relation linéaire avec le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) sous la forme :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Étant donné que le déplacement angulaire est égal à l'aire sous la courbe de vitesse angulaire-temps, dans ce cas, on peut ajouter les contributions du rectangle :
$\omega_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Cela nous mène à l'expression pour le angle ($\theta$) et le angle de départ ($\theta_0$) :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Cette expression correspond à la forme générale d\'une parabole.
ID:(3682, 0)
Angle de freinage en fonction de la vitesse angulaire
Équation
Dans le cas de a accélération angulaire constante ($\alpha_0$), la fonction de a vitesse angulaire ($\omega$) par rapport à Le temps ($t$), avec les variables supplémentaires a vitesse angulaire initiale ($\omega_0$) et le temps initial ($t_0$), est exprimée par l'équation :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
À partir de cette équation, il est possible de calculer la relation entre le angle ($\theta$) et le angle de départ ($\theta_0$), ainsi que le changement de vitesse angulaire :
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
Si nous résolvons le temps dans l'équation de a vitesse angulaire ($\omega$) qui inclut les variables a vitesse angulaire initiale ($\omega_0$), le temps ($t$), le temps initial ($t_0$) et a accélération angulaire constante ($\alpha_0$) :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
nous obtenons l'expression suivante pour le temps :
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Cette solution peut être substituée dans l'équation pour calculer le angle ($\theta$) en utilisant le angle de départ ($\theta_0$) de la manière suivante :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
ce qui donne la formule suivante :
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
ID:(4386, 0)