Théorème de Steiner
Équation 
A moment d\'inertie de l\'axe qui ne passe pas par le CM (I) peut être calculé en utilisant a moment d\'inertie du centre de masse (I_{CM}) et en ajoutant le moment d'inertie de a masse corporelle (m) comme s'il s'agissait d'une masse ponctuelle à A distance centre de masse et axe (d) :
ID:(3688, 0)
Application du théorème de Steiner pour un cylindre, axe \parallel
Image 
Pour un cylindre avec un axe parallèle à son propre axe :
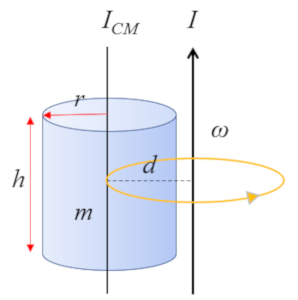
dont le moment d'inertie par rapport au centre de masse (CM) est donné par
| I_{CM} =\displaystyle\frac{1}{2} m r_c ^2 |
le moment d'inertie peut être calculé en utilisant le théorème de Steiner avec la formule suivante
| I = I_{CM} + m d ^2 |
.
ID:(11551, 0)
Application du théorème de Steiner pour un cylindre d'axe \perp
Image 
Pour un cylindre avec un axe perpendiculaire à son propre axe :
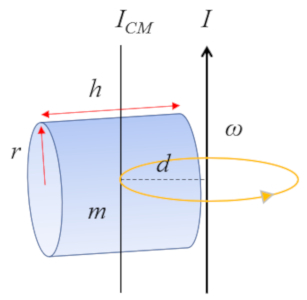
dont le moment d'inertie par rapport au centre de masse (CM) est défini comme
| I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2) |
le calcul du moment d'inertie peut être effectué en utilisant le théorème de Steiner avec la formule suivante
| I = I_{CM} + m d ^2 |
.
ID:(11552, 0)
Application du théorème de Steiner pour un parallélépipède droit
Image 
Pour un parallélépipède rectangle d'axe parallèle à une arête:
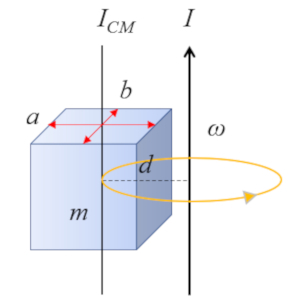
dont le moment d'inertie par rapport au centre de masse (CM) est défini comme
| I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2) |
le calcul du moment d'inertie peut être effectué en utilisant le théorème de Steiner avec la formule suivante
| I = I_{CM} + m d ^2 |
.
ID:(11554, 0)
Application du théorème de Steiner pour une sphère
Image 
Pour une sphère avec un axe à une distance de son centre :

dont le moment d'inertie par rapport au centre de masse (CM) est défini comme
| I_{CM} =\displaystyle\frac{2}{5} m r_e ^2 |
le calcul du moment d'inertie peut être effectué en utilisant le théorème de Steiner avec la formule suivante distance centre de masse et axe m, masse corporelle kg, moment d\'inertie de l\'axe qui ne passe pas par le CM kg m^2 et moment d\'inertie du centre de masse kg m^2
| I = I_{CM} + m d ^2 |
.
ID:(11553, 0)
0
Video
Vidéo: Théorème de Steiner
