User:
Stokes force
Storyboard 
An example of viscous force is the model that arises when a sphere moves within a viscous medium. This model and the associated equation are known by the name of their author, George Stokes.
The Stokes' force depends on the viscosity of the medium, the radius of the sphere, and the velocity at which it moves through the medium. Similarly, if the medium itself is in motion, it drags the object along with it.
ID:(1964, 0)
Mechanisms
Iframe
Mechanisms
ID:(15540, 0)
George Stokes
Description
George Stokes made significant contributions to the fields of hydrodynamics and mathematics. He is primarily remembered for the well-known Stokes\' law applied to spherical bodies in a fluid flow and for the Stokes\' theorem in mathematics.
George Gabriel Stokes (1819-1903)
ID:(12535, 0)
Forces on a sphere falling in a medium
Description
When a sphere is thrown into a viscous medium, there's an initial upward force, a gravitational Force ($F_g$), which gradually sinks the body. During this process, the sphere gains velocity, resulting in a downward force, a viscose force ($F_v$), which depends on the velocity. As the total velocity, the force with constant mass ($F$),
| $ F = F_g - F_v $ |
begins to decrease until it becomes null. From this moment on, the movement continues at a constant velocity since there's no force to accelerate it.
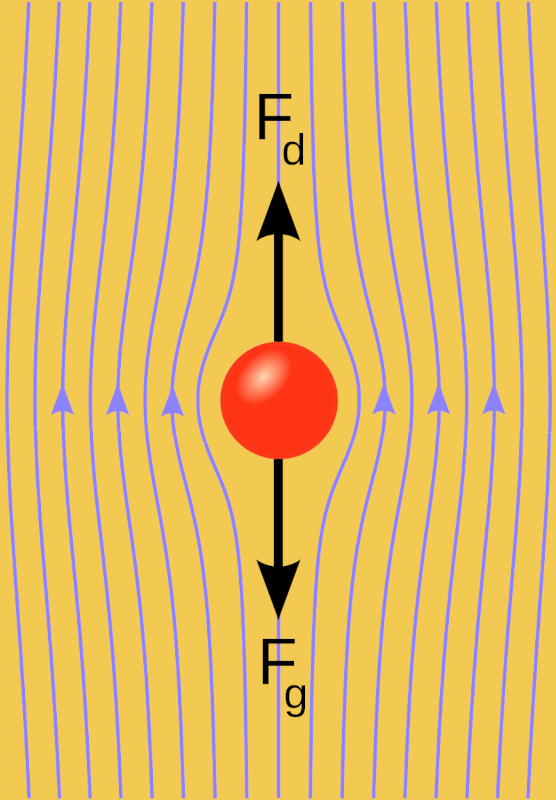
ID:(15544, 0)
Stokes force
Top
The Stokes force is the force generated by the flow around a sphere of the radio de la Gota ($r$) immersed in it. In this case, the model of force proportional to the speed ($v$) is used:
| $ F_v = b v $ |
In this context, it can be shown that the constant of the Viscose Force ($b$) with the viscosity ($\eta$) is equal to:
| $ b \equiv 6 \pi \eta r $ |
therefore, the Stokes force is expressed as:
| $ F_v =6 \pi \eta r v $ |
This force is mainly applied in laminar flows.
ID:(15555, 0)
Fall speed in viscous medium
Top
The motion of a sphere in two dimensions is characterized by the component x of velocity ($v_x$) with the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
and the component y of velocity ($v_y$) with the initial vertical speed ($v_{0y}$), the adaptation time ($\tau$), the gravitational Acceleration ($g$), and the time ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
which is represented in an $v_x$ vs $v_y$ diagram:
The diagram shows how both velocity components evolve over time. Initially, $v$ equals $v_{0x}$, which corresponds to a point on the right edge of the graph. Over time, the velocity components evolve from the right side to the left edge, where the horizontal velocity is zero and the vertical velocity reaches the limit $g\tau$, so $v/g\tau$ equals one.
ID:(15558, 0)
Fall path in viscous medium
Top
The horizontal displacement can be calculated using the equation for the position on the x-axis ($x$) with the initial position on the x-axis ($x_0$), the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
and the vertical displacement for the position on the y-axis ($y$) with the initial position on the y-axis ($y_0$), the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
which is graphed in the positions $x$ vs $y$:
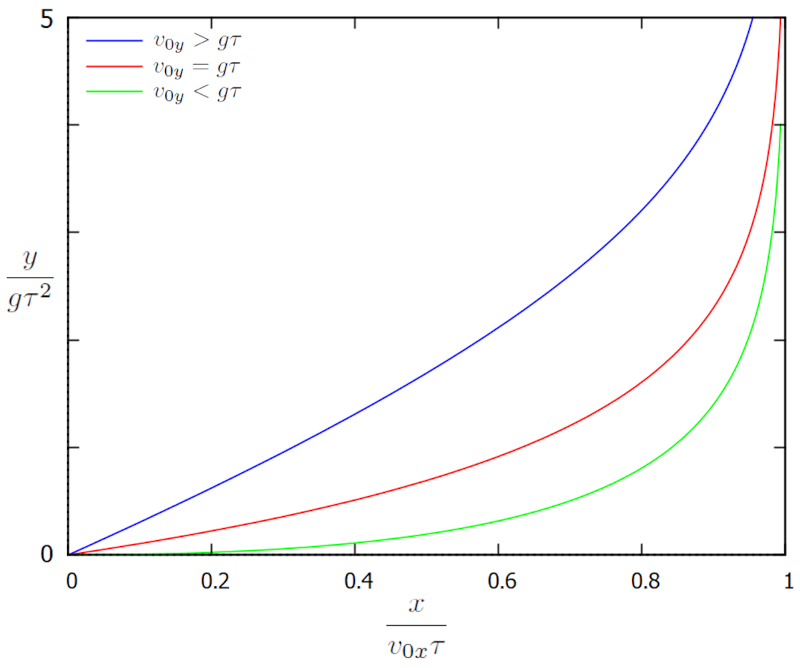
In this case, the position evolves from the left edge to the right, where it stops in its horizontal movement, reaching a maximum distance of $v_{0x}\tau$. The vertical displacement is described with a coordinate system whose origin is at the point where the trajectory begins and whose vertical version points downwards. In this sense, the increase in $y$ corresponds to the descent of the sphere in the direction of gravity.
ID:(15559, 0)
Ostwald method for measuring viscosity
Description
The Ostwald viscosity measurement method is based on the behavior of a liquid flowing through a small-radius tube (capillary).
The liquid is introduced, suction is applied to exceed the upper mark, and then it is allowed to drain, measuring the time it takes for the level to pass from the upper to the lower mark.
The experiment is conducted first with a liquid for which viscosity and density are known (e.g., distilled water), and then with the liquid for which viscosity is to be determined. If conditions are identical, the liquid flowing in both cases will be similar, and thus, the time will be proportional to the density divided by the viscosity. Thus, a comparison equation between both viscosities can be established:
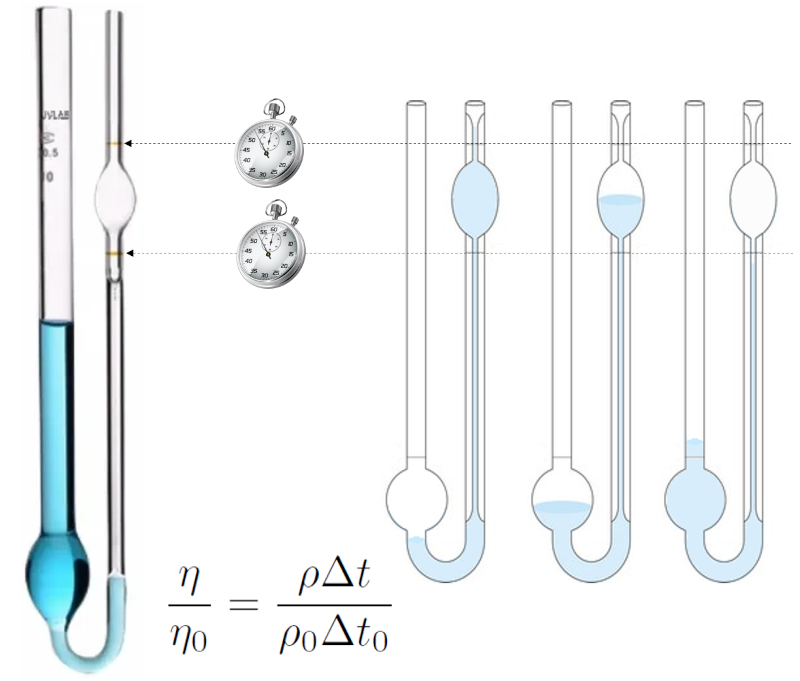
ID:(15545, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ b \equiv 6 \pi \eta r $
b = 6* pi * eta * r
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ F_v =6 \pi \eta r v $
F_v =6* pi * eta * r * v
$ m_g = m_i $
m_g = m_i
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ \rho \equiv\displaystyle\frac{ m_i }{ V }$
rho = M / V
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ V =\displaystyle\frac{4 \pi }{3} r ^3$
V =4* pi * r ^3/3
$ v_x = v_{0x} e^{- t / \tau }$
v_x = v_0x *exp(- t / tau )
$ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$
v_y = g * tau + ( v_0y - g * tau )*e^(- t / tau )
$ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$
x = x_0 + v_0x * tau *(1-e^(- t / tau ))
$ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$
y = y_0 + tau * g * t + tau *( v_0y - g * tau )*(1-e^(- t / tau ))
$\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$
tau = 2* r ^2* rho /(9 * eta )
ID:(15542, 0)
Total force of body falling in viscous medium
Equation
In the case of a body falling in a viscous medium, the total force, the force with constant mass ($F$), is equal to the gravitational Force ($F_g$) minus the viscose force ($F_v$), so
| $ F = F_g - F_v $ |
ID:(15543, 0)
Force case constant mass
Equation
In the case where the inertial Mass ($m_i$) equals the initial mass ($m_0$),
| $ m_g = m_i $ |
the derivative of momentum will be equal to the mass multiplied by the derivative of the speed ($v$). Since the derivative of velocity is the instant acceleration ($a$), we have that the force with constant mass ($F$) is
| $ F = m_i a $ |
Since the moment ($p$) is defined with the inertial Mass ($m_i$) and the speed ($v$),
| $ p = m_i v $ |
If the inertial Mass ($m_i$) is equal to the initial mass ($m_0$), then we can derive the momentum with respect to time and obtain the force with constant mass ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Therefore, we conclude that
| $ F = m_i a $ |
ID:(10975, 0)
Gravitational Force
Equation
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_g = m_g g $ |
ID:(3241, 0)
Viscose Force
Equation
The simplest form of the viscose force ($F_v$) is one that is proportional to the the speed ($v$) of the body, represented by:
| $ F_v = b v $ |
The proportionality constant, also known as the constant of the Viscose Force ($b$), generally depends on the shape of the object and the viscosity of the medium through which it moves. An example of this type of force is the one exerted by a fluid stream on a spherical body, whose mathematical expression is known as Stokes' law.
ID:(3243, 0)
Stokes force
Equation
The resistance is defined in terms of the fluid viscosity and the sphere's velocity as follows:
| $ F_v = b v $ |
Stokes explicitly calculated the resistance experienced by the sphere and determined that viscosity is proportional to the sphere's radius and its velocity, leading to the following equation for resistance:
| $ F_v =6 \pi \eta r v $ |
ID:(4871, 0)
Stokes force factor
Equation
In the case of the Stokes force in the viscose force ($F_v$), it is modeled with the constant of the Viscose Force ($b$) and the speed ($v$),
| $ F_v = b v $ |
which corresponds to a value of the constant of the Viscose Force ($b$) that, with the viscosity ($\eta$) and the radio de la Gota ($r$), is equal to
| $ b \equiv 6 \pi \eta r $ |
ID:(15554, 0)
Equation of motion falling in a viscous medium
Equation
The force with constant mass ($F$) equals the gravitational Force ($F_g$) minus the viscose force ($F_v$) so that:
| $ F = F_g - F_v $ |
This relation allows establishing the motion equation for the instant acceleration ($a$) with ($$) falling due to Earth's gravity with the gravitational Acceleration ($g$), and with ($$), in the constant of the Viscose Force ($b$), it will take the form of:
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Mass and Density
Equation
The density ($\rho$) is defined as the ratio between the mass ($M$) and the volume ($V$), expressed as:
| $ \rho \equiv\displaystyle\frac{ m_i }{ V }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
This property is specific to the material in question.
ID:(3704, 0)
Sphere volume
Equation
The volume of a sphere ($V$) for a sphere with ($$) is calculated using the following formula:
| $ V =\displaystyle\frac{4 \pi }{3} r ^3$ |
ID:(4445, 0)
Equality of inertial and gravitational mass
Equation
The masses that Newton used in his principles are related to the inertia of bodies, which leads to the concept of the inertial Mass ($m_i$).
Newton's law, which is linked to the force between bodies due to their masses, is related to gravity, hence known as the gravitational mass ($m_g$).
Empirically, it has been concluded that both masses are equivalent, and therefore, we define
| $ m_g = m_i $ |
Einstein was the one who questioned this equality and, from that doubt, understood why both 'appear' equal in his theory of gravity. In his argument, Einstein explained that masses deform space, and this deformation of space causes a change in the behavior of bodies. Thus, masses turn out to be equivalent. The revolutionary concept of space curvature implies that even light, which lacks mass, is affected by celestial bodies, contradicting Newton's theory of gravitation. This was experimentally demonstrated by studying the behavior of light during a solar eclipse. In this situation, light beams are deflected due to the presence of the sun, allowing stars behind it to be observed.
ID:(12552, 0)
Characteristic time of the Stokes equation
Equation
With the Stokes model, the viscous resistance the constant of the Viscose Force ($b$), which depends on the radio de la Gota ($r$) and the environment viscosity ($\eta$), is calculated as:
| $ b \equiv 6 \pi \eta r $ |
This leads to the viscosity time and inertial mass ($\tau_i$) and the viscosity time and gravitational mass ($\tau_g$) assuming equal values the adaptation time ($\tau$), which are calculated with the density ($\rho$) as follows:
| $\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$ |
If the characteristic time is defined as
$\tau=\displaystyle\frac{m_i}{b}$
and the coefficient of viscous force is
$b=6\pi r\eta$
On the other hand, considering that
| $ \rho \equiv\displaystyle\frac{ m_i }{ V }$ |
and
| $ V =\displaystyle\frac{4 \pi }{3} r ^3$ |
it follows that the mass is
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
which leads to
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
in other words,
| $\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$ |
ID:(14465, 0)
Gravitational mass time and viscosity
Equation
With the equation of motion of a body in a viscous medium, we have the derivative of the speed ($v$) at the time ($t$) with the inertial Mass ($m_i$), the gravitational mass ($m_g$), the constant of the Viscose Force ($b$) and the gravitational Acceleration ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This defines the viscosity time and gravitational mass ($\tau_g$) as:
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Horizontal speed in viscous medium
Equation
In the scenario of horizontal motion, the sphere encounters resistance solely from the viscosity of the surrounding medium, which can be quantified by the equation involving the speed ($v$) with the initial Speed ($v_0$), the viscosity time and inertial mass ($\tau_i$), and the time ($t$):
| $ v = v_0 e^{- t / \tau_i }$ |
Consequently, the interaction among these elements leads to the observation that the component x of velocity ($v_x$) with the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
ID:(6844, 0)
Viscous medium horizontal position
Equation
Within the context of horizontal motion, the position is obtained by integrating the velocity, resulting in an equation involving the position ($s$) with the starting position ($s_0$), the initial Speed ($v_0$), the viscosity time and gravitational mass ($\tau_g$), the viscosity time and inertial mass ($\tau_i$), the gravitational Acceleration ($g$), and the time ($t$):
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
From this equation, we arrive at the horizontal displacement equation for the initial position on the x-axis ($x_0$), the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
ID:(14467, 0)
Inertial mass time and viscosity
Equation
With the equation of motion of a body in a viscous medium, we have the derivative of the speed ($v$) at the time ($t$) with the constant of the Viscose Force ($b$) and the gravitational Acceleration ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This defines the viscosity time and inertial mass ($\tau_i$) as:
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Vertical velocity in a viscous medium under gravity
Equation
In the context of vertical motion, the sphere faces a dual resistance: on one hand, the viscosity of the surrounding medium, and on the other, gravity pulling it downward. The latter can be quantified by the equation in the speed ($v$) with the initial Speed ($v_0$), the viscosity time and gravitational mass ($\tau_g$), the viscosity time and inertial mass ($\tau_i$), the gravitational Acceleration ($g$), and the time ($t$):
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Assuming gravitational mass and inertial mass are identical, we obtain the function for the component y of velocity ($v_y$) with the initial vertical speed ($v_{0y}$), the adaptation time ($\tau$), the gravitational Acceleration ($g$), and the time ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
ID:(14466, 0)
Viscous medium vertical position under gravitation
Equation
In the context of vertical motion, the position is obtained by integrating velocity, resulting in an equation involving the position ($s$) with the starting position ($s_0$), the initial Speed ($v_0$), the viscosity time and gravitational mass ($\tau_g$), the viscosity time and inertial mass ($\tau_i$), the gravitational Acceleration ($g$), and the time ($t$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
From this equation, we arrive at the equation for vertical displacement for the position on the y-axis ($y$) with the initial position on the y-axis ($y_0$), the initial horizontal speed ($v_{0x}$), the adaptation time ($\tau$), and the time ($t$):
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
ID:(14468, 0)