Utilisateur: 
Pendule physique
Storyboard 
Dans le cas d'un pendule composé avec une masse réelle, l'énergie potentielle est générée par l'élévation du centre de masse contre le champ gravitationnel à mesure que le pendule se dévie d'un angle donné.
ID:(1421, 0)
Oscillations avec un pendule physique
Description
Contrairement au pendule mathématique, le pendule physique travaille avec une masse réelle, non ponctuelle. Alors que la longueur l est définie comme la distance entre le pivot et le centre de masse du corps, l'énergie potentielle des deux pendules est identique. Cependant, l'énergie cinétique ne peut plus être approximée à l'aide d'expressions dépendant uniquement de l et m; il est nécessaire de connaître le moment d'inertie réel du corps.
ID:(7097, 0)
Pendule physique
Description
Contrairement au pendule mathématique, le pendule physique travaille avec une masse réelle, et non pas ponctuelle. En définissant la longueur l comme la distance entre l'axe et le centre de masse du corps, l'énergie potentielle des deux pendules coïncide. Cependant, l'énergie cinétique ne peut plus être approximée par une expression dépendant uniquement de l et de $m"; elle doit plutôt inclure le moment d'inertie réel du corps.
ID:(1188, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
E = K_r + V
E = K + V
K_r =\displaystyle\frac{1}{2} I \omega ^2
K_r = I * omega ^2/2
\nu =\displaystyle\frac{1}{ T }
nu =1/ T
\omega_0 = 2 \pi \nu
omega = 2* pi * nu
\omega_0 = \displaystyle\frac{2 \pi }{ T }
omega = 2* pi / T
\omega_0 ^2=\displaystyle\frac{ m g L }{ I }
omega_0 ^2 = m * g * L / I
\omega = - \theta_0 \omega_0 \sin \omega_0 t
v = - x_0 * omega_0 *sin( omega_0 * t )
V =\displaystyle\frac{1}{2} m_g g L \theta ^2
V = m_g * g * L * theta ^2/2
E =\displaystyle\frac{1}{2} m_g g L \theta_0 ^2
V = m_g * g * L * theta ^2/2
\theta = \theta_0 \cos \omega_0 t
x = x_0 *cos( omega_0 * t )
ID:(15853, 0)
Énergie totale
Équation
La énergie totale correspond à la somme de l'énergie cinétique totale et de l'énergie potentielle :
| E = K_r + V |
| E = K + V |
ID:(3687, 0)
Énergie cinétique de rotation
Équation
Dans le cas de l'étude de la translation, la définition de l'énergie
| \Delta W = T \Delta\theta |
est appliquée à la deuxième loi de Newton
| T = I \alpha |
ce qui conduit à l'expression
| K_r =\displaystyle\frac{1}{2} I \omega ^2 |
L'énergie nécessaire pour qu'un objet passe de la vitesse angulaire \omega_1 à la vitesse angulaire \omega_2 peut être calculée à l'aide de la définition
| \Delta W = T \Delta\theta |
Avec la deuxième loi de Newton, nous pouvons réécrire cette expression comme
\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta
En utilisant la définition de la vitesse angulaire
| \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t } |
nous obtenons
\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I,\omega,\Delta\omega
La différence entre les vitesses angulaires est
\Delta\omega=\omega_2-\omega_1
D'autre part, la vitesse angulaire elle-même peut être approximée par la vitesse angulaire moyenne
\omega=\displaystyle\frac{\omega_1+\omega_2}{2}
En utilisant ces deux expressions, nous obtenons l'équation
\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)
Ainsi, l'énergie varie selon
\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2
Nous pouvons utiliser cela pour définir l'énergie cinétique
| K_r =\displaystyle\frac{1}{2} I \omega ^2 |
ID:(3255, 0)
Énergie potentielle d'un pendule mathématique pour les petits angles (1)
Équation
L'énergie potentielle gravitationnelle d'un pendule est
| U = m g L (1-\cos \theta ) |
qui peut être approximée pour de petits angles comme :
| V =\displaystyle\frac{1}{2} m_g g L \theta ^2 |
L'énergie potentielle gravitationnelle d'un pendule avec une masse
| U = m g L (1-\cos \theta ) |
où
Pour de petits angles, la fonction cosinus peut être approximée par le développement en série de Taylor jusqu'à l'ordre deux
\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2
Cette approximation conduit à une simplification de l'énergie potentielle en
| V =\displaystyle\frac{1}{2} m_g g L \theta ^2 |
Il est important de noter que l'angle doit être en radians.
ID:(4514, 1)
Énergie potentielle d'un pendule mathématique pour les petits angles (2)
Équation
L'énergie potentielle gravitationnelle d'un pendule est
| U = m g L (1-\cos \theta ) |
qui peut être approximée pour de petits angles comme :
| E =\displaystyle\frac{1}{2} m_g g L \theta_0 ^2 |
| V =\displaystyle\frac{1}{2} m_g g L \theta ^2 |
L'énergie potentielle gravitationnelle d'un pendule avec une masse
| U = m g L (1-\cos \theta ) |
où
Pour de petits angles, la fonction cosinus peut être approximée par le développement en série de Taylor jusqu'à l'ordre deux
\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2
Cette approximation conduit à une simplification de l'énergie potentielle en
| V =\displaystyle\frac{1}{2} m_g g L \theta ^2 |
Il est important de noter que l'angle doit être en radians.
ID:(4514, 2)
Fréquence angulaire pour un pendule physique
Équation
En ce qui concerne le pendule physique:
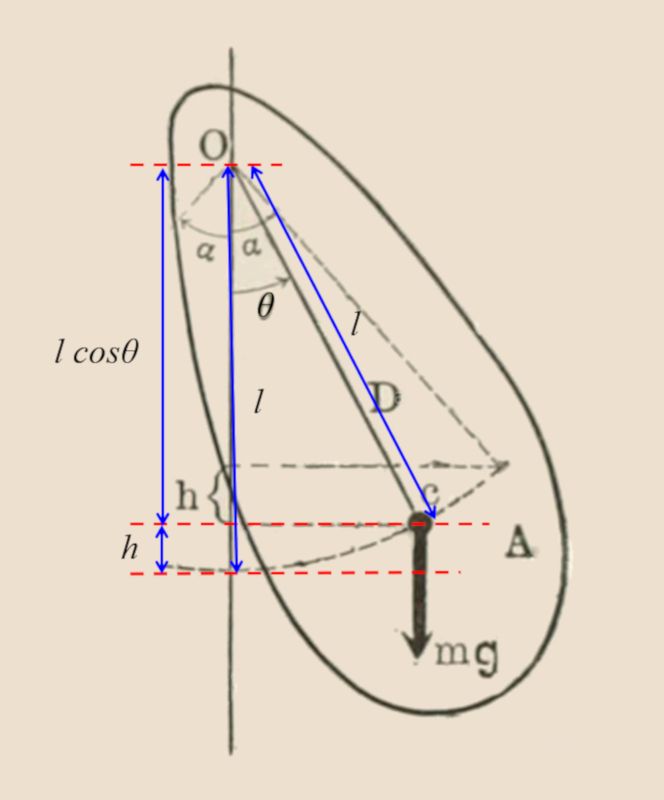
L'énergie est donnée par :
E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2
Par conséquent, la fréquence angulaire est:
| \omega_0 ^2=\displaystyle\frac{ m g L }{ I } |
Étant donné que l'énergie cinétique du pendule physique avec un moment d'inertie I et une vitesse angulaire \omega est représentée par
et l'énergie potentielle gravitationnelle est donnée par
où m est la masse, l est la longueur de la corde, \theta est l'angle et g est l'accélération angulaire, l'équation d'énergie peut être exprimée comme
E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2
Comme la période est définie comme
T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}
nous pouvons déterminer la fréquence angulaire comme suit :
ID:(4517, 0)
Fréquence angulaire
Équation
A fréquence angulaire (\omega) est avec a période (T) égal à
| \omega_0 = \displaystyle\frac{2 \pi }{ T } |
| \omega = \displaystyle\frac{2 \pi }{ T } |
ID:(12335, 0)
Fréquence
Équation
A fréquence (\nu) correspond au nombre de fois qu'une oscillation se produit en une seconde. A période (T) représente le temps nécessaire à une seule oscillation. Par conséquent, le nombre d'oscillations par seconde est :
| \nu =\displaystyle\frac{1}{ T } |
La fréquence est indiquée en Hertz (Hz).
ID:(4427, 0)
Amplitude des oscillations
Équation
Avec la description de l'oscillation à l'aide de
| z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t |
la partie réelle correspond à l'évolution temporelle de l'amplitude
| \theta = \theta_0 \cos \omega_0 t |
| x = x_0 \cos \omega_0 t |
ID:(14074, 0)
Vitesse d'oscillation
Équation
En obtenant la partie réelle de la dérivée du nombre complexe représentant l'oscillation
dont la partie réelle correspond à la vitesse
| \omega = - \theta_0 \omega_0 \sin \omega_0 t |
| v = - x_0 \omega_0 \sin \omega_0 t |
En utilisant le nombre complexe
introduit dans
nous obtenons
\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t
ainsi, la vitesse est obtenue comme la partie réelle
ID:(14076, 0)