Utilisateur: 
Diagramme dans l'espace de position d'impulsion $p-q$
Description 
Une technique d'analyse du mouvement consiste à représenter le moment en fonction de la position d'un corps en déplacement. Cette représentation permet d'étudier comment le moment évolue en fonction de la position atteinte.
La représentation du mouvement dans l'espace moment-position $p-q$ permet d'analyser l'évolution du déplacement en montrant les extrêmes de la position et du moment.
Dans le cas d'un mouvement périodique ou lorsque nous considérons le trajet aller-retour, cela peut être représenté comme ceci :
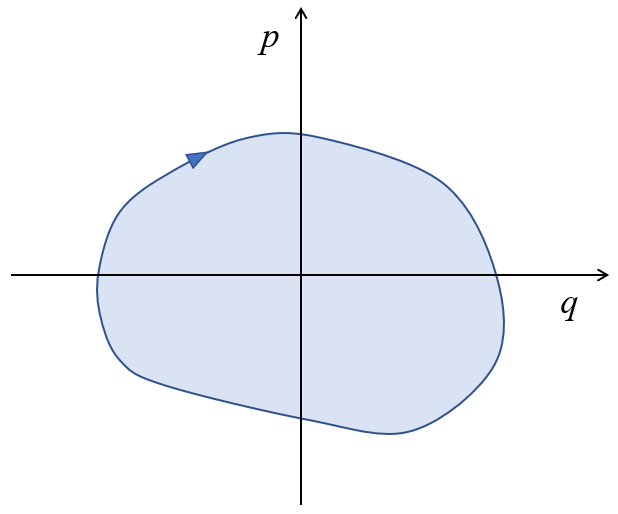
De plus, nous pouvons observer que la zone entourée par la courbe
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
correspond à l'énergie du système.
La zone entourant la courbe sur le diagramme moment-position $p-q$ correspond à l'énergie du système.
ID:(1240, 0)
Énergie cinétique en fonction du moment
Équation
L'énergie cinétique d'une masse $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
peut être exprimée en fonction du moment comme
 $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
Comme l'énergie cinétique est égale à
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
et le moment est
| $ p = m_i v $ |
nous pouvons l'exprimer comme
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
c'est-à-dire
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
ID:(4425, 0)
Moment en fonction de l'énergie et de la fonction potentielle
Équation
Si on isole l'énergie par rapport au moment, on obtient les expressions pour le moment positif et négatif :
| $ p =\pm\sqrt{2 m ( E - U )}$ |
En général, l'énergie est la somme de l'énergie cinétique
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
et de l'énergie potentielle
$E=\displaystyle\frac{p^2}{2m}+U$
En résolvant pour le moment, on obtient l'expression suivante :
| $ p =\pm\sqrt{2 m ( E - U )}$ |
ID:(4429, 0)
Particules sous accélération gravitationnelle dans la représentation $p-q$
Équation
Pour le cas d'une particule dans le champ gravitationnel de la Terre, l'énergie en fonction du moment $p$ et de la position $q$ est
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
Comme l'énergie cinétique en fonction du moment est
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
et l'énergie potentielle en fonction de la hauteur est
| $ V = m_g g z $ |
donc, si on exprime la hauteur comme la position
$h = q$
on obtient
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
L'équation peut être écrite de manière adimensionnelle comme
$y=\pm\sqrt{1-x}$
avec
$x=\displaystyle\frac{q}{mg/E}$
, et
$y=\displaystyle\frac{p}{\sqrt{2mE}}$
ce qui est représenté ci-dessous
ID:(4426, 0)
Oscillateur harmonique (ressort) représentant $p-q$
Équation
Pour le cas d'une masse oscillant avec un ressort, l'énergie en fonction du moment $p$ et de la position $q$ est
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
L'énergie cinétique en fonction du moment est
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
et l'énergie potentielle en fonction de la hauteur est
donc si l'on exprime l'allongement comme la position
$x = q$
nous obtenons
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
L'équation peut être écrite sous forme adimensionnelle comme
$1=y^2 + x^2$
avec
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
, et
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
lorsqu'elle est résolue pour
$y=\pm\sqrt{1-x^2}$
Sa représentation dans le plan xy est montrée ci-dessous
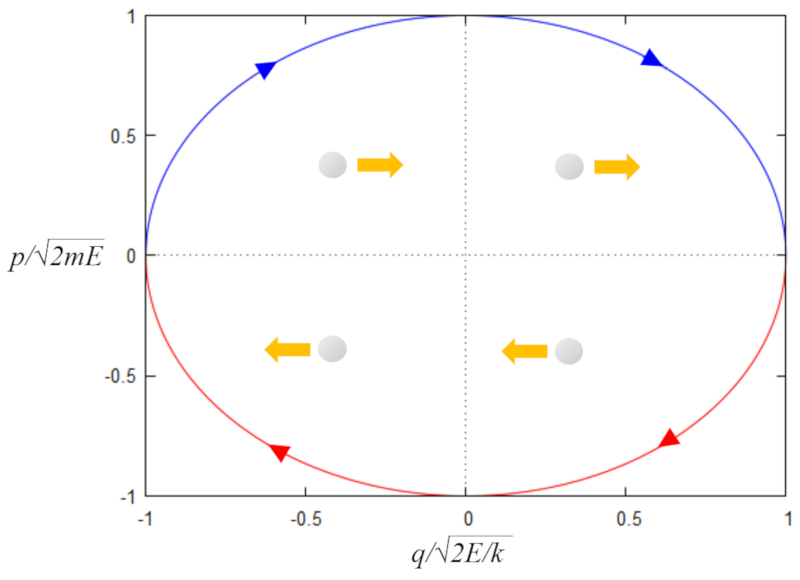
ID:(1187, 0)
Masse dans le champ gravitationnel en représentation en $p-q$
Équation
Pour le cas d'une masse dans un champ gravitationnel, l'énergie en fonction de la quantité de mouvement
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Comme l'énergie cinétique est
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
et l'énergie potentielle est
| $ V = - \displaystyle\frac{ G m M }{ r } $ |
on peut exprimer l'énergie en fonction du rayon représenté par la variable $q$ comme suit
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Dans le cas où l'énergie cinétique dépasse l'énergie potentielle au rayon initial et que l'énergie est positive (indiquant que l'objet peut s'échapper de la planète), l'équation peut être écrite comme
$1 = \left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 - \displaystyle\frac{GmM}{Eq}$
c'est-à-dire,
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
avec
$x=\displaystyle\frac{q}{GmM/E}$
, et
$y=\displaystyle\frac{p}{2mE}$
Dans le cas où l'énergie cinétique ne dépasse pas l'énergie potentielle (indiquant que l'objet ne peut pas échapper à l'attraction de la planète), l'énergie est négative et l'expression est écrite comme
$1 = -\left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 + \displaystyle\frac{GmM}{Eq}$
où $E$ est la valeur absolue de l'énergie, et avec les définitions de $x" et $y", nous avons
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
L'équation peut être exprimée de manière adimensionnelle pour le cas d'une énergie positive, comme les courbes bleues et vertes :
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
Et pour le cas d'une énergie négative, en utilisant les courbes rouges et violettes :
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
Où :
$x=\displaystyle\frac{q}{GmM/E}$
, et
$y=\displaystyle\frac{p}{2mE}$
Tout cela est représenté ci-dessous :
ID:(1185, 0)
0
Video
Vidéo: Espace des phases