User:
Diagram in momentum-position space $p-q$
Description 
An analytical technique to analyze motion involves representing momentum as a function of the position of a moving object. This representation enables us to study how momentum evolves with respect to the achieved position.
The representation of motion in the momentum-position space $p-q$ allows us to analyze the displacement's evolution, highlighting extremes in position and momentum.
In the case of periodic motion or when considering the journey both ways, it can be represented as:
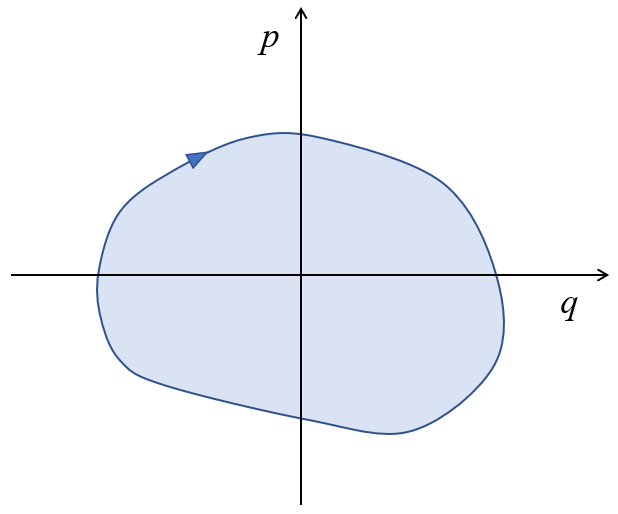
Furthermore, it's evident that the area enclosed by the curve
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
corresponds to the system's energy.
The area enclosed by the curve in the momentum-position diagram $p-q$ corresponds to the system's energy.
ID:(1240, 0)
Kinetic energy as a function of moment
Equation
The kinetic energy of a mass $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
can be expressed in terms of momentum as
 $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
Since kinetic energy is equal to
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
and momentum is
| $ p = m_i v $ |
we can express it as
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
or
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
ID:(4425, 0)
Moment as a function of energy and potential function
Equation
If the energy is solved for the momentum, the expressions for positive and negative momentum are obtained:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
Since in general, energy is the sum of kinetic energy
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
and potential energy
$E=\displaystyle\frac{p^2}{2m}+U$
If we solve for momentum, we get the following expression:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
ID:(4429, 0)
Particle under gravitational acceleration in representation $p-q$
Equation
For the case of a particle in the gravitational field of the Earth, the energy as a function of momentum $p$ and position $q$ is given by
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
As the kinetic energy as a function of momentum is
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
and the potential energy as a function of height is
| $ V = m_g g z $ |
so if the height is expressed as the position
$h = q$
we get
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
The equation can be written in an adimensional form as
$y=\pm\sqrt{1-x}$
with
$x=\displaystyle\frac{q}{mg/E}$
, and
$y=\displaystyle\frac{p}{\sqrt{2mE}}$
which is represented below
ID:(4426, 0)
Harmonic oscillator (spring) representing $p-q$
Equation
For the case of a mass oscillating with a spring, the energy as a function of momentum $p$ and position $q$ is
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
The kinetic energy as a function of momentum is given by
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
and the potential energy as a function of height is
| $ V =\displaystyle\frac{1}{2} k x ^2$ |
So, if we express the elongation as the position
$x = q$
we obtain
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
The equation can be expressed in an adimensional form as
$1=y^2 + x^2$
where
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
, and
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
solving for
$y=\pm\sqrt{1-x^2}$
Its representation in the xy plane is shown below
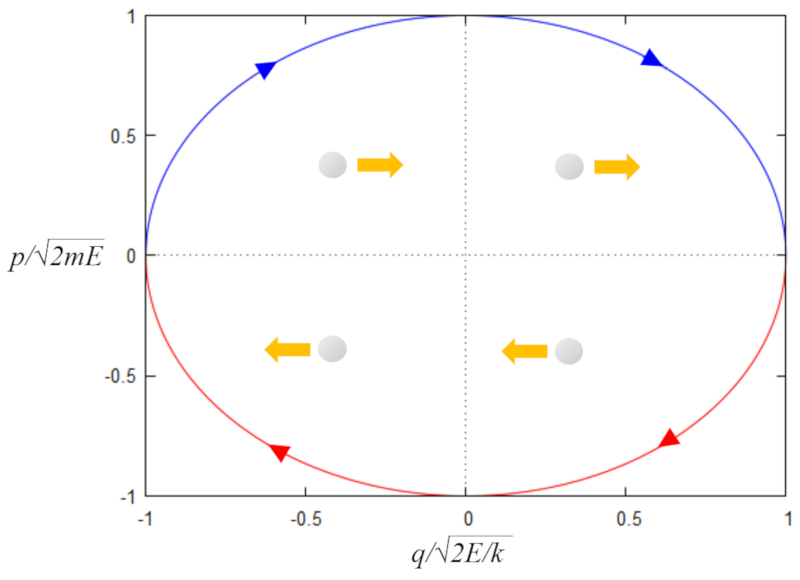
ID:(1187, 0)
Mass in gravitational field in representation in $p-q$
Equation
For the case of a mass in a gravitational field, the energy as a function of momentum
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Given that the kinetic energy is
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
and the potential energy is
| $ V = - \displaystyle\frac{ G m M }{ r } $ |
we can express the energy with the radius denoted by the variable $q$ as
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
In the case where the kinetic energy surpasses the potential energy at the starting radius and the energy is positive (indicating that the object can escape the planet), the equation can be written as
$1 = \left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 - \displaystyle\frac{GmM}{Eq}$
which simplifies to
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
with
$x=\displaystyle\frac{q}{GmM/E}$
, and
$y=\displaystyle\frac{p}{2mE}$
In the case where the kinetic energy does not exceed the potential energy (indicating that the object cannot escape the planet's attraction), the energy is negative, and the expression is written as
$1 = -\left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 + \displaystyle\frac{GmM}{Eq}$
where $E$ is the absolute value of the energy. With the definitions of $x$ and $y$, we then have
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
The equation can be written in an adimensional form for the case of positive energy as (blue and green curves)
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
and for the negative energy case as (red and purple curves)
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
with
$x=\displaystyle\frac{q}{GmM/E}$
, and
$y=\displaystyle\frac{p}{2mE}$
which is depicted below
ID:(1185, 0)
0
Video
Video: Phase Space