Utilizador:
Diagrama no espaço momento-posição $p-q$
Descrição 
Uma técnica para analisar o movimento é representar o momento em função da posição de um corpo em movimento. Essa representação permite estudar como o momento evolui de acordo com a posição alcançada.
A representação do movimento no espaço momento-posição $p-q$ permite analisar a evolução do deslocamento, mostrando extremos na posição e no momento.
No caso de um movimento periódico ou quando consideramos o caminho de ida e volta, isso pode ser representado como:
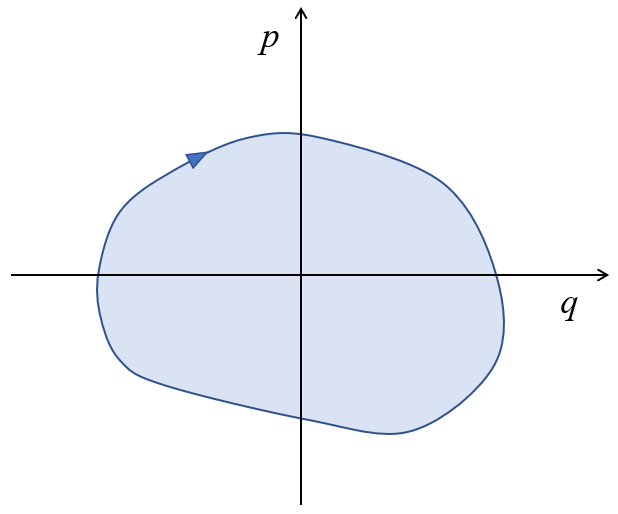
Além disso, podemos observar que a área circundada pela curva
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
corresponde à energia do sistema.
A área circundando a curva no diagrama momento-posição $p-q$ corresponde à energia do sistema.
ID:(1240, 0)
Energia cinética em função do momento
Equação
A energia cinética de uma massa $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
pode ser escrita em termos do momento como
 $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
Como a energia cinética é igual a
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
e o momento é
| $ p = m_i v $ |
podemos expressá-la como
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
ou seja
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
ID:(4425, 0)
Momento em função da energia e função potencial
Equação
Se isolarmos a energia em relação ao momento, obtemos as expressões para o momento positivo e negativo:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
Como geralmente a energia é a soma da energia cinética
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
e da energia potencial
$E=\displaystyle\frac{p^2}{2m}+U$
Quando resolvemos para o momento, obtemos a seguinte expressão:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
ID:(4429, 0)
Partícula sob aceleração gravitacional na representação $p-q$
Equação
Para o caso de uma partícula no campo gravitacional da Terra, a energia em função do momento $p$ e posição $q$ é
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
Como a energia cinética em função do momento é
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
e a energia potencial em função da altura é
| $ V = m_g g z $ |
portanto, se expressarmos a altura como a posição
$h = q$
obtemos
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
A equação pode ser escrita de forma adimensional como
$y=\pm\sqrt{1-x}$
com
$x=\displaystyle\frac{q}{mg/E}$
, e
$y=\displaystyle\frac{p}{\sqrt{2mE}}$
que é representada abaixo
ID:(4426, 0)
Oscilador harmônico (mola) representando $p-q$
Equação
Para o caso de uma massa oscilando com uma mola, a energia em função do momento $p$ e da posição $q$ é
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
A energia cinética em função do momento é
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
e a energia potencial em função da altura é
portanto, se expressarmos a elongação como a posição
$x = q$
obtemos
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
A equação pode ser escrita de forma adimensional como
$1=y^2 + x^2$
com
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
, e
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
quando resolvido para
$y=\pm\sqrt{1-x^2}$
Sua representação no plano xy é mostrada abaixo
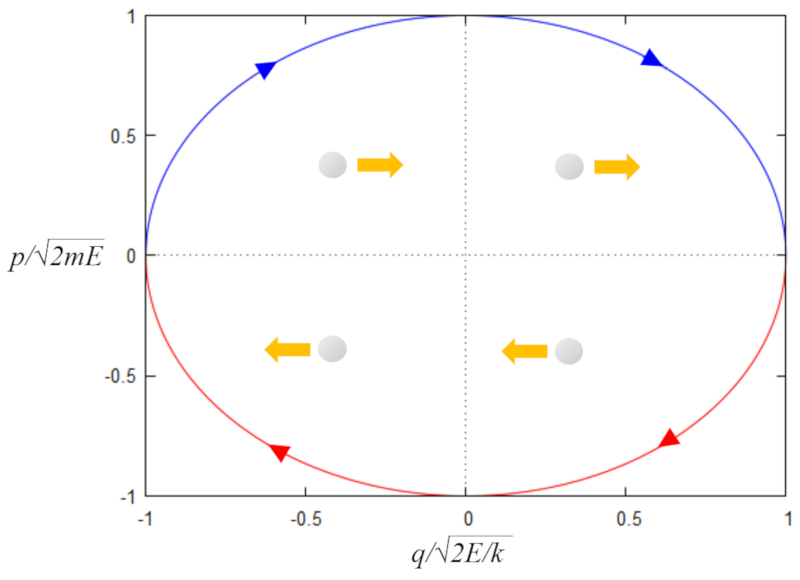
ID:(1187, 0)
Massa no campo gravitacional em representação em $p-q$
Equação
Para o caso de uma massa no campo gravitacional, a energia em função do momento
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Como a energia cinética é
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
e a energia potencial é
| $ V = - \displaystyle\frac{ G m M }{ r } $ |
podemos expressar a energia em função do raio representado pela variável $q$ da seguinte forma
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
No caso em que a energia cinética supera a energia potencial no raio inicial e a energia é positiva (indicando que o objeto pode escapar do planeta), a equação pode ser escrita como
$1 = \left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 - \displaystyle\frac{GmM}{Eq}$
ou seja,
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
com
$x=\displaystyle\frac{q}{GmM/E}$
, e
$y=\displaystyle\frac{p}{2mE}$
No caso em que a energia cinética não supera a energia potencial (indicando que o objeto não pode escapar da atração do planeta), a energia é negativa e a expressão é escrita como
$1 = -\left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 + \displaystyle\frac{GmM}{Eq}$
onde $E$ é o valor absoluto da energia, e com as definições de $x$ e $y", temos
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
A equação pode ser escrita de forma adimensional para o caso de energia positiva, como as curvas azul e verde:
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
E para o caso de energia negativa, usando as curvas vermelha e violeta:
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
Onde:
$x=\displaystyle\frac{q}{GmM/E}$
, e
$y=\displaystyle\frac{p}{2mE}$
Tudo isso é representado abaixo:
ID:(1185, 0)
0
Video
Vídeo: Espaço de Fase