Interception à accélération angulaire constante
Storyboard 
Les objets peuvent se croiser lorsqu'ils coïncident à un même angle au même instant. Pour y parvenir, ils doivent se déplacer depuis leurs angles et vitesses angulaires initiaux respectifs avec des accélérations angulaires qui leur permettent de coïncider en angle et en temps à la fin du trajet.
ID:(1451, 0)
Evolution de l'angle des corps
Citation 
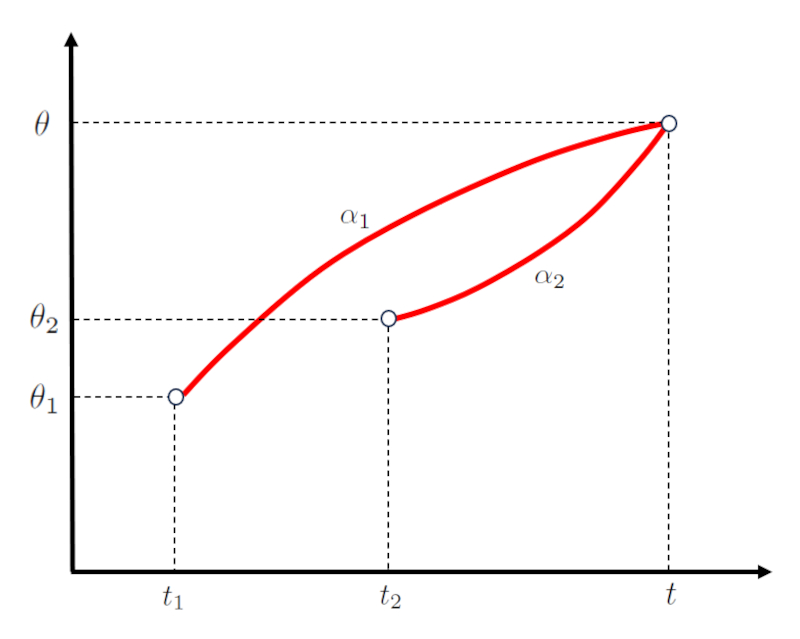
Dans le cas d'un mouvement de deux corps, l'angle auquel la trajectoire du premier se termine coïncide avec celui du deuxième corps à A angle d'intersection ($\theta$).
De même, le moment où la trajectoire du premier se termine coïncide avec celui du deuxième corps à Le temps d'intersection ($t$).
Pour le premier corps, a angle d'intersection ($\theta$) dépend de le angle initial du premier corps ($\theta_1$), a vitesse angulaire initiale du premier corps ($\omega_{01}$), a accélération angulaire du premier corps ($\alpha_1$), le heure initiale du premier objet ($t_1$), comme suit :
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
Tandis que pour le deuxième corps, a angle d'intersection ($\theta$) dépend de le angle initial du deuxième corps ($\theta_2$), a vitesse angulaire initiale du deuxième corps ($\omega_{02}$), a accélération angulaire du deuxième corps ($\alpha_2$), le temps initial du deuxième objet ($t_2$), comme suit :
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Ceci est représenté comme suit :
ID:(12514, 0)
Interception à accélération angulaire constante
Description 
Les objets peuvent se croiser lorsqu'ils coïncident à un même angle au même instant. Pour y parvenir, ils doivent se déplacer depuis leurs angles et vitesses angulaires initiaux respectifs avec des accélérations angulaires qui leur permettent de coïncider en angle et en temps à la fin du trajet.
Variables
Calculs
Calculs
Équations
La d finition de l'acc l ration angulaire moyenne repose sur l'angle parcouru
| $ \Delta\omega = \omega_2 - \omega_1 $ |
et le temps coul
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme l'acc l ration angulaire moyenne
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
pendant cet intervalle de temps.
(ID 3234)
La d finition de l'acc l ration angulaire moyenne repose sur l'angle parcouru
| $ \Delta\omega = \omega_2 - \omega_1 $ |
et le temps coul
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme l'acc l ration angulaire moyenne
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
pendant cet intervalle de temps.
(ID 3234)
tant donn que a accélération moyenne ($\bar{a}$) est gal a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$) selon
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
et que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) conform ment
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
il en d coule que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
En supposant que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a accélération angulaire constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
et en supposant que a accélération moyenne ($\bar{a}$) est gal a accélération constante ($a_0$)
| $ a_0 = \bar{a} $ |
on obtient l' quation suivante :
| $ a = r \alpha $ |
(ID 3236)
tant donn que a accélération moyenne ($\bar{a}$) est gal a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$) selon
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
et que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a différence de vitesses angulaires ($\Delta\omega$) et le temps écoulé ($\Delta t$) conform ment
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
il en d coule que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
En supposant que a accélération angulaire moyenne ($\bar{\alpha}$) est gal a accélération angulaire constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
et en supposant que a accélération moyenne ($\bar{a}$) est gal a accélération constante ($a_0$)
| $ a_0 = \bar{a} $ |
on obtient l' quation suivante :
| $ a = r \alpha $ |
(ID 3236)
Si nous supposons que a accélération angulaire moyenne ($\bar{\alpha}$) est constant, quivalent a accélération angulaire constante ($\alpha_0$), alors l' quation suivante s'applique :
| $ \bar{\alpha} = \alpha_0 $ |
Par cons quent, en consid rant a différence de vitesses angulaires ($\Delta\omega$) avec a vitesse angulaire ($\omega$) et a vitesse angulaire initiale ($\omega_0$) :
| $ \Delta\omega = \omega_2 - \omega_1 $ |
et le temps écoulé ($\Delta t$) en relation avec le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
l' quation pour a accélération angulaire moyenne ($\bar{\alpha}$) :
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
peut tre exprim e comme suit :
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
En r solvant cela, nous obtenons :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Si nous supposons que a accélération angulaire moyenne ($\bar{\alpha}$) est constant, quivalent a accélération angulaire constante ($\alpha_0$), alors l' quation suivante s'applique :
| $ \bar{\alpha} = \alpha_0 $ |
Par cons quent, en consid rant a différence de vitesses angulaires ($\Delta\omega$) avec a vitesse angulaire ($\omega$) et a vitesse angulaire initiale ($\omega_0$) :
| $ \Delta\omega = \omega_2 - \omega_1 $ |
et le temps écoulé ($\Delta t$) en relation avec le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
l' quation pour a accélération angulaire moyenne ($\bar{\alpha}$) :
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
peut tre exprim e comme suit :
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
En r solvant cela, nous obtenons :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Dans le cas de a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) en fonction de le temps ($t$) suit une relation lin aire avec le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) sous la forme :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
tant donn que le d placement angulaire est gal l'aire sous la courbe de vitesse angulaire-temps, dans ce cas, on peut ajouter les contributions du rectangle :
$\omega_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Cela nous m ne l'expression pour le angle ($\theta$) et le angle de départ ($\theta_0$) :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Dans le cas de a accélération angulaire constante ($\alpha_0$), a vitesse angulaire ($\omega$) en fonction de le temps ($t$) suit une relation lin aire avec le temps initial ($t_0$) et a vitesse angulaire initiale ($\omega_0$) sous la forme :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
tant donn que le d placement angulaire est gal l'aire sous la courbe de vitesse angulaire-temps, dans ce cas, on peut ajouter les contributions du rectangle :
$\omega_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Cela nous m ne l'expression pour le angle ($\theta$) et le angle de départ ($\theta_0$) :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Si nous r solvons le temps dans l' quation de a vitesse angulaire ($\omega$) qui inclut les variables a vitesse angulaire initiale ($\omega_0$), le temps ($t$), le temps initial ($t_0$) et a accélération angulaire constante ($\alpha_0$) :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
nous obtenons l'expression suivante pour le temps :
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Cette solution peut tre substitu e dans l' quation pour calculer le angle ($\theta$) en utilisant le angle de départ ($\theta_0$) de la mani re suivante :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
ce qui donne la formule suivante :
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Si nous r solvons le temps dans l' quation de a vitesse angulaire ($\omega$) qui inclut les variables a vitesse angulaire initiale ($\omega_0$), le temps ($t$), le temps initial ($t_0$) et a accélération angulaire constante ($\alpha_0$) :
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
nous obtenons l'expression suivante pour le temps :
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Cette solution peut tre substitu e dans l' quation pour calculer le angle ($\theta$) en utilisant le angle de départ ($\theta_0$) de la mani re suivante :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
ce qui donne la formule suivante :
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Exemples
(ID 15416)
Dans un sc nario de mouvement impliquant deux corps, le premier modifie a différence de vitesse angulaire du premier corps ($\Delta\omega_1$) pendant a temps de trajet du premier objet ($\Delta t_1$) avec a accélération angulaire du premier corps ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
Par la suite, le deuxi me corps avance, modifiant a différence de vitesse angulaire du deuxième corps ($\Delta\omega_2$) pendant a temps de trajet du deuxième objet ($\Delta t_2$) avec a accélération angulaire du deuxième corps ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Repr sent graphiquement, nous obtenons un diagramme de vitesse et de temps comme illustr ci-dessous :
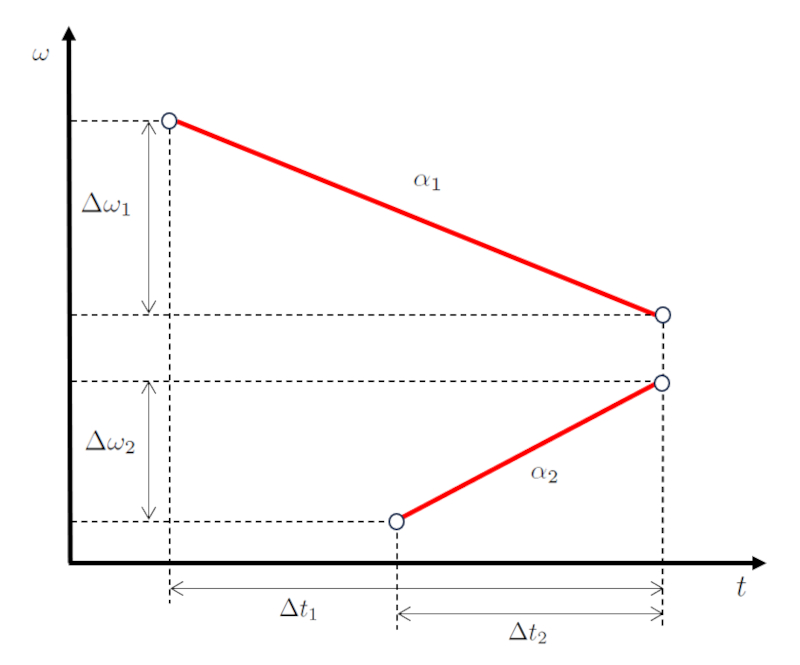
La cl ici est que les valeurs a différence de vitesse angulaire du premier corps ($\Delta\omega_1$) et a différence de vitesse angulaire du deuxième corps ($\Delta\omega_2$), et les valeurs a temps de trajet du premier objet ($\Delta t_1$) et a temps de trajet du deuxième objet ($\Delta t_2$), sont telles que les deux corps co ncident en angle et en temps.
(ID 10579)
Dans le cas de deux corps, le mouvement du premier peut tre d crit par une fonction impliquant les points a vitesse angulaire initiale du premier corps ($\omega_{01}$), a vitesse angulaire finale du premier corps ($\omega_1$), le temps d'intersection ($t$) et le heure initiale du premier objet ($t_1$), repr sent e par une droite avec une pente de a accélération angulaire du premier corps ($\alpha_1$) :
| $ \omega_1 = \omega_{01} + \alpha_1 ( t - t_1 )$ |
Pour le mouvement du deuxi me corps, d fini par les points a vitesse angulaire initiale du deuxième corps ($\omega_{02}$), a vitesse angulaire finale du deuxième corps ($\omega_2$), le temps initial du deuxième objet ($t_2$) et le temps d'intersection ($t$), une deuxi me droite avec une pente de a accélération angulaire du deuxième corps ($\alpha_2$) est utilis e :
| $ \omega_2 = \omega_{02} + \alpha_2 ( t - t_2 )$ |
Ceci est repr sent comme suit :
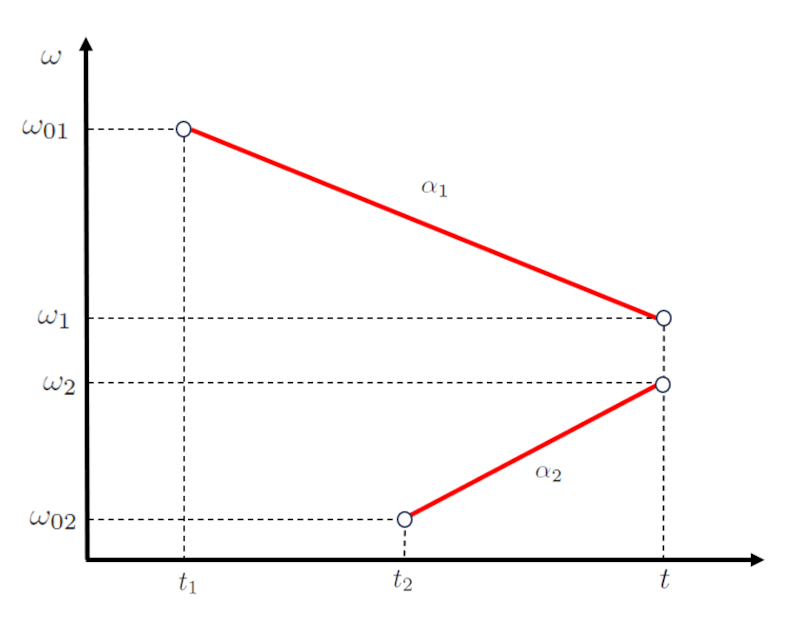
(ID 9872)
Dans le cas d'un mouvement de deux corps, l'angle auquel la trajectoire du premier se termine co ncide avec celui du deuxi me corps a angle d'intersection ($\theta$).
De m me, le moment o la trajectoire du premier se termine co ncide avec celui du deuxi me corps le temps d'intersection ($t$).
Pour le premier corps, a angle d'intersection ($\theta$) d pend de le angle initial du premier corps ($\theta_1$), a vitesse angulaire initiale du premier corps ($\omega_{01}$), a accélération angulaire du premier corps ($\alpha_1$), le heure initiale du premier objet ($t_1$), comme suit :
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
Tandis que pour le deuxi me corps, a angle d'intersection ($\theta$) d pend de le angle initial du deuxième corps ($\theta_2$), a vitesse angulaire initiale du deuxième corps ($\omega_{02}$), a accélération angulaire du deuxième corps ($\alpha_2$), le temps initial du deuxième objet ($t_2$), comme suit :
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Ceci est repr sent comme suit :

(ID 12514)
(ID 15427)
ID:(1451, 0)
