Intercept at constant angular acceleration
Storyboard 
The objects can intersect when they coincide in angle at the same instant. To achieve this, they must move from their respective initial angles and angular velocities with angular accelerations that allow them to coincide in angle and time at the end of the journey.
ID:(1451, 0)
Evolution of the angle of the bodies
Quote 
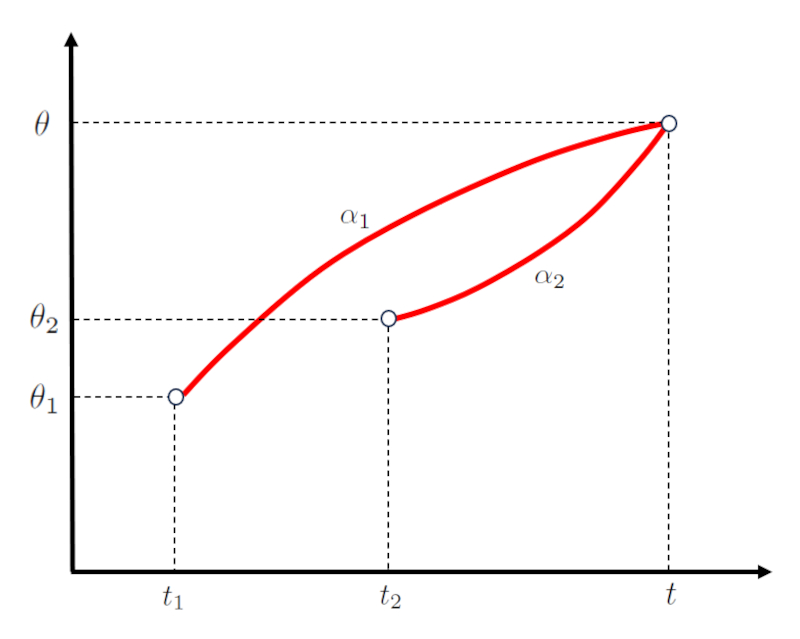
In the case of a two-body motion, the angle at which the trajectory of the first ends coincides with that of the second body at the angle of intersection ($\theta$).
Similarly, the time at which the trajectory of the first ends coincides with that of the second body at the intersection time ($t$).
For the first body, the angle of intersection ($\theta$) depends on the initial angle of the first body ($\theta_1$), the initial angular velocity of the first body ($\omega_{01}$), the angular acceleration of the first body ($\alpha_1$), the initial time of first object ($t_1$), as follows:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
While for the second body, the angle of intersection ($\theta$) depends on the initial angle of the second body ($\theta_2$), the initial angular velocity of the second body ($\omega_{02}$), the angular acceleration of the second body ($\alpha_2$), the initial time of second object ($t_2$), as follows:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
This is represented as:
ID:(12514, 0)
Intercept at constant angular acceleration
Description 
The objects can intersect when they coincide in angle at the same instant. To achieve this, they must move from their respective initial angles and angular velocities with angular accelerations that allow them to coincide in angle and time at the end of the journey.
Variables
Calculations
Calculations
Equations
The definition of average angular acceleration is based on the angle covered
| $ \Delta\omega = \omega_2 - \omega_1 $ |
and the elapsed time
| $ \Delta t \equiv t - t_0 $ |
The relationship between the two is defined as the average angular acceleration
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
within that time interval.
(ID 3234)
The definition of average angular acceleration is based on the angle covered
| $ \Delta\omega = \omega_2 - \omega_1 $ |
and the elapsed time
| $ \Delta t \equiv t - t_0 $ |
The relationship between the two is defined as the average angular acceleration
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
within that time interval.
(ID 3234)
Given that the mean Acceleration ($\bar{a}$) equals the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$) according to
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
and the mean Angular Acceleration ($\bar{\alpha}$) equals the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$) as per
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
it follows that
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assuming that the mean Angular Acceleration ($\bar{\alpha}$) is equal to the constant Angular Acceleration ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
and assuming that the mean Acceleration ($\bar{a}$) equals the constant Acceleration ($a_0$)
| $ a_0 = \bar{a} $ |
then the following equation is obtained:
| $ a = r \alpha $ |
(ID 3236)
Given that the mean Acceleration ($\bar{a}$) equals the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$) according to
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
and the mean Angular Acceleration ($\bar{\alpha}$) equals the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$) as per
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
it follows that
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assuming that the mean Angular Acceleration ($\bar{\alpha}$) is equal to the constant Angular Acceleration ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
and assuming that the mean Acceleration ($\bar{a}$) equals the constant Acceleration ($a_0$)
| $ a_0 = \bar{a} $ |
then the following equation is obtained:
| $ a = r \alpha $ |
(ID 3236)
If we assume that the mean Angular Acceleration ($\bar{\alpha}$) is constant, equivalent to the constant Angular Acceleration ($\alpha_0$), then the following equation applies:
| $ \bar{\alpha} = \alpha_0 $ |
Therefore, considering the difference in Angular Speeds ($\Delta\omega$) along with the angular Speed ($\omega$) and the initial Angular Speed ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
and the time elapsed ($\Delta t$) in relation to the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
the equation for the mean Angular Acceleration ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
can be expressed as:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Solving this, we obtain:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
If we assume that the mean Angular Acceleration ($\bar{\alpha}$) is constant, equivalent to the constant Angular Acceleration ($\alpha_0$), then the following equation applies:
| $ \bar{\alpha} = \alpha_0 $ |
Therefore, considering the difference in Angular Speeds ($\Delta\omega$) along with the angular Speed ($\omega$) and the initial Angular Speed ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
and the time elapsed ($\Delta t$) in relation to the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
the equation for the mean Angular Acceleration ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
can be expressed as:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Solving this, we obtain:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
In the case of the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) as a function of the time ($t$) follows a linear relationship with the start Time ($t_0$) and the initial Angular Speed ($\omega_0$) in the form of:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Given that the angular displacement is equal to the area under the angular velocity-time curve, in this case, one can add the contributions of the rectangle:
$\omega_0(t-t_0)$
and the triangle:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
This leads us to the expression for the angle ($\theta$) and the initial Angle ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
In the case of the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) as a function of the time ($t$) follows a linear relationship with the start Time ($t_0$) and the initial Angular Speed ($\omega_0$) in the form of:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Given that the angular displacement is equal to the area under the angular velocity-time curve, in this case, one can add the contributions of the rectangle:
$\omega_0(t-t_0)$
and the triangle:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
This leads us to the expression for the angle ($\theta$) and the initial Angle ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
If we solve for time in the equation of the angular Speed ($\omega$) that includes the variables the initial Angular Speed ($\omega_0$), the time ($t$), the start Time ($t_0$), and the constant Angular Acceleration ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
we obtain the following expression for time:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
This solution can be substituted into the equation to calculate the angle ($\theta$) using the initial Angle ($\theta_0$) as follows:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
which results in the following equation:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
If we solve for time in the equation of the angular Speed ($\omega$) that includes the variables the initial Angular Speed ($\omega_0$), the time ($t$), the start Time ($t_0$), and the constant Angular Acceleration ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
we obtain the following expression for time:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
This solution can be substituted into the equation to calculate the angle ($\theta$) using the initial Angle ($\theta_0$) as follows:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
which results in the following equation:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Examples
(ID 15416)
In a scenario of two-body motion, the first one alters the angular velocity difference of the first body ($\Delta\omega_1$) during the travel time of first object ($\Delta t_1$) with the angular acceleration of the first body ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
Subsequently, the second body advances, altering the angular velocity difference of the second body ($\Delta\omega_2$) during the travel time of second object ($\Delta t_2$) with the angular acceleration of the second body ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Graphically represented, we obtain a velocity-time diagram as shown below:
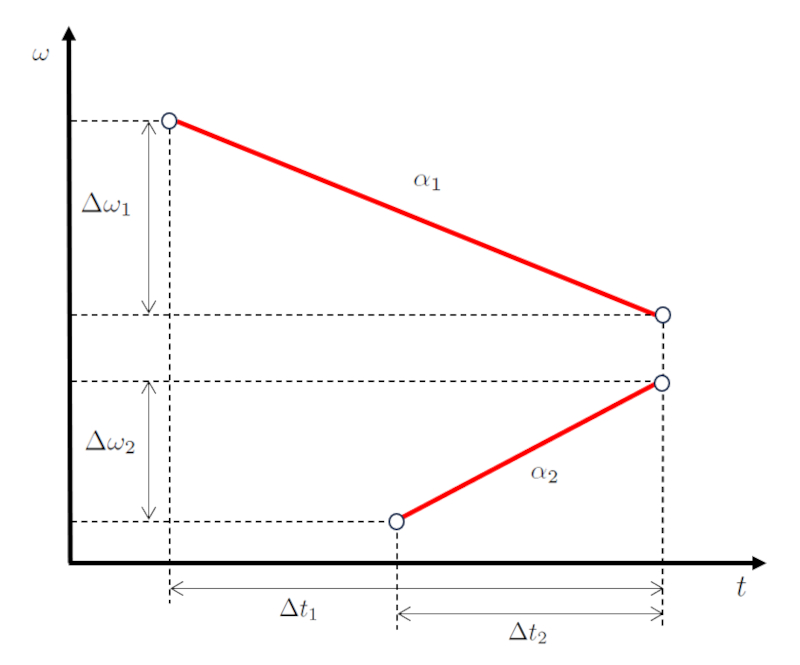
The key here is that the values the angular velocity difference of the first body ($\Delta\omega_1$) and the angular velocity difference of the second body ($\Delta\omega_2$), and the values the travel time of first object ($\Delta t_1$) and the travel time of second object ($\Delta t_2$), are such that both bodies coincide in angle and time.
(ID 10579)
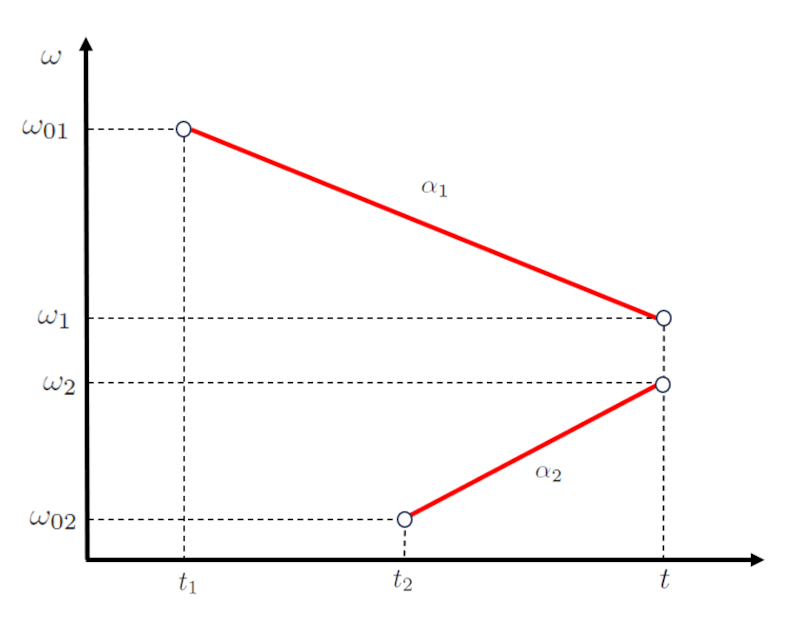
In the case of two bodies, the motion of the first can be described by a function involving the points the initial angular velocity of the first body ($\omega_{01}$), the final angular velocity of the first body ($\omega_1$), the intersection time ($t$), and the initial time of first object ($t_1$), represented by a line with a slope of the angular acceleration of the first body ($\alpha_1$):
| $ \omega_1 = \omega_{01} + \alpha_1 ( t - t_1 )$ |
For the motion of the second body, defined by the points the initial angular velocity of the second body ($\omega_{02}$), the final angular velocity of the second body ($\omega_2$), the initial time of second object ($t_2$), and the intersection time ($t$), a second line with a slope of the angular acceleration of the second body ($\alpha_2$) is utilized:
| $ \omega_2 = \omega_{02} + \alpha_2 ( t - t_2 )$ |
This is represented as:
(ID 9872)
In the case of a two-body motion, the angle at which the trajectory of the first ends coincides with that of the second body at the angle of intersection ($\theta$).
Similarly, the time at which the trajectory of the first ends coincides with that of the second body at the intersection time ($t$).
For the first body, the angle of intersection ($\theta$) depends on the initial angle of the first body ($\theta_1$), the initial angular velocity of the first body ($\omega_{01}$), the angular acceleration of the first body ($\alpha_1$), the initial time of first object ($t_1$), as follows:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
While for the second body, the angle of intersection ($\theta$) depends on the initial angle of the second body ($\theta_2$), the initial angular velocity of the second body ($\omega_{02}$), the angular acceleration of the second body ($\alpha_2$), the initial time of second object ($t_2$), as follows:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
This is represented as:

(ID 12514)
(ID 15427)
ID:(1451, 0)
