Interceptar a aceleración angular constante
Storyboard 
Los objetos pueden cruzarse cuando coinciden en el ángulo en el mismo instante. Para lograrlo, deben moverse desde sus respectivos ángulos y velocidades angulares iniciales con aceleraciones angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
ID:(1451, 0)
Evolución del angulo de los cuerpos
Cita 
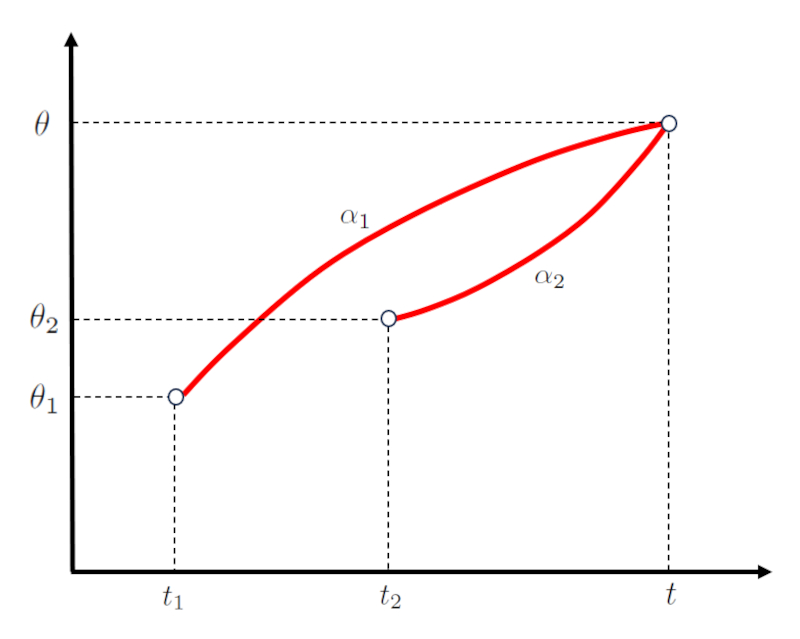
En el caso de un movimiento de dos cuerpos, el ángulo en el que termina la trayectoria del primero coincide con el del segundo cuerpo en la ángulo de la intersección ($\theta$).
Del mismo modo, el tiempo en el que termina la trayectoria del primero coincide con el del segundo cuerpo en el tiempo de intersección ($t$).
Para el primer cuerpo, la ángulo de la intersección ($\theta$) depende de el ángulo inicial del primer cuerpo ($\theta_1$), la velocidad angular inicial del primer cuerpo ($\omega_{01}$), la aceleración angular del primer cuerpo ($\alpha_1$), el tiempo inicial del primer objeto ($t_1$), como sigue:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
Mientras que para el segundo cuerpo, la ángulo de la intersección ($\theta$) depende de el ángulo inicial del segundo cuerpo ($\theta_2$), la velocidad angular inicial del segundo cuerpo ($\omega_{02}$), la aceleración angular del segundo cuerpo ($\alpha_2$), el tiempo inicial del segundo objeto ($t_2$), como sigue:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Esto se representa como:
ID:(12514, 0)
Interceptar a aceleración angular constante
Descripción 
Los objetos pueden cruzarse cuando coinciden en el ángulo en el mismo instante. Para lograrlo, deben moverse desde sus respectivos ángulos y velocidades angulares iniciales con aceleraciones angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
Variables
Cálculos
Cálculos
Ecuaciones
La aceleraci n angular media se define como la proporci n del ngulo recorrido
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relaci n entre ambos se establece como la aceleraci n angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
(ID 3234)
La aceleraci n angular media se define como la proporci n del ngulo recorrido
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relaci n entre ambos se establece como la aceleraci n angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
(ID 3234)
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) seg n
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuaci n:
| $ a = r \alpha $ |
(ID 3236)
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) seg n
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuaci n:
| $ a = r \alpha $ |
(ID 3236)
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuaci n:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido ($\Delta t$) en relaci n con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuaci n para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta ltima, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuaci n:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido ($\Delta t$) en relaci n con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuaci n para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta ltima, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en funci n de el tiempo ($t$) sigue una relaci n lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ngulo recorrido es igual al rea bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribuci n del rect ngulo:
$\omega_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresi n para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en funci n de el tiempo ($t$) sigue una relaci n lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ngulo recorrido es igual al rea bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribuci n del rect ngulo:
$\omega_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresi n para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Si resolvemos la ecuaci n de la velocidad angular ($\omega$) en t rminos de tiempo, que incluye las variables la velocidad angular inicial ($\omega_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la aceleración angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtenemos la siguiente expresi n para el tiempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta soluci n puede ser sustituida en la ecuaci n para calcular el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$) de la siguiente manera:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Lo que resulta en la siguiente ecuaci n:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Si resolvemos la ecuaci n de la velocidad angular ($\omega$) en t rminos de tiempo, que incluye las variables la velocidad angular inicial ($\omega_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la aceleración angular constante ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
obtenemos la siguiente expresi n para el tiempo:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Esta soluci n puede ser sustituida en la ecuaci n para calcular el ángulo ($\theta$) utilizando el ángulo inicial ($\theta_0$) de la siguiente manera:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Lo que resulta en la siguiente ecuaci n:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Ejemplos
(ID 15416)
En un escenario de movimiento de dos cuerpos, el primero modifica su la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) durante la duración del viaje del primer objeto ($\Delta t_1$) con la aceleración angular del primer cuerpo ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
Posteriormente, el segundo cuerpo avanza, modificando su la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$) durante la duración de viaje del segundo objeto ($\Delta t_2$) con la aceleración angular del segundo cuerpo ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Representado gr ficamente, obtenemos un diagrama de velocidad y tiempo como se muestra a continuaci n:
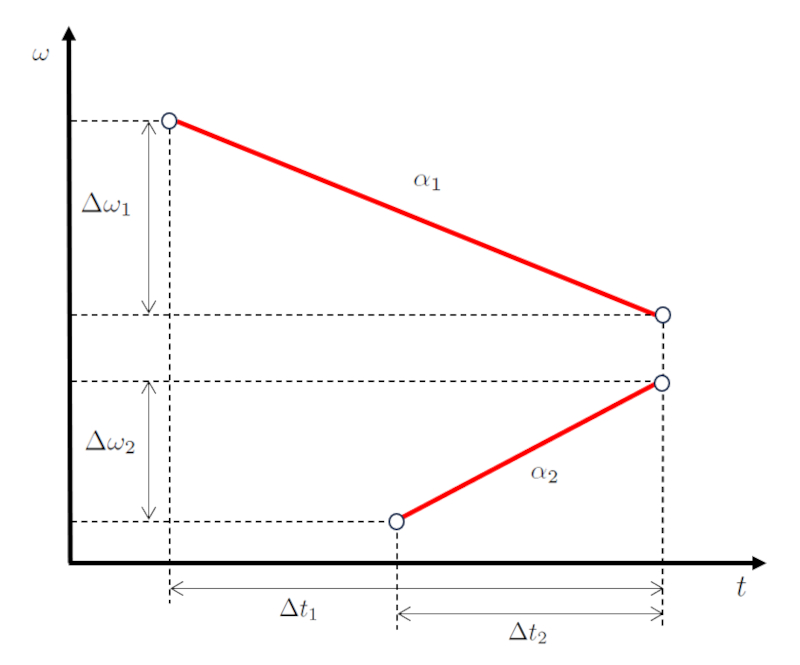
La clave aqu es que los valores la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) y la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$), y los valores la duración del viaje del primer objeto ($\Delta t_1$) y la duración de viaje del segundo objeto ($\Delta t_2$), son tales que ambos cuerpos coinciden en el ngulo y en el tiempo.
(ID 10579)
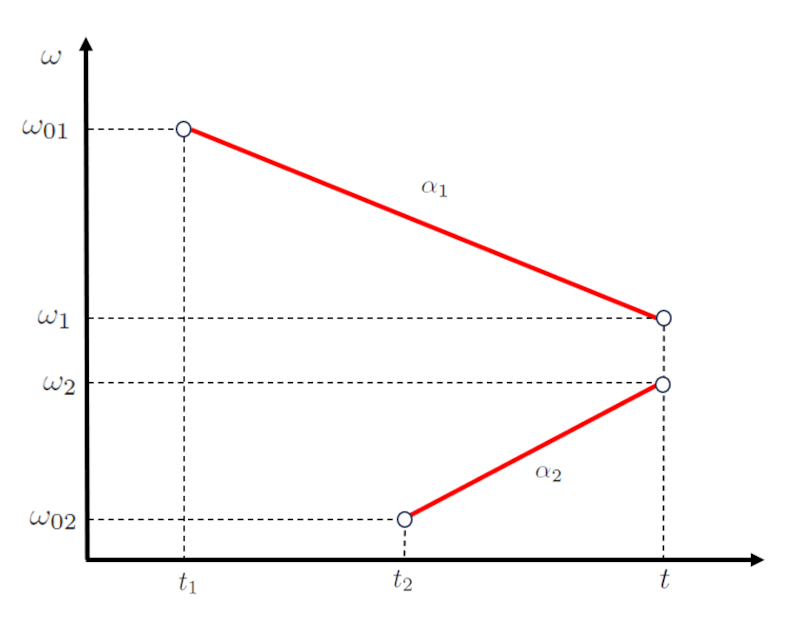
En el caso de dos cuerpos, el movimiento del primero puede describirse mediante una funci n que involucra los puntos la velocidad angular inicial del primer cuerpo ($\omega_{01}$), la velocidad angular final del primer cuerpo ($\omega_1$), el tiempo de intersección ($t$) y el tiempo inicial del primer objeto ($t_1$), representada por una recta con una pendiente de la aceleración angular del primer cuerpo ($\alpha_1$):
| $ \omega_1 = \omega_{01} + \alpha_1 ( t - t_1 )$ |
Para el movimiento del segundo cuerpo, definido por los puntos la velocidad angular inicial del segundo cuerpo ($\omega_{02}$), la velocidad angular final del segundo cuerpo ($\omega_2$), el tiempo inicial del segundo objeto ($t_2$) y el tiempo de intersección ($t$), se utiliza una segunda recta con una pendiente de la aceleración angular del segundo cuerpo ($\alpha_2$):
| $ \omega_2 = \omega_{02} + \alpha_2 ( t - t_2 )$ |
Esto se representa de la siguiente manera:
(ID 9872)
En el caso de un movimiento de dos cuerpos, el ngulo en el que termina la trayectoria del primero coincide con el del segundo cuerpo en la ángulo de la intersección ($\theta$).
Del mismo modo, el tiempo en el que termina la trayectoria del primero coincide con el del segundo cuerpo en el tiempo de intersección ($t$).
Para el primer cuerpo, la ángulo de la intersección ($\theta$) depende de el ángulo inicial del primer cuerpo ($\theta_1$), la velocidad angular inicial del primer cuerpo ($\omega_{01}$), la aceleración angular del primer cuerpo ($\alpha_1$), el tiempo inicial del primer objeto ($t_1$), como sigue:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
Mientras que para el segundo cuerpo, la ángulo de la intersección ($\theta$) depende de el ángulo inicial del segundo cuerpo ($\theta_2$), la velocidad angular inicial del segundo cuerpo ($\omega_{02}$), la aceleración angular del segundo cuerpo ($\alpha_2$), el tiempo inicial del segundo objeto ($t_2$), como sigue:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Esto se representa como:

(ID 12514)
(ID 15427)
ID:(1451, 0)
