Schnittpunkt bei konstanter Winkelbeschleunigung
Storyboard 
Die Objekte können sich kreuzen, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen anfänglichen Winkeln und Winkelgeschwindigkeiten mit Winkelbeschleunigungen bewegen, die es ihnen ermöglichen, am Ende der Reise im Winkel und zur gleichen Zeit übereinzustimmen.
ID:(1451, 0)
Entwicklung des Winkels der Körper
Zitat 
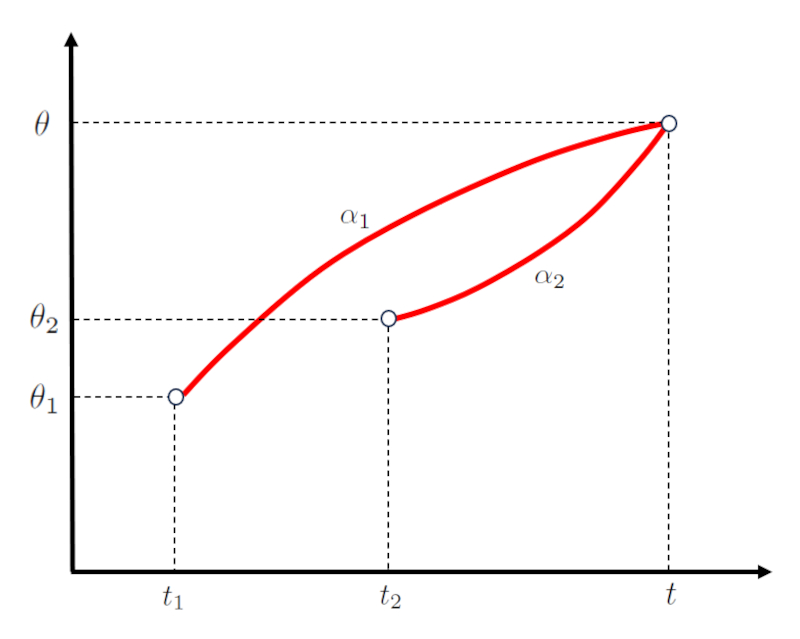
In einem Szenario mit der Bewegung von zwei Körpern stimmt der Winkel, in dem die Bahn des ersten endet, mit dem des zweiten Körpers überein bei die Kreuzungswinkel ($\theta$).
Ebenso stimmt die Zeit, zu der die Bahn des ersten endet, mit der des zweiten Körpers überein bei der Kreuzungszeit ($t$).
Für den ersten Körper hängt die Kreuzungswinkel ($\theta$) von der Anfangswinkel des ersten Körpers ($\theta_1$), die Anfangswinkelgeschwindigkeit des ersten Körpers ($\omega_{01}$), die Winkelbeschleunigung des ersten Körpers ($\alpha_1$), der Anfangszeit des ersten Objekts ($t_1$) ab, wie folgt:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
Während für den zweiten Körper hängt die Kreuzungswinkel ($\theta$) von der Anfangswinkel des zweiten Körpers ($\theta_2$), die Anfangswinkelgeschwindigkeit des zweiten Körpers ($\omega_{02}$), die Winkelbeschleunigung des zweiten Körpers ($\alpha_2$), der Anfangszeit des zweiten Objekts ($t_2$) ab, wie folgt:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Dies wird wie folgt dargestellt:
ID:(12514, 0)
Schnittpunkt bei konstanter Winkelbeschleunigung
Beschreibung 
Die Objekte können sich kreuzen, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen anfänglichen Winkeln und Winkelgeschwindigkeiten mit Winkelbeschleunigungen bewegen, die es ihnen ermöglichen, am Ende der Reise im Winkel und zur gleichen Zeit übereinzustimmen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
| $ \Delta\omega = \omega_2 - \omega_1 $ |
und der verstrichenen Zeit
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
innerhalb dieses Zeitintervalls.
(ID 3234)
Die Definition der durchschnittlichen Winkelbeschleunigung basiert auf dem zur ckgelegten Winkel
| $ \Delta\omega = \omega_2 - \omega_1 $ |
und der verstrichenen Zeit
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die durchschnittliche Winkelbeschleunigung definiert
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
innerhalb dieses Zeitintervalls.
(ID 3234)
Angesichts dessen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) gem
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) laut
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ist, folgt daraus, dass
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Unter der Annahme, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Constant Angular Acceleration ($\alpha_0$) ist
| $ \bar{\alpha} = \alpha_0 $ |
und angenommen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die konstante Beschleunigung ($a_0$) ist
| $ a_0 = \bar{a} $ |
ergibt sich folgende Gleichung:
| $ a = r \alpha $ |
(ID 3236)
Angesichts dessen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) gem
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$) laut
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
ist, folgt daraus, dass
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Unter der Annahme, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) gleich die Constant Angular Acceleration ($\alpha_0$) ist
| $ \bar{\alpha} = \alpha_0 $ |
und angenommen, dass die Mittlere Beschleunigung ($\bar{a}$) gleich die konstante Beschleunigung ($a_0$) ist
| $ a_0 = \bar{a} $ |
ergibt sich folgende Gleichung:
| $ a = r \alpha $ |
(ID 3236)
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) konstant und gleich die Constant Angular Acceleration ($\alpha_0$) ist, dann gilt die folgende Gleichung:
| $ \bar{\alpha} = \alpha_0 $ |
Daher, unter Ber cksichtigung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) zusammen mit die Winkelgeschwindigkeit ($\omega$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
und der Abgelaufene Zeit ($\Delta t$) in Bezug auf der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
kann die Gleichung f r die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
wie folgt ausgedr ckt werden:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Durch Aufl sen erhalten wir:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung ($\bar{\alpha}$) konstant und gleich die Constant Angular Acceleration ($\alpha_0$) ist, dann gilt die folgende Gleichung:
| $ \bar{\alpha} = \alpha_0 $ |
Daher, unter Ber cksichtigung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) zusammen mit die Winkelgeschwindigkeit ($\omega$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
und der Abgelaufene Zeit ($\Delta t$) in Bezug auf der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
kann die Gleichung f r die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
wie folgt ausgedr ckt werden:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Durch Aufl sen erhalten wir:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
Im Fall von die Constant Angular Acceleration ($\alpha_0$) folgt die Winkelgeschwindigkeit ($\omega$) als Funktion von der Zeit ($t$) einer linearen Beziehung mit der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) in der Form:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Da der zur ckgelegte Winkel gleich der Fl che unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
$\omega_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
hinzugef gt werden.
Dies f hrt uns zu dem Ausdruck f r der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Im Fall von die Constant Angular Acceleration ($\alpha_0$) folgt die Winkelgeschwindigkeit ($\omega$) als Funktion von der Zeit ($t$) einer linearen Beziehung mit der Startzeit ($t_0$) und die Anfängliche Winkelgeschwindigkeit ($\omega_0$) in der Form:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Da der zur ckgelegte Winkel gleich der Fl che unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
$\omega_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
hinzugef gt werden.
Dies f hrt uns zu dem Ausdruck f r der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit ($\omega$) aufl sen, die die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Constant Angular Acceleration ($\alpha_0$) umfasst:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
erhalten wir den folgenden Ausdruck f r die Zeit:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Diese L sung kann in die Gleichung eingesetzt werden, um der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt zu berechnen:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
was in der folgenden Gleichung resultiert:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit ($\omega$) aufl sen, die die Variablen die Anfängliche Winkelgeschwindigkeit ($\omega_0$), der Zeit ($t$), der Startzeit ($t_0$) und die Constant Angular Acceleration ($\alpha_0$) umfasst:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
erhalten wir den folgenden Ausdruck f r die Zeit:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
Diese L sung kann in die Gleichung eingesetzt werden, um der Winkel ($\theta$) unter Verwendung von der Anfangswinkel ($\theta_0$) wie folgt zu berechnen:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
was in der folgenden Gleichung resultiert:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
(ID 4386)
Beispiele
(ID 15416)
In einem Szenario mit der Bewegung von zwei K rpern ndert der erste die Winkelgeschwindigkeitsunterschied des ersten Körpers ($\Delta\omega_1$) w hrend die Reisezeit des ersten Objekts ($\Delta t_1$) mit die Winkelbeschleunigung des ersten Körpers ($\alpha_1$).
| $ \alpha_1 \equiv \displaystyle\frac{ \Delta\omega_1 }{ \Delta t_1 }$ |
Anschlie end bewegt sich der zweite K rper vorw rts und ndert die Winkelgeschwindigkeitsdifferenz des zweiten Körpers ($\Delta\omega_2$) w hrend die Reisezeit des zweiten Objekts ($\Delta t_2$) mit die Winkelbeschleunigung des zweiten Körpers ($\alpha_2$).
| $ \alpha_2 \equiv \displaystyle\frac{ \Delta\omega_2 }{ \Delta t_2 }$ |
Grafisch dargestellt erhalten wir ein Geschwindigkeits-Zeit-Diagramm wie unten gezeigt:
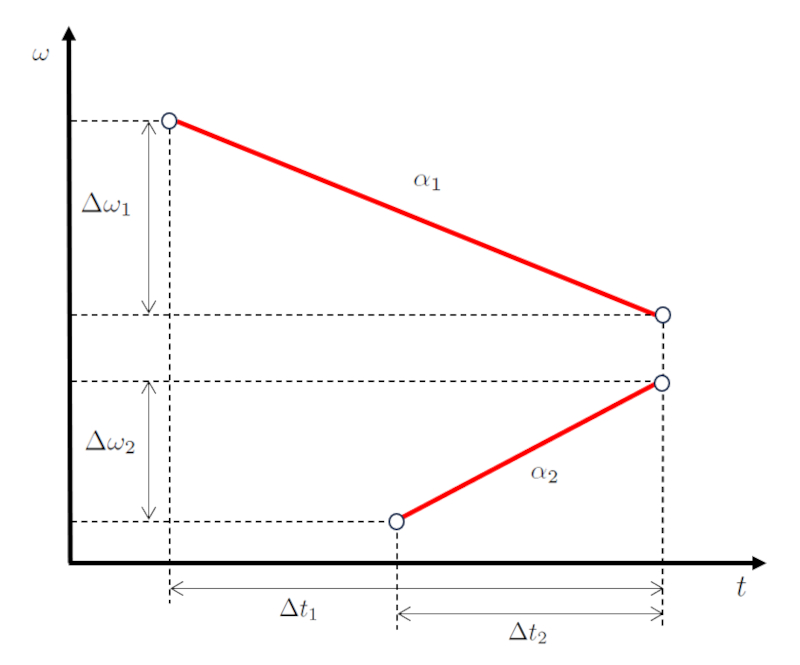
Der Schl ssel hierbei ist, dass die Werte die Winkelgeschwindigkeitsunterschied des ersten Körpers ($\Delta\omega_1$) und die Winkelgeschwindigkeitsdifferenz des zweiten Körpers ($\Delta\omega_2$), und die Werte die Reisezeit des ersten Objekts ($\Delta t_1$) und die Reisezeit des zweiten Objekts ($\Delta t_2$), so gew hlt sind, dass beide K rper im Winkel und zur gleichen Zeit zusammenfallen.
(ID 10579)
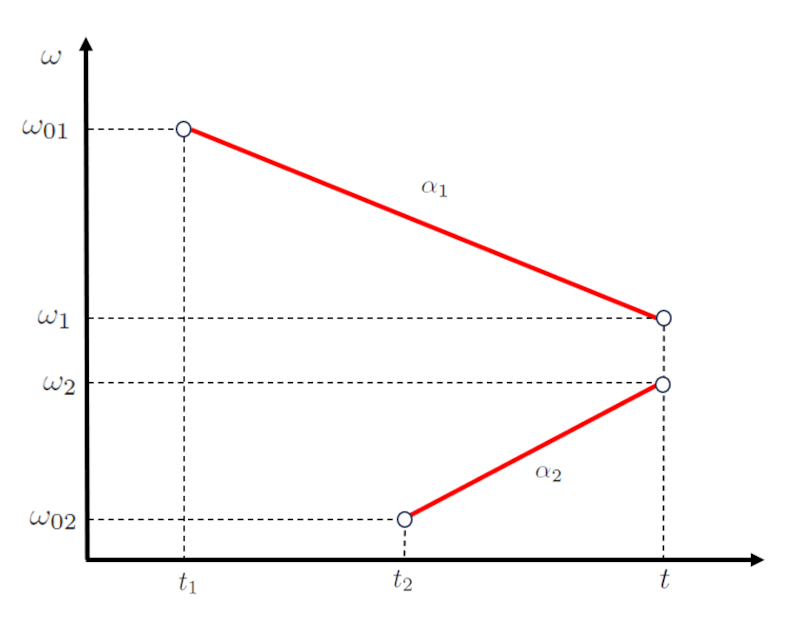
In einem Szenario mit zwei K rpern kann die Bewegung des ersten durch eine Funktion beschrieben werden, die die Punkte die Anfangswinkelgeschwindigkeit des ersten Körpers ($\omega_{01}$), die Endwinkelgeschwindigkeit des ersten Körpers ($\omega_1$), der Kreuzungszeit ($t$) und der Anfangszeit des ersten Objekts ($t_1$) involviert, dargestellt durch eine Gerade mit einer Steigung von die Winkelbeschleunigung des ersten Körpers ($\alpha_1$):
| $ \omega_1 = \omega_{01} + \alpha_1 ( t - t_1 )$ |
F r die Bewegung des zweiten K rpers, definiert durch die Punkte die Anfangswinkelgeschwindigkeit des zweiten Körpers ($\omega_{02}$), die Endgültige Winkelgeschwindigkeit des zweiten Körpers ($\omega_2$), der Anfangszeit des zweiten Objekts ($t_2$) und der Kreuzungszeit ($t$), wird eine zweite Gerade mit einer Steigung von die Winkelbeschleunigung des zweiten Körpers ($\alpha_2$) verwendet:
| $ \omega_2 = \omega_{02} + \alpha_2 ( t - t_2 )$ |
Dies wird wie folgt dargestellt:
(ID 9872)
In einem Szenario mit der Bewegung von zwei K rpern stimmt der Winkel, in dem die Bahn des ersten endet, mit dem des zweiten K rpers berein bei die Kreuzungswinkel ($\theta$).
Ebenso stimmt die Zeit, zu der die Bahn des ersten endet, mit der des zweiten K rpers berein bei der Kreuzungszeit ($t$).
F r den ersten K rper h ngt die Kreuzungswinkel ($\theta$) von der Anfangswinkel des ersten Körpers ($\theta_1$), die Anfangswinkelgeschwindigkeit des ersten Körpers ($\omega_{01}$), die Winkelbeschleunigung des ersten Körpers ($\alpha_1$), der Anfangszeit des ersten Objekts ($t_1$) ab, wie folgt:
| $ \theta = \theta_1 + \omega_{01} ( t - t_1 )+\displaystyle\frac{1}{2} \alpha_1 ( t - t_1 )^2$ |
W hrend f r den zweiten K rper h ngt die Kreuzungswinkel ($\theta$) von der Anfangswinkel des zweiten Körpers ($\theta_2$), die Anfangswinkelgeschwindigkeit des zweiten Körpers ($\omega_{02}$), die Winkelbeschleunigung des zweiten Körpers ($\alpha_2$), der Anfangszeit des zweiten Objekts ($t_2$) ab, wie folgt:
| $ \theta = \theta_2 + \omega_{02} ( t - t_2 )+\displaystyle\frac{1}{2} \alpha_2 ( t - t_2 )^2$ |
Dies wird wie folgt dargestellt:

(ID 12514)
(ID 15427)
ID:(1451, 0)
