Utilizador: 
Fluxo laminar, tinta
Descrição 
Uma forma eficaz de mostrar o fluxo laminar é injetar tinta em um fluxo usando uma agulha fina que não o perturbe. Essa técnica permite a visualização clara das camadas de fluido deslizando sem se misturar entre si. A tinta se dispersa no fluido de maneira ordenada, criando linhas distintas que revelam a direção e o padrão do fluxo laminar. Esse método é amplamente utilizado em experimentos e demonstrações para ilustrar visualmente as características e propriedades do fluxo laminar de maneira impactante.
ID:(7059, 0)
Imagens de fluxo laminar
Descrição
A observação em laboratório mostra como a tinta desenha uma linha (neste caso, vermelha). Se o experimento for repetido em diferentes posições, é observado um padrão de camadas, indicando que o fluxo é laminar.
Líquidos que fluem de forma laminar apresentam um canal suave, sem a formação de redemoinhos ou movimentos laterais bruscos.
ID:(7060, 0)
Fluxo turbulento, tinta
Descrição
Uma maneira de visualizar o fluxo turbulento é injetar tinta em um fluxo usando uma agulha fina que não perturbe o mesmo.
O comportamento resultante apresenta uma desvio abrupto e um grau de difusão causados pelas turbulências no fluxo.
ID:(7064, 0)
Imagem de fluxo turbulento
Descrição
No laboratório, é injetada tinta azul que se desvia significativamente de um fluxo linear, revelando assim a presença de vórtices e um grau de difusão devido a perturbações de menor amplitude.
ID:(7067, 0)
Evolução da turbulência de acordo com o número de Reynold
Conceito
O comportamento do fluxo ao redor de uma esfera sofre mudanças dramáticas dependendo de o número de Reynolds ($Re$), que é calculado em função de la dimensão típica do sistema ($R$), que neste caso corresponde ao raio da esfera. Além disso, o número de Reynolds ($Re$) é uma função de la velocidade média do fluido ($v$), la densidade ($\rho$) e la viscosidade ($\eta$), conforme:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
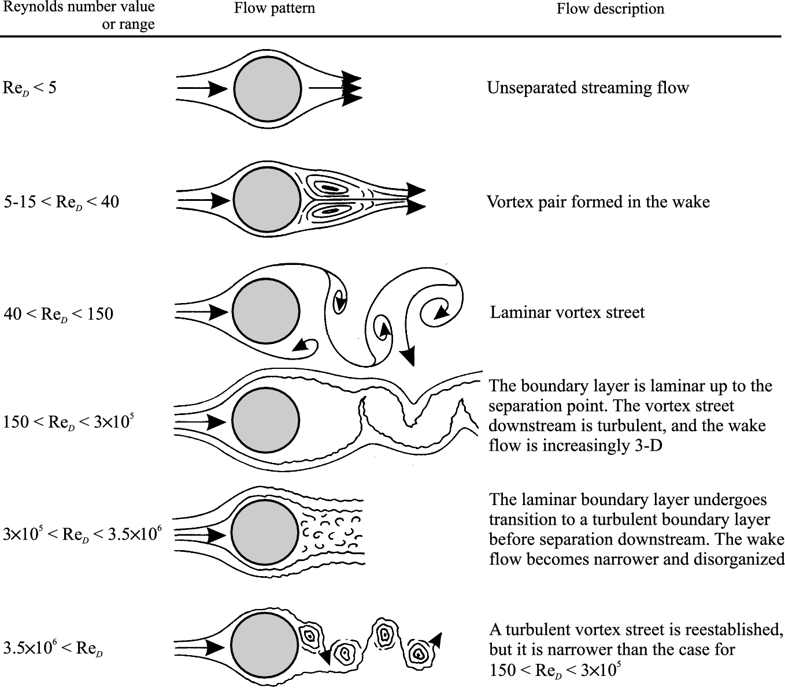
o número de Reynolds ($Re$) expressa a proporção entre a inércia e a viscosidade do sistema. Quando a viscosidade domina, o fluxo tem um comportamento laminar, enquanto que, no caso oposto, a inércia prevalece. No primeiro caso, o meio tem tempo para se adaptar, enquanto no segundo, não há tempo suficiente, resultando na formação de vórtices ou até mesmo em um comportamento caótico.
O diagrama a seguir resume os diferentes comportamentos do fluxo:
ID:(1890, 0)
Coeficiente de resistência hidráulica
Conceito
O coeficiente de resistência ($C_W$) varia em função de o número de Reynolds ($Re$) da seguinte maneira:
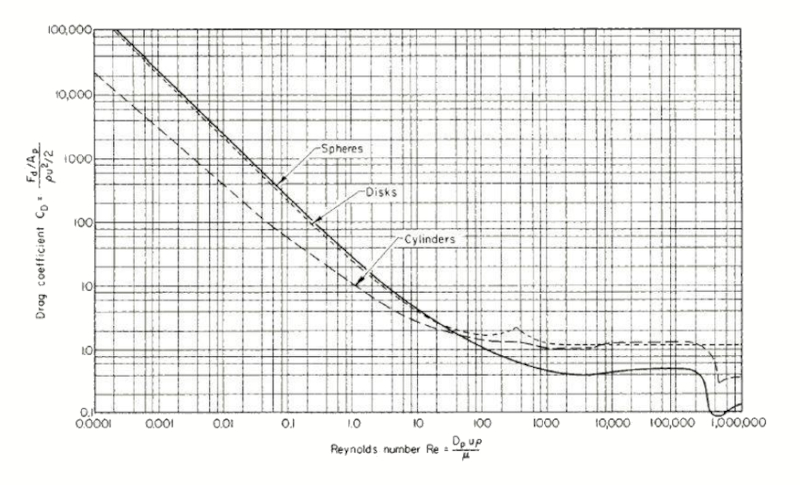
que pode ser estimada pela equação empírica:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Assim, la força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) por meio de:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Simulação de escoamento em torno de um obstáculo
Descrição
Para estudar o escoamento na fronteira entre os regimes laminar e turbulento, você pode utilizar o simulador desenvolvido por Dan Schroeder, do Departamento de Física da Weber State University:
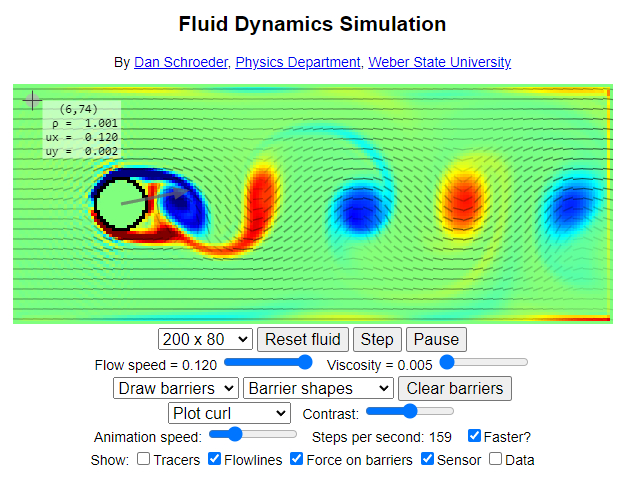
Acesse o simulador diretamente através do seguinte link: Simulação de Dinâmica de Fluidos.
ID:(15901, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15733, 0)
Número de Reynolds
Equação
O critério chave para determinar se um meio é laminar ou turbulento é o chamado número de Reynolds, que compara a energia associada à inércia com aquela associada à viscosidade. A primeira depende de la densidade ($\rho$), la velocidade média do fluido ($v$) e la dimensão típica do sistema ($R$), enquanto a segunda depende de la viscosidade ($\eta$), definindo-o como:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Sustentação
Equação
Para gerar uma pressão maior abaixo do que acima da asa e gerar sustentação, utiliza-se o princípio de Bernoulli, corrigindo a falta de conservação da densidade de energia com um coeficiente de elevação ($C_L$). A pressão sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) através da seguinte fórmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
e para o coeficiente de elevação ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Força de resistência
Equação
La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte fórmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De maneira semelhante à forma como a equação para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) será equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no cálculo de la força de resistência ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
O coeficiente de arrasto é medido e, em fluxos turbulentos sobre corpos aerodinâmicos, geralmente se obtêm valores em torno de 0.4.
ID:(4418, 0)
Coeficiente de arrasto de uma esfera
Equação
Empiricamente, o coeficiente de resistência ($C_W$) pode ser modelado em função de o número de Reynolds ($Re$) da seguinte maneira:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)