Usuario:
Flujo laminar, tinta
Descripción 
Una forma efectiva de visualizar el flujo laminar es mediante la inyección de tinta en un flujo utilizando una aguja delgada que no perturbe dicho flujo. Esta técnica permite observar claramente las capas de fluido deslizándose sin mezclarse entre sí. La tinta se dispersa en el fluido de manera ordenada, creando líneas definidas que revelan la dirección y el patrón del flujo laminar. Esta metodología es ampliamente utilizada en experimentos y demostraciones para ilustrar las características y propiedades del flujo laminar de forma visualmente impactante.
ID:(7059, 0)
Imágenes de flujo laminar
Descripción
La observación en el laboratorio muestra cómo la tinta dibuja una línea (en este caso roja). Si se repite el experimento en distintas posiciones, se observa un patrón de capas, lo que indica que el flujo es laminar.
Los líquidos que fluyen de forma laminar exhiben un flujo suave, sin la formación de vórtices ni movimientos laterales bruscos.
ID:(7060, 0)
Flujo turbulento, tinta
Descripción
Una forma de visualizar un flujo turbulento es inyectar tinta en un flujo mediante una aguja delgada que no perturbe dicho flujo.
El comportamiento resultante muestra una desviación abrupta y un grado de difusión causados por las turbulencias en el flujo.
ID:(7064, 0)
Imagen de flujo turbulento
Descripción
En el laboratorio, se inyecta tinta azul que se desvía radicalmente de un flujo lineal, mostrando así la presencia de torbellinos y un grado de difusión debido a perturbaciones de menor amplitud.
ID:(7067, 0)
Evolución de turbulencias según número Reynold
Concepto
El comportamiento del flujo alrededor de una esfera experimenta cambios dramáticos según el número de Reynold ($Re$), calculado en función de la dimensión típica del sistema ($R$), que en este caso corresponde al radio de la esfera. Además, el número de Reynold ($Re$) es una función de la velocidad media del fluido ($v$), la densidad ($\rho$) y la viscosidad ($\eta$) según:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
el número de Reynold ($Re$) expresa la proporción entre la inercia y la viscosidad del sistema. Mientras la viscosidad domina, el flujo se comporta de manera laminar, pero en el caso contrario, domina la inercia. En el primer caso, el medio tiene tiempo de adaptarse, mientras que en el segundo, el flujo no dispone del tiempo suficiente, generando zonas de vórtices o incluso comportamientos caóticos.
El siguiente diagrama resume los diferentes comportamientos:
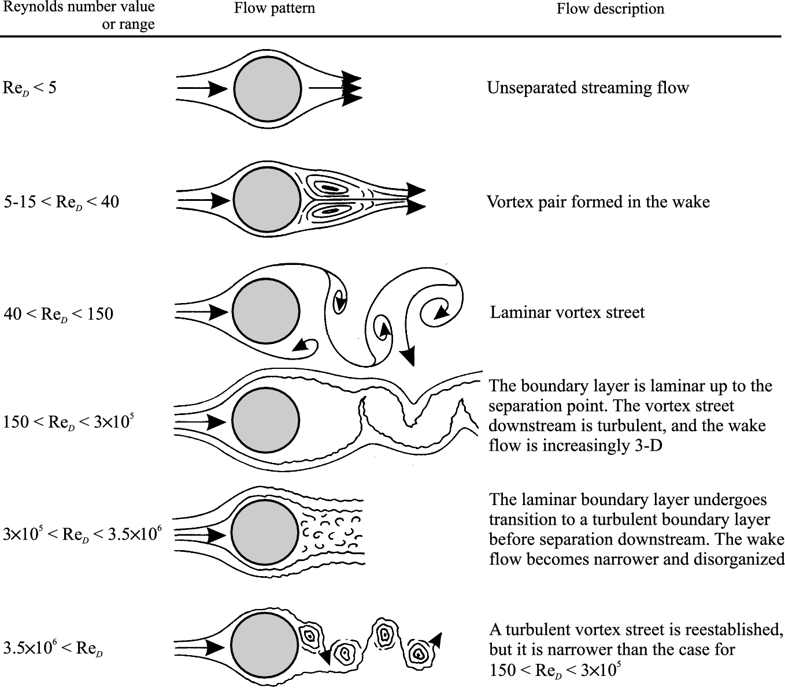
Esquema del tipo de flujo según numero de Reynold (libro Introduction to Transport Phenomena Modeling, Gianpaolo Ruocco - https://link.springer.com/chapter/10.1007/978-3-319-66822-2_3)
ID:(1890, 0)
Coeficiente de resistencia hidraulica
Concepto
El coeficiente de resistencia ($C_W$) varía en función de el número de Reynold ($Re$) según:
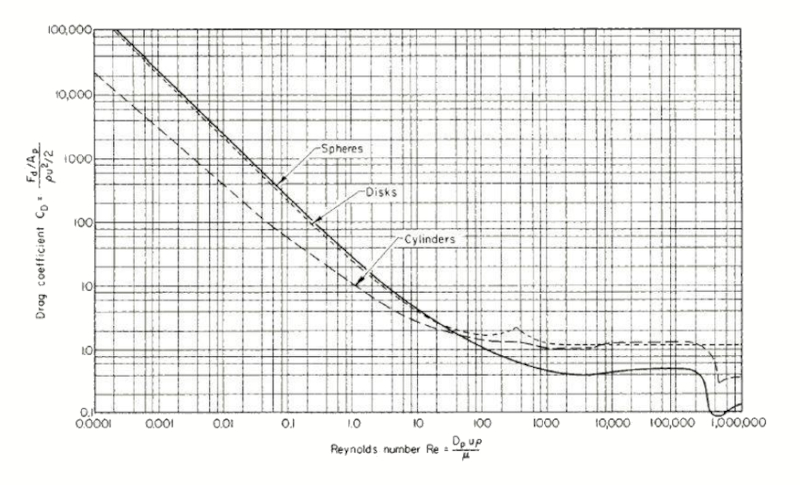
que se puede estimar con la ecuación empírica:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
De este modo, la fuerza de resistencia ($F_W$) se puede calcular con la densidad ($\rho$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) mediante:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Simulación flujo en torno a obstaculo
Descripción
Para analizar un flujo en el límite entre el régimen laminar y turbulento, se puede utilizar el simulador desarrollado por Dan Schroeder, del Departamento de Física de la Universidad Weber State:
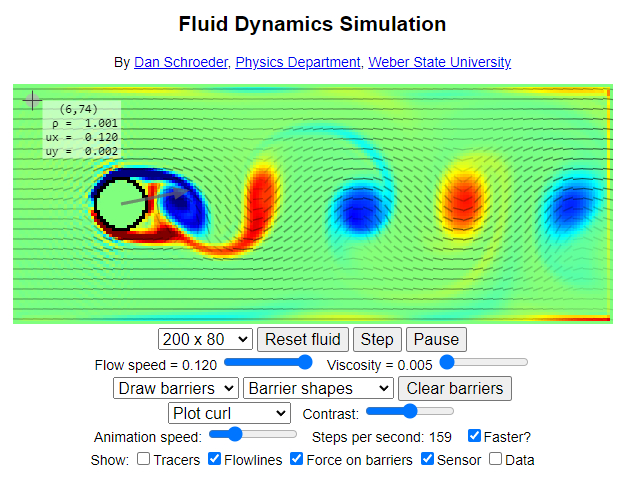
Accede al simulador directamente a través del siguiente enlace: Simulación de Dinámica de Fluidos.
ID:(15901, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15733, 0)
Número de Reynold
Ecuación
El criterio clave para determinar si un medio es laminar o turbulento es el llamado numero de Reynold que compara la energía asociada a la inercia con aquella asociada a la viscosiadad. La primera depende de la densidad ($\rho$), la velocidad media del fluido ($v$) y la dimensión típica del sistema ($R$) mientras que la segunda de la viscosidad ($\eta$) con lo que se define:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Fuerza de sustentación
Ecuación
Para crear una presión mayor debajo que encima del ala y generar sustentación, se emplea la Ley de Bernoulli, corrigiendo la falta de conservación de la densidad de energía mediante un coeficiente de sustentación ($C_L$). La presión sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente fórmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
y para el coeficiente de sustentación ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtenemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Fuerza de resistencia
Ecuación
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente fórmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De forma similar a cómo se derivó la ecuación para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
en esta analogía, lo que corresponde a la superficie que genera sustentación ($S_w$) será equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodinámicos, generalmente se registran valores alrededor de 0.4.
ID:(4418, 0)
Coeficiente de arrastre de una esfera
Ecuación
Empíricamente, el coeficiente de resistencia ($C_W$) se puede modelar en función de el número de Reynold ($Re$) de la siguiente manera:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)