Benützer:
Laminar Flow, Tinte
Beschreibung 
Eine effektive Methode, um laminare Strömung zu zeigen, besteht darin, Tinte in einen Fluss einzuspritzen, indem eine dünne Nadel verwendet wird, die diesen nicht stört. Diese Technik ermöglicht eine klare Visualisierung der Flüssigkeitsschichten, die sich ohne Vermischung gegeneinander bewegen. Die Tinte verteilt sich geordnet im Fluid und erzeugt deutlich erkennbare Linien, die die Richtung und das Muster der laminaren Strömung offenbaren. Diese Methode wird häufig in Experimenten und Demonstrationen eingesetzt, um die Merkmale und Eigenschaften der laminaren Strömung auf visuell beeindruckende Weise zu veranschaulichen.
ID:(7059, 0)
Laminare Strömungsbilder
Beschreibung
Die Beobachtung im Labor zeigt, wie Tinte eine Linie zieht (in diesem Fall rot). Wenn das Experiment an verschiedenen Positionen wiederholt wird, zeigt sich ein Schichtmuster, was auf laminare Strömung hinweist.
Flüssigkeiten, die laminar fließen, zeigen einen sanften Kanal, ohne Wirbelbildung oder abrupte seitliche Bewegungen.
ID:(7060, 0)
Turbulente Strömung, Tinte
Beschreibung
Eine Möglichkeit, turbulente Strömung darzustellen, besteht darin, Tinte mit einer dünnen Nadel in einen Fluss zu injizieren, ohne diesen zu stören.
Das resultierende Verhalten zeigt eine abrupte Abweichung und eine gewisse Diffusion, die durch die Turbulenzen in der Strömung verursacht werden.
ID:(7064, 0)
Turbulentes Strömungsbild
Beschreibung
Im Labor wird blaue Tinte injiziert, die sich signifikant von einem linearen Fluss abweicht und damit das Vorhandensein von Wirbeln und eine gewisse Diffusion aufgrund geringerer Störungen zeigt.
ID:(7067, 0)
Turbulenzentwicklung nach Reynold-Zahl
Konzept
Das Verhalten des Flusses um eine Kugel ändert sich dramatisch in Abhängigkeit von der Anzahl der Reynold ($Re$), das als Funktion von die Typische Abmessungen des Systems ($R$) berechnet wird, wobei die Typische Abmessungen des Systems ($R$) in diesem Fall dem Radius der Kugel entspricht. Zudem ist der Anzahl der Reynold ($Re$) eine Funktion von die Mittlere Geschwindigkeit der Flüssigkeit ($v$), die Dichte ($\rho$) und die Viskosität ($\eta$), gemäß:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
der Anzahl der Reynold ($Re$) beschreibt das Verhältnis zwischen Trägheit und Viskosität des Systems. Solange die Viskosität dominiert, zeigt der Fluss ein laminares Verhalten, während im umgekehrten Fall die Trägheit dominiert. Im ersten Fall hat das Medium genug Zeit, sich anzupassen, während im zweiten Fall nicht genügend Zeit zur Verfügung steht, was zur Bildung von Wirbeln oder sogar zu chaotischem Verhalten führt.
Das folgende Diagramm fasst die verschiedenen Fließverhalten zusammen:
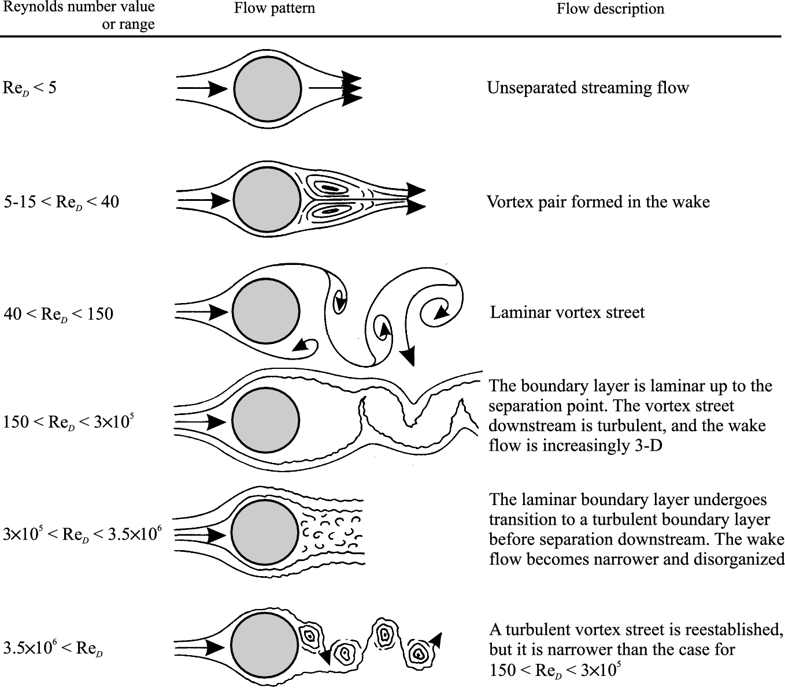
Fließschema nach Reynold-Nummer (Buch Introduction to Transport Phenomena Modeling, Gianpaolo Ruocco - https://link.springer.com/chapter/10.1007/978-3-319-66822-2_3)
ID:(1890, 0)
Hydraulischer Widerstandskoeffizient
Konzept
Der Widerstandskoeffizient ($C_W$) variiert in Abhängigkeit von der Anzahl der Reynold ($Re$) wie folgt:
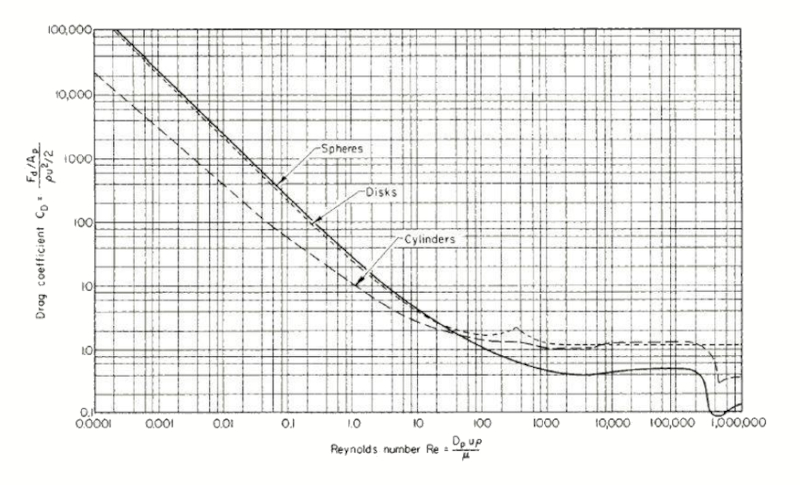
was mit der empirischen Gleichung geschätzt werden kann:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Auf diese Weise kann die Widerstandskraft ($F_W$) mithilfe von die Dichte ($\rho$), der Gesamtobjektprofil ($S_p$) und die Geschwindigkeit in Bezug auf das Medium ($v$) berechnet werden:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Simulation der Umströmung eines Hindernisses
Beschreibung
Um den Fluss an der Grenze zwischen laminarer und turbulenter Strömung zu untersuchen, kann der Simulator von Dan Schroeder vom Physikdepartment der Weber State University verwendet werden:
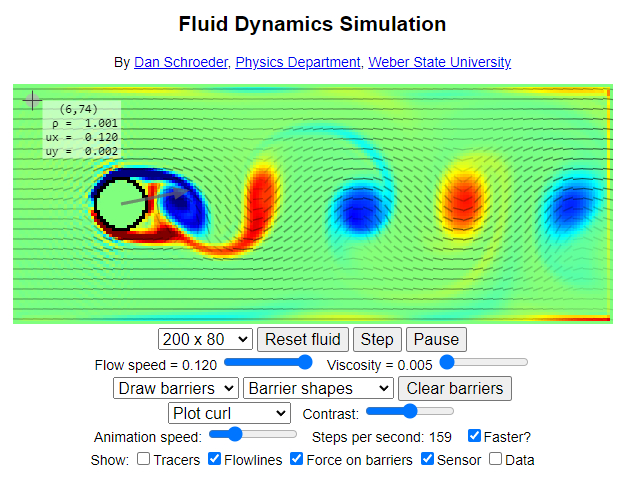
Der direkte Zugriff auf den Simulator erfolgt über den folgenden Link: Fluid Dynamics Simulation.
ID:(15901, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15733, 0)
Reynold Zahl
Gleichung
Das entscheidende Kriterium zur Bestimmung, ob ein Medium laminar oder turbulent ist, ist die sogenannte Reynolds-Zahl, die die Energie, die mit der Trägheit verbunden ist, mit derjenigen vergleicht, die mit der Viskosität verbunden ist. Erstere hängt von die Dichte ($\rho$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Typische Abmessungen des Systems ($R$) ab, während letztere von die Viskosität ($\eta$) abhängt. Sie wird definiert als:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Auftriebskraft
Gleichung
Um einen höheren Druck unterhalb als oberhalb des Flügels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck über dem Flügel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel geschätzt werden:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
und für der Koeffizient Fahrstuhl ($C_L$), definiert als
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
erhalten wir
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Widerstandskraft
Gleichung
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente fórmula:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Ähnlich wie die Gleichung für die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Der Widerstandsbeiwert wird gemessen und bei turbulenten Strömungen über aerodynamischen Körpern werden üblicherweise Werte um 0,4 ermittelt.
ID:(4418, 0)
Widerstandsbeiwert einer Kugel
Gleichung
Empirisch kann der Widerstandskoeffizient ($C_W$) in Abhängigkeit von der Anzahl der Reynold ($Re$) wie folgt modelliert werden:
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)