Utilisateur:
Flux laminaire, encre
Description 
Une manière efficace de montrer l'écoulement laminaire est d'injecter de l'encre dans un flux à l'aide d'une aiguille fine qui ne le perturbe pas. Cette technique permet de visualiser clairement les couches de fluide glissant les unes sur les autres sans se mélanger. L'encre se dispersera dans le fluide de manière ordonnée, créant des lignes distinctes qui révèlent la direction et le motif de l'écoulement laminaire. Cette méthode est largement utilisée dans les expériences et les démonstrations pour illustrer de manière visuellement impactante les caractéristiques et les propriétés de l'écoulement laminaire.
ID:(7059, 0)
Images de flux laminaire
Description
L'observation en laboratoire montre comment l'encre dessine une ligne (dans ce cas, rouge). Si l'expérience est répétée à différentes positions, on observe un schéma de couches, ce qui indique un écoulement laminaire.
Les liquides s'écoulant de manière laminaire présentent un écoulement régulier, sans tourbillons ni mouvements latéraux brusques.
ID:(7060, 0)
Écoulement turbulent, encre
Description
Une façon de visualiser un écoulement turbulent est d'injecter de l'encre dans un écoulement à l'aide d'une fine aiguille qui ne perturbe pas celui-ci.
Le comportement obtenu montre une déviation abrupte et un degré de diffusion causés par les turbulences dans l'écoulement.
ID:(7064, 0)
Image d'écoulement turbulent
Description
En laboratoire, de l'encre bleue est injectée, ce qui s'écarte considérablement d'un écoulement linéaire, révélant ainsi la présence de tourbillons et un degré de diffusion dû à des perturbations de plus faible amplitude.
ID:(7067, 0)
Evolution de la turbulence selon le nombre de Reynold
Concept
Le comportement de lécoulement autour dune sphère change de manière drastique en fonction de le le numéro de Reynold ($Re$), calculé en fonction de a dimension typique du système ($R$), qui dans ce cas correspond au rayon de la sphère. De plus, le le numéro de Reynold ($Re$) est une fonction de a vitesse moyenne du fluide ($v$), a densité ($\rho$) et a viscosité ($\eta$), selon :
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
le le numéro de Reynold ($Re$) exprime le rapport entre l'inertie et la viscosité du système. Lorsque la viscosité domine, lécoulement présente un comportement laminaire, tandis que lorsque l'inertie prend le dessus, l'écoulement devient turbulent. Dans le premier cas, le milieu a le temps de s'adapter, tandis que dans le second, le flux ne dispose pas de suffisamment de temps, ce qui entraîne la formation de vortex ou même un comportement chaotique.
Le diagramme suivant résume les différents comportements de lécoulement :
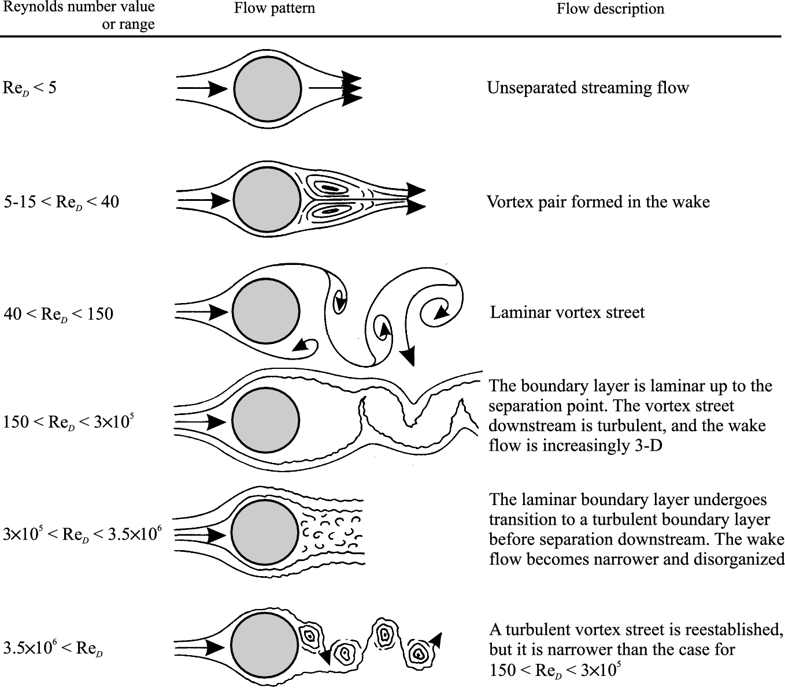
ID:(1890, 0)
Coefficient de résistance hydraulique
Concept
Le coefficient de résistance ($C_W$) varie en fonction de le le numéro de Reynold ($Re$) comme suit :
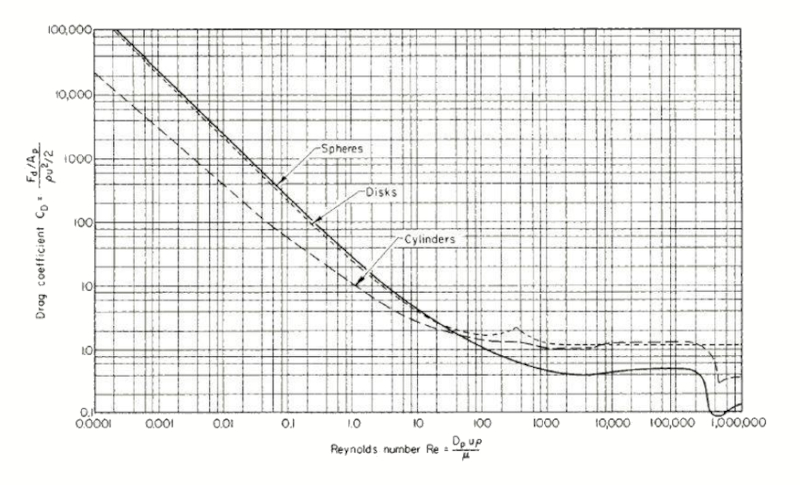
qui peut être estimé avec léquation empirique :
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
Ainsi, a force de résistance ($F_W$) peut être calculé avec a densité ($\rho$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) à laide de :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
ID:(7065, 0)
Simulation d'écoulement autour d'un obstacle
Description
Pour étudier l'écoulement à la limite entre les régimes laminaire et turbulent, vous pouvez utiliser le simulateur développé par Dan Schroeder, du Département de Physique de l'Université Weber State :
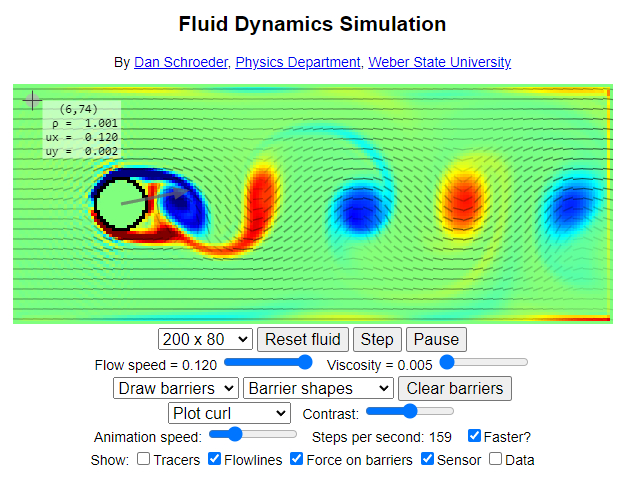
Accédez directement au simulateur via le lien suivant : Simulation de Dynamique des Fluides.
ID:(15901, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$
C_W =24*(1+ Re ^0.687)/ Re
$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$
F_W = rho * S_p * C_W * v ^2/2
$ Re =\displaystyle\frac{ \rho R v }{ \eta }$
Re = rho * R * v / eta
ID:(15733, 0)
Le numéro de Reynold
Équation
Le critère clé pour déterminer si un milieu est laminé ou turbulent est le numéro de Reynolds, qui compare l'énergie associée à l'inertie à celle associée à la viscosité. La première dépend de a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a dimension typique du système ($R$), tandis que la seconde dépend de a viscosité ($\eta$), le définissant ainsi :
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Soulevez
Équation
Pour générer une pression plus élevée en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilisé pour corriger le manque de conservation de la densité d'énergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut être estimée en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) grâce à la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous considérons a surface génératrice de portance ($S_w$), défini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), défini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Force de résistance
Équation
A force de résistance ($F_W$) peut être calculé en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
De manière similaire à la façon dont l'équation pour a force de levage ($F_L$) a été dérivée en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
dans cette analogie, ce qui correspond à A surface génératrice de portance ($S_w$) sera équivalent à Le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) à Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Le coefficient de traînée est mesuré et, dans les écoulements turbulents sur les corps aérodynamiques, les valeurs sont généralement autour de 0.4.
ID:(4418, 0)
Coefficient de traînée d'une sphère
Équation
Empiriquement, le coefficient de résistance ($C_W$) peut être modélisé en fonction de le le numéro de Reynold ($Re$) comme suit :
| $ C_W = \displaystyle\frac{24}{ Re }(1 + 0.15 Re ^{0.687})$ |
ID:(15900, 0)