Storyboard

No caso de um fluxo proveniente de vários canais e se dividindo em outros múltiplos canais iguais, a conservação do fluxo determina que a soma das taxas de fluxo dos canais iniciais deve ser igual à soma das taxas de fluxo dos canais finais. Este princípio deriva diretamente da equação de continuidade, que garante que o fluxo volumétrico total seja preservado. Os mesmos conceitos e equações aplicáveis a um único canal com seção variável, como a relação entre velocidade e área, continuam válidos neste cenário. Ao assumir que os canais são iguais, os cálculos são simplificados, permitindo uma distribuição uniforme do fluxo entre eles.

>Modelo

ID:(2097, 0)

Iframe

>Top

ID:(15913, 0)

Conceito

>Top

Durante um tempo decorrido ($\Delta t$), o fluido com uma velocidade média do fluido ($v$) se desloca um elemento de tubo ($\Delta s$). Se la seção ($S$) representa a quantidade de fluido que atravessa essa seção em o tempo decorrido ($\Delta t$), é calculada como:

$\Delta V = S \Delta s = Sv \Delta t$

Esta equação indica que o volume de fluido que flui através da seção la seção ($S$) durante um tempo decorrido ($\Delta t$) é igual ao produto da área da seção e a distância percorrida pelo fluido nesse tempo.

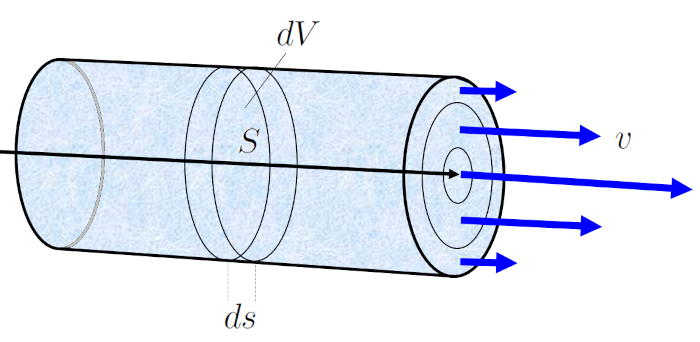
Isso facilita o cálculo de o elemento de volume ($\Delta V$), que é o volume de fluido que flui pelo canal em um período específico de o tempo decorrido ($\Delta t$), correspondente a o fluxo de volume ($J_V$).

ID:(2212, 0)

Conceito

>Top

O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:

e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):

Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:

Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:

É importante destacar que neste modelo:

A densidade de fluxo funciona como uma velocidade média em toda a seção do fluxo.

ID:(15715, 0)

Conceito

>Top

Considerando um tubo sem vazamentos ou adições de líquido, o fluxo de entrada através de o número de canais 1 ($N_1$), com uma taxa de fluxo de o fluxo de volume 1 ($J_{V1}$) por seção, será igual ao fluxo de saída através de o número de canais 2 ($N_2$), com uma taxa de fluxo de o fluxo de volume 2 ($J_{V2}$) por seção:

Dentro de um canal ou tubo, é comum ocorrer variações na área da seção transversal, seja por ampliação ou redução:

Essas variações impactam diretamente a velocidade do fluxo, representada por la densidade de fluxo ($j_s$). Se a área da seção transversal diminui, a velocidade aumenta, e se a área aumenta, a velocidade diminui, de acordo com la seção de tubo ($S$), para manter o fluxo de volume ($J_V$) constante, conforme indicado pela seguinte equação:

A conservação do fluxo, juntamente com a definição da densidade do fluxo, resulta na lei de conservação, onde o número de canais 1 ($N_1$), o número de canais 2 ($N_2$), la seção no ponto 1 ($S_1$), la seção no ponto 2 ($S_2$), la densidade de fluxo 1 ($j_{s1}$) e la densidade de fluxo 2 ($j_{s2}$) atendem à condição:

ID:(15915, 0)

Conceito

>Top

A equação de continuidade pressupõe que o fluxo seja uniforme, sem fluxos reversos ou turbulências presentes. Portanto, é necessário verificar se o fluxo é realmente laminar e livre de turbulências, especialmente ao aplicar a equação para analisar o fluxo de fluidos em tubos e canais.

Existem vários métodos para detectar turbulências no fluxo, como o uso de medidores de fluxo ou observação visual do fluxo. É essencial garantir que o fluxo seja estável antes de aplicar a equação de continuidade, pois qualquer perturbação no fluxo pode afetar a precisão dos cálculos e a eficiência geral do sistema.

ID:(978, 0)

Top

>Top

Parâmetros

$\pi$

pi

Pi

rad

Variáveis

$\Delta s_1$

Ds_1

Comprimento do elemento 1

m

$\Delta s_2$

Ds_2

Comprimento do elemento 2

m

$j_{s1}$

j_s1

Densidade de fluxo 1

m/s

$j_{s2}$

j_s2

Densidade de fluxo 2

m/s

$J_{V1}$

J_V1

Fluxo de volume 1

m^3/s

$J_{V2}$

J_V2

Fluxo de volume 2

m^3/s

$N_1$

N_1

Número de canais 1

-

$N_2$

N_2

Número de canais 2

-

$r_1$

r_1

Raio da seção 1

m

$r_2$

r_2

Raio da seção 2

m

$S_1$

S_1

Seção no ponto 1

m^2

$S_2$

S_2

Seção no ponto 2

m^2

$\Delta t$

Dt

Tempo decorrido

s

$\Delta V_1$

DV_1

Volume do elemento 1

m^3

$\Delta V_2$

DV_2

Volume do elemento 2

m^3

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15914, 0)

Equação

>Top, >Modelo

Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma distância de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), então é igual a:

$\Delta V_1 = S_1 \Delta s_1$

$\Delta V = S \Delta s$

Condições

Variáveis

$\Delta s$

$\Delta s_1$

Comprimento do elemento 1

$m$

10294

$\Delta V$

$\Delta V_1$

Volume do elemento 1

$m^3$

10292

$S$

$S_1$

Seção no ponto 1

$m^2$

5257

Relação

ID:(3469, 1)

Equação

>Top, >Modelo

Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma distância de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), então é igual a:

$\Delta V_2 = S_2 \Delta s_2$

$\Delta V = S \Delta s$

Condições

Variáveis

$\Delta s$

$\Delta s_2$

Comprimento do elemento 2

$m$

10295

$\Delta V$

$\Delta V_2$

Volume do elemento 2

$m^3$

10293

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

ID:(3469, 2)

Equação

>Top, >Modelo

O fluxo de volume ($J_V$) corresponde a o volume de fluxo ($\Delta V$) que flui através do canal em o tempo decorrido ($\Delta t$). Portanto, temos:

$J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

Condições

Variáveis

$\Delta V$

$\Delta V_1$

Volume do elemento 1

$m^3$

10292

$J_V$

$J_{V1}$

Fluxo de volume 1

$m^3/s$

8478

$\Delta t$

Tempo decorrido

$s$

5103

Relação

ID:(4347, 1)

Equação

>Top, >Modelo

O fluxo de volume ($J_V$) corresponde a o volume de fluxo ($\Delta V$) que flui através do canal em o tempo decorrido ($\Delta t$). Portanto, temos:

$J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

Condições

Variáveis

$\Delta V$

$\Delta V_2$

Volume do elemento 2

$m^3$

10293

$J_V$

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

$\Delta t$

Tempo decorrido

$s$

5103

Relação

ID:(4347, 2)

Equação

>Top, >Modelo

La densidade de fluxo ($j_s$) está relacionado com la distância percorrida em um tempo ($\Delta s$), que é a distância que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:

$j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Condições

Variáveis

$j_s$

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$\Delta s$

$\Delta s_1$

Comprimento do elemento 1

$m$

10294

$\Delta t$

Tempo decorrido

$s$

5103

Relação

ID:(4348, 1)

Equação

>Top, >Modelo

La densidade de fluxo ($j_s$) está relacionado com la distância percorrida em um tempo ($\Delta s$), que é a distância que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:

$j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Condições

Variáveis

$j_s$

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$\Delta s$

$\Delta s_2$

Comprimento do elemento 2

$m$

10295

$\Delta t$

Tempo decorrido

$s$

5103

Relação

ID:(4348, 2)

Equação

>Top, >Modelo

Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) através da seguinte fórmula:

$j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$

$j_s = \displaystyle\frac{ J_V }{ S }$

Condições

Variáveis

$j_s$

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$J_V$

$J_{V1}$

Fluxo de volume 1

$m^3/s$

8478

$S$

$S_1$

Seção no ponto 1

$m^2$

5257

Relação

Desenvolvimento

O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):

$\Delta V = S \Delta s$

Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:

$j_s = \displaystyle\frac{ J_V }{ S }$

ID:(4349, 1)

Equação

>Top, >Modelo

Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) através da seguinte fórmula:

$j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$

$j_s = \displaystyle\frac{ J_V }{ S }$

Condições

Variáveis

$j_s$

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$J_V$

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

Desenvolvimento

O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:

$J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):

$\Delta V = S \Delta s$

Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:

$j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$

Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:

$j_s = \displaystyle\frac{ J_V }{ S }$

ID:(4349, 2)

Equação

>Top, >Modelo

Se a densidade permanecer constante, o mesmo princípio se aplica ao volume. Nesses casos, quando tratamos o fluxo como um fluido incompressível, nos referimos a ele como um fluido incompressível. Em outras palavras, se um determinado volume entra por uma extremidade através de vários tubos, a mesma quantidade de volume deve sair pela outra extremidade, distribuída pelos tubos de saída. Isso pode ser expresso pela igualdade entre o número de canais 1 ($N_1$) multiplicado por o fluxona posição 1 ($J_1$) e o número de canais 2 ($N_2$) multiplicado por o fluxona posição 2 ($J_2$), resultando na seguinte equação:

$N_1 J_{V1} = N_2 J_{V2}$

Condições

Variáveis

$J_{V1}$

Fluxo de volume 1

$m^3/s$

8478

$J_{V2}$

Fluxo de volume 2

$m^3/s$

8479

$N_1$

Número de canais 1

$-$

10447

$N_2$

Número de canais 2

$-$

10448

Relação

ID:(15912, 0)

Equação

>Top, >Modelo

O princípio da continuidade estabelece que o fluxo na entrada, dado pelo produto de o número de canais 1 ($N_1$), la densidade de fluxo 1 ($j_{s1}$) e la seção no ponto 1 ($S_1$), deve ser igual ao fluxo na saída, representado pelo produto de o número de canais 2 ($N_2$), la densidade de fluxo 2 ($j_{s2}$) e la seção no ponto 2 ($S_2$). A partir disso, deduz-se que:

$N_1 S_1 j_{s1} = N_2 S_2 j_{s2}$

Condições

Variáveis

$j_{s1}$

Densidade de fluxo 1

$m/s$

10288

$j_{s2}$

Densidade de fluxo 2

$m/s$

10289

$N_1$

Número de canais 1

$-$

10447

$N_2$

Número de canais 2

$-$

10448

$S_1$

Seção no ponto 1

$m^2$

5257

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

ID:(15911, 0)

Equação

>Top, >Modelo

La superfície de um disco ($S$) de um raio do disco ($r$) é calculada da seguinte forma:

$S_1 = \pi r_1 ^2$

$S = \pi r ^2$

Condições

Variáveis

$\pi$

Pi

3.1415927

$rad$

5057

$r$

$r_1$

Raio da seção 1

$m$

10286

$S$

$S_1$

Seção no ponto 1

$m^2$

5257

Relação

ID:(3804, 1)

Equação

>Top, >Modelo

La superfície de um disco ($S$) de um raio do disco ($r$) é calculada da seguinte forma:

$S_2 = \pi r_2 ^2$

$S = \pi r ^2$

Condições

Variáveis

$\pi$

Pi

3.1415927

$rad$

5057

$r$

$r_2$

Raio da seção 2

$m$

10287

$S$

$S_2$

Seção no ponto 2

$m^2$

5413

Relação

ID:(3804, 2)