Benützer:
Strömung einer Flüssigkeit mit mehreren Kanälen
Storyboard 
Im Fall eines Flusses, der aus mehreren Kanälen stammt und sich in andere gleich große Kanäle aufteilt, besagt das Prinzip der Flusserhaltung, dass die Summe der Durchflussraten der Eingangskanäle gleich der Summe der Durchflussraten der Ausgangskanäle sein muss. Dieses Prinzip leitet sich direkt aus der Kontinuitätsgleichung ab, die sicherstellt, dass der gesamte volumetrische Fluss erhalten bleibt. Die gleichen Konzepte und Gleichungen, die auf einen einzelnen Kanal mit variabler Querschnittsfläche angewendet werden, wie die Beziehung zwischen Geschwindigkeit und Fläche, bleiben in diesem Fall gültig. Durch die Annahme, dass die Kanäle gleich groß sind, wird die Berechnung vereinfacht, da der Fluss gleichmäßig auf die Kanäle verteilt wird.
ID:(2097, 0)
Volumenstrom
Konzept
Während ein Abgelaufene Zeit ($\Delta t$) bewegt sich die Flüssigkeit mit eine Mittlere Geschwindigkeit der Flüssigkeit ($v$) um ein Rohrelement ($\Delta s$). Wenn die Abschnitt ($S$) die Menge an Flüssigkeit darstellt, die in der Abgelaufene Zeit ($\Delta t$) diesen Abschnitt durchquert, wird sie wie folgt berechnet:
$\Delta V = S \Delta s = Sv \Delta t$
Diese Gleichung besagt, dass das Volumen der Flüssigkeit, das während ein Abgelaufene Zeit ($\Delta t$) durch den Abschnitt die Abschnitt ($S$) fließt, gleich dem Produkt aus der Querschnittsfläche und der zurückgelegten Distanz der Flüssigkeit in dieser Zeit ist.
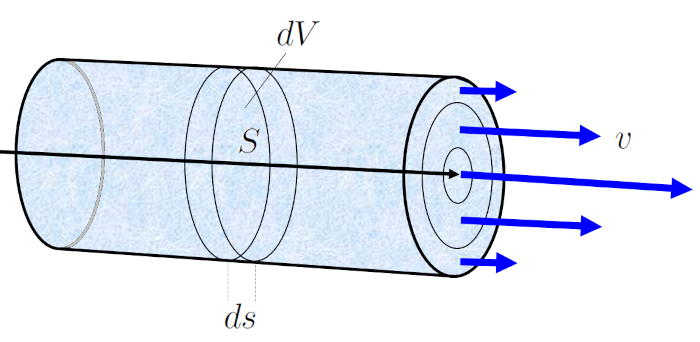
Dies erleichtert die Berechnung von der Volumenelement ($\Delta V$), dem Volumen der Flüssigkeit, das in einem bestimmten Zeitraum von der Abgelaufene Zeit ($\Delta t$) durch den Kanal fließt, entsprechend der Volumenstrom ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Volumenstrom und seine Geschwindigkeit
Konzept
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Es ist wichtig zu beachten, dass in diesem Modell:
Die Flussdichte als durchschnittliche Geschwindigkeit über den gesamten Querschnitt des Flusses wirkt.
ID:(15715, 0)
Fluss zu und von mehreren Kanälen
Konzept
Betrachtet man ein Rohr ohne Lecks oder zusätzliche Flüssigkeitszufuhr, so ist der Zufluss durch der Anzahl der Kanäle 1 ($N_1$), mit einer Durchflussrate von der Volumenstrom 1 ($J_{V1}$) pro Abschnitt, gleich dem Ausfluss durch der Anzahl der Kanäle 2 ($N_2$), mit einer Durchflussrate von der Volumenstrom 2 ($J_{V2}$) pro Abschnitt:
| $ N_1 J_{V1} = N_2 J_{V2} $ |
Innerhalb eines Kanals oder Rohres treten oft Veränderungen im Querschnitt auf, sei es durch Verengung oder Erweiterung:
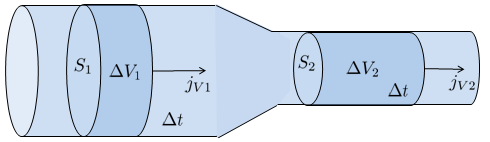
Diese Änderungen wirken sich direkt auf die Fließgeschwindigkeit aus, dargestellt durch die Flussdichte ($j_s$). Bei einer Verringerung des Querschnitts steigt die Geschwindigkeit, während bei einer Erweiterung die Geschwindigkeit sinkt, wie es die Rohr Sektion ($S$) erfordert, um der Volumenstrom ($J_V$) konstant zu halten, gemäß der folgenden Gleichung:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Die Erhaltung des Flusses, zusammen mit der Definition der Flussdichte, führt zum Erhaltungsgesetz, bei dem der Anzahl der Kanäle 1 ($N_1$), der Anzahl der Kanäle 2 ($N_2$), die Abschnitt in Punkt 1 ($S_1$), die Abschnitt in Punkt 2 ($S_2$), die Flussdichte 1 ($j_{s1}$) und die Flussdichte 2 ($j_{s2}$) folgende Bedingungen erfüllen:
| $ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $ |
ID:(15915, 0)
Gültigkeit der Kontinuitätsgleichung
Konzept
Die Kontinuitätsgleichung setzt voraus, dass der Fluss gleichmäßig ist und keine Rückflüsse oder Turbulenzen auftreten. Daher ist es notwendig sicherzustellen, dass der Fluss tatsächlich laminar ist und keine Turbulenzen aufweist, insbesondere wenn die Gleichung zur Analyse von Fluidströmungen in Rohren und Kanälen verwendet wird.
Es gibt verschiedene Methoden zur Erkennung von Turbulenzen im Fluss, wie die Verwendung von Durchflussmessern oder die visuelle Beobachtung des Flusses. Es ist unerlässlich, sicherzustellen, dass der Fluss stabil ist, bevor die Kontinuitätsgleichung angewendet wird, da jede Störung im Fluss die Genauigkeit der Berechnungen und die Gesamteffizienz des Systems beeinträchtigen kann.
ID:(978, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta V_1 = S_1 \Delta s_1 $
DV = S * Ds
$ \Delta V_2 = S_2 \Delta s_2 $
DV = S * Ds
$ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$
J_V = DV / Dt
$ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$
J_V = DV / Dt
$ N_1 J_{V1} = N_2 J_{V2} $
N_1 * J_V1 = N_2 * J_V2
$ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $
N_1 * S_1 * j_s1 = N_2 * S_2 * j_s2
$ S_1 = \pi r_1 ^2$
S = pi * r ^2
$ S_2 = \pi r_2 ^2$
S = pi * r ^2
ID:(15914, 0)
Volumenelement (1)
Gleichung
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
| $ \Delta V_1 = S_1 \Delta s_1 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 1)
Volumenelement (2)
Gleichung
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
| $ \Delta V_2 = S_2 \Delta s_2 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 2)
Mittlerer Volumenstrom (1)
Gleichung
Der Volumenstrom ($J_V$) entspricht der Volume Fließende ($\Delta V$), das durch den Kanal bei der Abgelaufene Zeit ($\Delta t$) fließt. Daher haben wir:
| $ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 1)
Mittlerer Volumenstrom (2)
Gleichung
Der Volumenstrom ($J_V$) entspricht der Volume Fließende ($\Delta V$), das durch den Kanal bei der Abgelaufene Zeit ($\Delta t$) fließt. Daher haben wir:
| $ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 2)
Durchschnittliche Strömungsdichte (1)
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$), was die Strecke ist, die die Flüssigkeit in der Abgelaufene Zeit ($\Delta t$) zurücklegt, wie folgt:
| $ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 1)
Durchschnittliche Strömungsdichte (2)
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$), was die Strecke ist, die die Flüssigkeit in der Abgelaufene Zeit ($\Delta t$) zurücklegt, wie folgt:
| $ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 2)
Volumenstrom und seine Geschwindigkeit (1)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Volumenstrom und seine Geschwindigkeit (2)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Volumenerhaltung mit mehreren Kanälen
Gleichung
Wenn die Dichte konstant bleibt, gilt das gleiche Prinzip für das Volumen. In solchen Fällen, wenn wir den Fluss als einen nicht komprimierbaren Stoff behandeln, sprechen wir von einem inkompressiblen Fluid. Mit anderen Worten, wenn ein bestimmtes Volumen von einem Ende durch mehrere Rohre eintritt, muss das gleiche Volumen am anderen Ende austreten, verteilt auf die Auslassrohre. Dies lässt sich durch die Gleichung ausdrücken, in der der Anzahl der Kanäle 1 ($N_1$) mit der Fließen in Position 1 ($J_1$) multipliziert wird und gleich der Anzahl der Kanäle 2 ($N_2$) mal der Fließen in Position 2 ($J_2$) ist, was zur folgenden Gleichung führt:
| $ N_1 J_{V1} = N_2 J_{V2} $ |
ID:(15912, 0)
Kontinuität für mehrere Abschnitte
Gleichung
Das Kontinuitätsprinzip besagt, dass der Fluss am Einlass, gegeben durch das Produkt von der Anzahl der Kanäle 1 ($N_1$), die Flussdichte 1 ($j_{s1}$) und die Abschnitt in Punkt 1 ($S_1$), gleich dem Fluss am Auslass sein muss, dargestellt durch das Produkt von der Anzahl der Kanäle 2 ($N_2$), die Flussdichte 2 ($j_{s2}$) und die Abschnitt in Punkt 2 ($S_2$). Daraus ergibt sich, dass:
kyon
ID:(15911, 0)
Oberfläche einer Scheibe (1)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_1 = \pi r_1 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Oberfläche einer Scheibe (2)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_2 = \pi r_2 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)