Utilisateur:
Écoulement d'un liquide à plusieurs canaux
Storyboard 
Dans le cas d'un flux provenant de plusieurs canaux qui se divise ensuite en plusieurs autres canaux égaux, la conservation du débit stipule que la somme des débits des canaux d'entrée doit être égale à la somme des débits des canaux de sortie. Ce principe découle directement de l'équation de continuité, qui garantit que le débit volumétrique total est conservé. Les mêmes concepts et équations utilisés pour un canal unique avec une section variable, comme la relation entre la vitesse et la surface, restent valables dans ce cas. En supposant que les canaux soient égaux, les calculs sont simplifiés, permettant une répartition uniforme du débit entre eux.
ID:(2097, 0)
Flux volumique
Concept
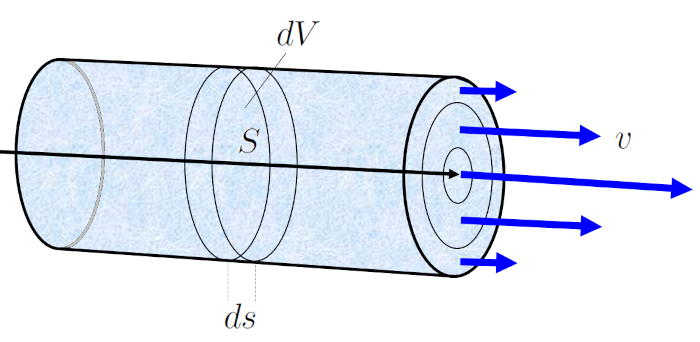
Durant un temps écoulé ($\Delta t$), le fluide avec une vitesse moyenne du fluide ($v$) se déplace de un élément tubulaire ($\Delta s$). Si a section ($S$) représente la quantité de fluide traversant cette section en le temps écoulé ($\Delta t$), elle se calcule comme suit :
$\Delta V = S \Delta s = Sv \Delta t$
Cette équation indique que le volume de fluide qui s'écoule à travers la section a section ($S$) durant un temps écoulé ($\Delta t$) est égal au produit de la surface de la section et de la distance parcourue par le fluide pendant ce temps.
Cela facilite le calcul de le élément de volume ($\Delta V$), qui est le volume de fluide s'écoulant à travers le canal sur une période spécifique de le temps écoulé ($\Delta t$), correspondant à Le volumique flux ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Flux volumique et sa vitesse
Concept
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Il est important de noter que dans ce modèle :
La densité de flux joue le rôle d'une vitesse moyenne sur toute la section du flux.
ID:(15715, 0)
Flux vers et depuis plusieurs canaux
Concept
Considerando um tubo sem vazamentos ou adições de líquido, o fluxo de entrada através de le nombre de canaux 1 ($N_1$), com uma taxa de fluxo de le volumique flux 1 ($J_{V1}$) por seção, será igual ao fluxo de saída através de le nombre de canaux 2 ($N_2$), com uma taxa de fluxo de le volumique flux 2 ($J_{V2}$) por seção:
| $ N_1 J_{V1} = N_2 J_{V2} $ |
Dentro de um canal ou tubo, é comum ocorrer variações na área da seção transversal, seja por ampliação ou redução:
Essas variações impactam diretamente a velocidade do fluxo, representada por a densité de flux ($j_s$). Se a área da seção transversal diminui, a velocidade aumenta, e se a área aumenta, a velocidade diminui, de acordo com a section de tube ($S$), para manter le volumique flux ($J_V$) constante, conforme indicado pela seguinte equação:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
A conservação do fluxo, juntamente com a definição da densidade do fluxo, resulta na lei de conservação, onde le nombre de canaux 1 ($N_1$), le nombre de canaux 2 ($N_2$), a section au point 1 ($S_1$), a section au point 2 ($S_2$), a densité de flux 1 ($j_{s1}$) e a densité de flux 2 ($j_{s2}$) atendem à condição:
| $ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $ |
ID:(15915, 0)
Validité de l'équation de continuité
Concept
L'équation de continuité suppose que l\'écoulement soit uniforme, sans reflux ou turbulence présents. Par conséquent, il est nécessaire de vérifier si l\'écoulement est réellement laminaire et exempt de turbulences, surtout lors de l\'application de l\'équation pour analyser l\'écoulement des fluides dans des tuyaux et des canaux.
Il existe plusieurs méthodes pour détecter les turbulences dans l\'écoulement, telles que l\'utilisation de débitmètres ou l\'observation visuelle de l\'écoulement. Il est essentiel de s\'assurer que l\'écoulement est stable avant d\'appliquer l\'équation de continuité, car toute perturbation dans l\'écoulement peut affecter la précision des calculs et l\'efficacité globale du système.
ID:(978, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta V_1 = S_1 \Delta s_1 $
DV = S * Ds
$ \Delta V_2 = S_2 \Delta s_2 $
DV = S * Ds
$ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$
J_V = DV / Dt
$ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$
J_V = DV / Dt
$ N_1 J_{V1} = N_2 J_{V2} $
N_1 * J_V1 = N_2 * J_V2
$ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $
N_1 * S_1 * j_s1 = N_2 * S_2 * j_s2
$ S_1 = \pi r_1 ^2$
S = pi * r ^2
$ S_2 = \pi r_2 ^2$
S = pi * r ^2
ID:(15914, 0)
Élément de volume (1)
Équation
Si nous avons un tube avec une a section de tube ($S$) se déplaçant sur une distance le élément tubulaire ($\Delta s$) le long de son axe, ayant déplacé Le élément de volume ($\Delta V$), alors cela é égal à :
| $ \Delta V_1 = S_1 \Delta s_1 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 1)
Élément de volume (2)
Équation
Si nous avons un tube avec une a section de tube ($S$) se déplaçant sur une distance le élément tubulaire ($\Delta s$) le long de son axe, ayant déplacé Le élément de volume ($\Delta V$), alors cela é égal à :
| $ \Delta V_2 = S_2 \Delta s_2 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 2)
Débit moyen (1)
Équation
Le volumique flux ($J_V$) correspond à Le volume fluide ($\Delta V$) qui s'écoule à travers le canal en le temps écoulé ($\Delta t$). Par conséquent, nous avons :
| $ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 1)
Débit moyen (2)
Équation
Le volumique flux ($J_V$) correspond à Le volume fluide ($\Delta V$) qui s'écoule à travers le canal en le temps écoulé ($\Delta t$). Par conséquent, nous avons :
| $ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 2)
Densité de flux moyenne (1)
Équation
A densité de flux ($j_s$) est lié à A distance parcourue en un temps ($\Delta s$), qui est la distance parcourue par le fluide dans le temps écoulé ($\Delta t$), comme suit :
| $ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 1)
Densité de flux moyenne (2)
Équation
A densité de flux ($j_s$) est lié à A distance parcourue en un temps ($\Delta s$), qui est la distance parcourue par le fluide dans le temps écoulé ($\Delta t$), comme suit :
| $ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 2)
Flux volumique et sa vitesse (1)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Flux volumique et sa vitesse (2)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Conservation du volume avec plusieurs canaux
Équation
Si la densité reste constante, le même principe s'applique au volume. Dans ces cas, lorsque nous traitons le flux comme un fluide incompressible, nous parlons d'un fluide incompressible. Autrement dit, si un certain volume entre par une extrémité à travers plusieurs tuyaux, le même volume doit sortir par l'autre extrémité, réparti entre les tuyaux de sortie. Cela peut être exprimé par l'égalité entre le nombre de canaux 1 ($N_1$) multiplié par le flux en position 1 ($J_1$) et le nombre de canaux 2 ($N_2$) multiplié par le flux en position 2 ($J_2$), ce qui donne l'équation suivante :
| $ N_1 J_{V1} = N_2 J_{V2} $ |
ID:(15912, 0)
Continuité pour plusieurs sections
Équation
Le principe de continuité stipule que le débit à l'entrée, donné par le produit de le nombre de canaux 1 ($N_1$), a densité de flux 1 ($j_{s1}$) et a section au point 1 ($S_1$), doit être égal au débit à la sortie, représenté par le produit de le nombre de canaux 2 ($N_2$), a densité de flux 2 ($j_{s2}$) et a section au point 2 ($S_2$). De cette équation, il découle que :
| $ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $ |
ID:(15911, 0)
Surface d'un disque (1)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_1 = \pi r_1 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Surface d'un disque (2)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_2 = \pi r_2 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)