User:
Flow of a liquid with multiple channels
Storyboard 
In the case of a flow coming from multiple channels and splitting into other multiple equal channels, the conservation of flow states that the sum of the flow rates in the initial channels must equal the sum of the flow rates in the final channels. This principle is derived directly from the continuity equation, which ensures that the total volumetric flow is conserved. The same concepts and equations that apply to a single channel with a variable cross-section, such as the relationship between velocity and area, remain valid in this scenario. By assuming that the channels are equal, the calculation is simplified, allowing for the uniform distribution of flow between them.
ID:(2097, 0)
Volume flow
Concept
During a time elapsed ($\Delta t$), the fluid with a mean Speed of Fluid ($v$) moves a tube element ($\Delta s$). If the section ($S$) represents the amount of fluid crossing that section in the time elapsed ($\Delta t$), it is calculated as:
$\Delta V = S \Delta s = Sv \Delta t$
This equation states that the volume of fluid flowing through section the section ($S$) during a time elapsed ($\Delta t$) is equal to the product of the cross-sectional area and the distance the fluid travels during that time.
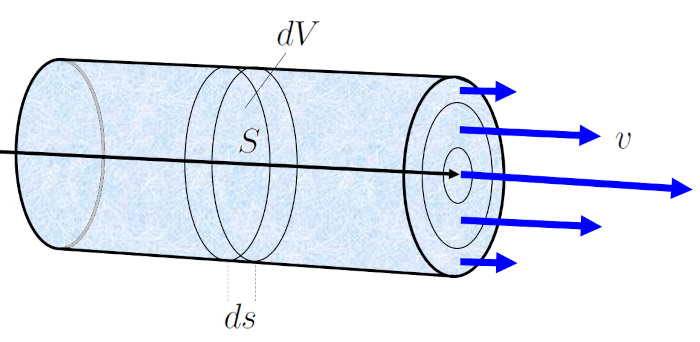
This facilitates the calculation of the volume element ($\Delta V$), which is the volume of fluid flowing through the channel in a specific period of the time elapsed ($\Delta t$), corresponding to the volume flow ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Volume Flow and its Speed
Concept
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
It is important to note that in this model:
The flow density acts as an average velocity across the entire flow section.
ID:(15715, 0)
Flow to and from multiple channels
Concept
Considering a tube with no leaks or additional liquid, the inflow through the number of channels 1 ($N_1$), with a flow rate of the volume flow 1 ($J_{V1}$) per section, will be equal to the outflow through the number of channels 2 ($N_2$), with a flow rate of the volume flow 2 ($J_{V2}$) per section:
| $ N_1 J_{V1} = N_2 J_{V2} $ |
Inside a channel or pipe, variations in cross-sectional area are common, whether by expansion or contraction:
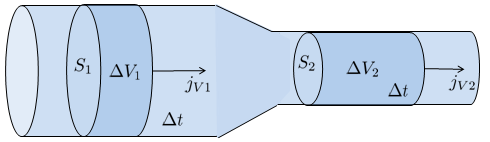
These changes directly affect the velocity of the fluid flow, represented by the flux density ($j_s$). If the cross-sectional area decreases, the velocity increases, and if the area increases, the velocity decreases, as determined by the section Tube ($S$) to keep the volume flow ($J_V$) constant, according to the following equation:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
The conservation of flow, combined with the definition of flow density, results in the conservation law, where the number of channels 1 ($N_1$), the number of channels 2 ($N_2$), the section in point 1 ($S_1$), the section in point 2 ($S_2$), the flux density 1 ($j_{s1}$), and the flux density 2 ($j_{s2}$) satisfy:
| $ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $ |
ID:(15915, 0)
Validity of Continuity Equation
Concept
The continuity equation assumes that the flow is uniform, with no reverse flows or turbulence present. Therefore, it is necessary to verify that the flow is indeed laminar and free of turbulence, especially when applying the equation to analyze fluid flows in pipes and channels.
There are various methods for detecting turbulence in the flow, such as using flow meters or visually observing the flow. It is essential to ensure that the flow is stable before applying the continuity equation, as any disturbance in the flow can affect the accuracy of the calculations and the overall efficiency of the system.
ID:(978, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta V_1 = S_1 \Delta s_1 $
DV = S * Ds
$ \Delta V_2 = S_2 \Delta s_2 $
DV = S * Ds
$ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$
J_V = DV / Dt
$ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$
J_V = DV / Dt
$ N_1 J_{V1} = N_2 J_{V2} $
N_1 * J_V1 = N_2 * J_V2
$ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $
N_1 * S_1 * j_s1 = N_2 * S_2 * j_s2
$ S_1 = \pi r_1 ^2$
S = pi * r ^2
$ S_2 = \pi r_2 ^2$
S = pi * r ^2
ID:(15914, 0)
Volume element (1)
Equation
If we have a tube with a the section Tube ($S$) moving a distance the tube element ($\Delta s$) along its axis, having displaced the volume element ($\Delta V$), then it is equal to:
| $ \Delta V_1 = S_1 \Delta s_1 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 1)
Volume element (2)
Equation
If we have a tube with a the section Tube ($S$) moving a distance the tube element ($\Delta s$) along its axis, having displaced the volume element ($\Delta V$), then it is equal to:
| $ \Delta V_2 = S_2 \Delta s_2 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 2)
Mean volume flow (1)
Equation
The volume flow ($J_V$) corresponds to the volume flowing ($\Delta V$) flowing through the channel at the time elapsed ($\Delta t$). Therefore, we have:
| $ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 1)
Mean volume flow (2)
Equation
The volume flow ($J_V$) corresponds to the volume flowing ($\Delta V$) flowing through the channel at the time elapsed ($\Delta t$). Therefore, we have:
| $ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 2)
Average flow density (1)
Equation
The flux density ($j_s$) is related to the distance traveled in a time ($\Delta s$), which is the distance that the fluid travels in the time elapsed ($\Delta t$), as follows:
| $ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 1)
Average flow density (2)
Equation
The flux density ($j_s$) is related to the distance traveled in a time ($\Delta s$), which is the distance that the fluid travels in the time elapsed ($\Delta t$), as follows:
| $ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 2)
Volume Flow and its Speed (1)
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Volume Flow and its Speed (2)
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Volume conservation with multiple channels
Equation
If the density remains constant, the same principle applies to volume. In these cases, when we treat the flow as an incompressible fluid, we refer to it as an incompressible fluid. In other words, if a certain volume enters from one end through multiple tubes, the same amount of volume must exit from the other end, distributed across the output tubes. This can be expressed by the equality between the number of channels 1 ($N_1$) multiplied by the flow in Position 1 ($J_1$) and the number of channels 2 ($N_2$) multiplied by the flow in Position 2 ($J_2$), resulting in the following equation:
| $ N_1 J_{V1} = N_2 J_{V2} $ |
ID:(15912, 0)
Continuity for multiple sections
Equation
The continuity principle states that the flow at the inlet, given by the product of the number of channels 1 ($N_1$), the flux density 1 ($j_{s1}$), and the section in point 1 ($S_1$), must be equal to the flow at the outlet, represented by the product of the number of channels 2 ($N_2$), the flux density 2 ($j_{s2}$), and the section in point 2 ($S_2$). From this, it follows that:
| $ N_1 S_1 j_{s1} = N_2 S_2 j_{s2} $ |
ID:(15911, 0)
Surface of a disk (1)
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S_1 = \pi r_1 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Surface of a disk (2)
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S_2 = \pi r_2 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)