Utilisateur:
Écoulement d'un liquide incompressible
Storyboard 
Lorsqu'un liquide est en mouvement, on parle de flux, et sa mesure est basée sur le volume qui traverse une section en un laps de temps donné. En supposant que le volume se déplace sans se déformer, la vitesse à laquelle le liquide passe à travers la section reste constante. Dans ce cas, le flux peut également être défini comme le produit de la vitesse et de la section transversale.
ID:(875, 0)
Flux volumique
Concept
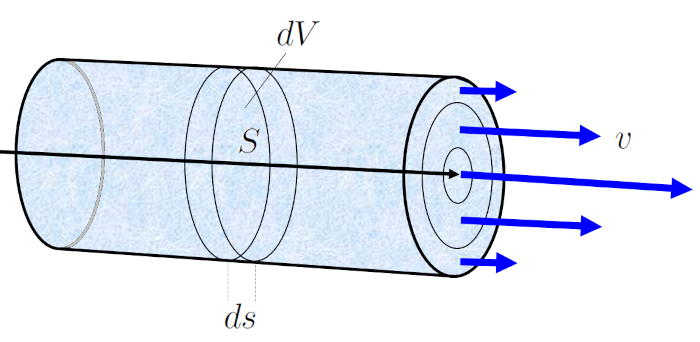
Durant un temps écoulé ($\Delta t$), le fluide avec une vitesse moyenne du fluide ($v$) se déplace de un élément tubulaire ($\Delta s$). Si a section ($S$) représente la quantité de fluide traversant cette section en le temps écoulé ($\Delta t$), elle se calcule comme suit :
$\Delta V = S \Delta s = Sv \Delta t$
Cette équation indique que le volume de fluide qui s'écoule à travers la section a section ($S$) durant un temps écoulé ($\Delta t$) est égal au produit de la surface de la section et de la distance parcourue par le fluide pendant ce temps.
Cela facilite le calcul de le élément de volume ($\Delta V$), qui est le volume de fluide s'écoulant à travers le canal sur une période spécifique de le temps écoulé ($\Delta t$), correspondant à Le volumique flux ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Flux volumique et sa vitesse
Concept
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Il est important de noter que dans ce modèle :
La densité de flux joue le rôle d'une vitesse moyenne sur toute la section du flux.
ID:(15715, 0)
Canal à section variable
Concept
En considérant un tube qui ne fuit pas et auquel aucun liquide n'est ajouté, le flux entrant à un point 1 Le volumique flux 1 ($J_{V1}$) sera égal à celui sortant à un point 2 Le volumique flux 2 ($J_{V2}$) :
| $ J_{V1} = J_{V2} $ |
Au sein d'un canal ou d'un tube, il peut y avoir un changement de section, soit par élargissement, soit par rétrécissement.
Cette variation affectera directement le flux à travers a densité de flux ($j_s$), qui représente la vitesse, augmentant (si la section se rétrécit) ou diminuant (si elle s'élargit) selon a section de tube ($S$) pour maintenir le volumique flux ($J_V$) constant, comme l'indique :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
La conservation du flux, associée à la définition de la densité de flux, conduit à la loi de conservation telle que a section au point 1 ($S_1$), a section au point 2 ($S_2$), a densité de flux 1 ($j_{s1}$) et a densité de flux 2 ($j_{s2}$) satisfont :
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(2213, 0)
Validité de l'équation de continuité
Concept
L'équation de continuité suppose que l\'écoulement soit uniforme, sans reflux ou turbulence présents. Par conséquent, il est nécessaire de vérifier si l\'écoulement est réellement laminaire et exempt de turbulences, surtout lors de l\'application de l\'équation pour analyser l\'écoulement des fluides dans des tuyaux et des canaux.
Il existe plusieurs méthodes pour détecter les turbulences dans l\'écoulement, telles que l\'utilisation de débitmètres ou l\'observation visuelle de l\'écoulement. Il est essentiel de s\'assurer que l\'écoulement est stable avant d\'appliquer l\'équation de continuité, car toute perturbation dans l\'écoulement peut affecter la précision des calculs et l\'efficacité globale du système.
ID:(978, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta V_1 = S_1 \Delta s_1 $
DV = S * Ds
$ \Delta V_2 = S_2 \Delta s_2 $
DV = S * Ds
$ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$
J_V = DV / Dt
$ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$
J_V = DV / Dt
$ J_{V1} = J_{V2} $
J_V1 = J_V2
$ S_1 = \pi r_1 ^2$
S = pi * r ^2
$ S_2 = \pi r_2 ^2$
S = pi * r ^2
$ S_1 j_{s1} = S_2 j_{s2} $
S_1 * j_s1 = S_2 * j_s2
ID:(15488, 0)
Élément de volume (1)
Équation
Si nous avons un tube avec une a section de tube ($S$) se déplaçant sur une distance le élément tubulaire ($\Delta s$) le long de son axe, ayant déplacé Le élément de volume ($\Delta V$), alors cela é égal à :
| $ \Delta V_1 = S_1 \Delta s_1 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 1)
Élément de volume (2)
Équation
Si nous avons un tube avec une a section de tube ($S$) se déplaçant sur une distance le élément tubulaire ($\Delta s$) le long de son axe, ayant déplacé Le élément de volume ($\Delta V$), alors cela é égal à :
| $ \Delta V_2 = S_2 \Delta s_2 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 2)
Débit moyen (1)
Équation
Le volumique flux ($J_V$) correspond à Le volume fluide ($\Delta V$) qui s'écoule à travers le canal en le temps écoulé ($\Delta t$). Par conséquent, nous avons :
| $ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 1)
Débit moyen (2)
Équation
Le volumique flux ($J_V$) correspond à Le volume fluide ($\Delta V$) qui s'écoule à travers le canal en le temps écoulé ($\Delta t$). Par conséquent, nous avons :
| $ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 2)
Densité de flux moyenne (1)
Équation
A densité de flux ($j_s$) est lié à A distance parcourue en un temps ($\Delta s$), qui est la distance parcourue par le fluide dans le temps écoulé ($\Delta t$), comme suit :
| $ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 1)
Densité de flux moyenne (2)
Équation
A densité de flux ($j_s$) est lié à A distance parcourue en un temps ($\Delta s$), qui est la distance parcourue par le fluide dans le temps écoulé ($\Delta t$), comme suit :
| $ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 2)
Flux volumique et sa vitesse (1)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Flux volumique et sa vitesse (2)
Équation
Une densité de flux ($j_s$) peut être exprimé en termes de le volumique flux ($J_V$) à l'aide de a coupe ou surface ($S$) par la formule suivante :
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Le flux est défini comme le volume le élément de volume ($\Delta V$) divisé par le temps le temps écoulé ($\Delta t$), ce qui est exprimé dans l'équation suivante :
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
et le volume est égal à la section transversale a section de tube ($S$) multipliée par la distance parcourue le élément tubulaire ($\Delta s$) :
| $ \Delta V = S \Delta s $ |
Étant donné que la distance parcourue le élément tubulaire ($\Delta s$) par unité de temps le temps écoulé ($\Delta t$) correspond à la vitesse, elle est représentée par :
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Ainsi, le flux est une densité de flux ($j_s$), qui est calculé à l'aide de :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Débit volumique instantané
Équation
L'une des lois les plus fondamentales en physique est la conservation de la masse, qui est valable dans tout notre monde macroscopique. Seul le monde microscopique connaît une conversion entre masse et énergie, que nous ne considérerons pas dans ce cas. Dans le cas d'un fluide, cela signifie que la masse entrant par un tuyau doit être égale à celle qui en sort.
Si la densité est constante, cela s'applique également au volume. Dans de tels cas, lorsque nous traitons l'écoulement comme un fluide incompressible, cela signifie qu'un volume donné entrant par une extrémité du tuyau doit sortir par l'autre extrémité. Cela peut être exprimé par l'égalité entre le flux en position 1 ($J_1$) et le flux en position 2 ($J_2$), avec l'équation :
| $ J_{V1} = J_{V2} $ |
ID:(939, 0)
Surface d'un disque (1)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_1 = \pi r_1 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Surface d'un disque (2)
Équation
A section ($S$) de un rayon du disque ($r$) est calculée comme suit :
| $ S_2 = \pi r_2 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)
Débit volumique instantané
Équation
Le principe de continuité stipule que le débit au premier point, égal à A densité de flux 1 ($j_{s1}$) multiplié par a section au point 1 ($S_1$), doit être égal au débit au second point, donné par a densité de flux 2 ($j_{s2}$) multiplié par a section au point 2 ($S_2$). Il en résulte que :
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(4350, 0)