mechanisms

Se considerarmos o fluxo como uma s rie de volumes com lados $\Delta x$, $\Delta y$ e $\Delta z$ se movendo na corrente, podemos assumir que a energia contida neles se mant m constante. Isso significa que, se calculamos a densidade de energia em qualquer ponto, ela ser sempre a mesma.

image

Se o meio possui uma densidade $\rho$, a massa do volume $\Delta x\Delta y\Delta z$ pode ser calculada como:

$m=\rho\Delta x\Delta y\Delta z$

A partir disso, podemos estimar a energia cin tica do elemento utilizando a velocidade $v$:

$\displaystyle\frac{1}{2}m v^2=\displaystyle\frac{1}{2}\rho\Delta x\Delta y\Delta z v^2$

Isso pode ser visualizado na seguinte imagem:

image

Portanto, a densidade da energia cin tica

$\displaystyle\frac{m v^2}{2 \Delta x\Delta y\Delta z}=\displaystyle\frac{1}{2}\rho v^2$

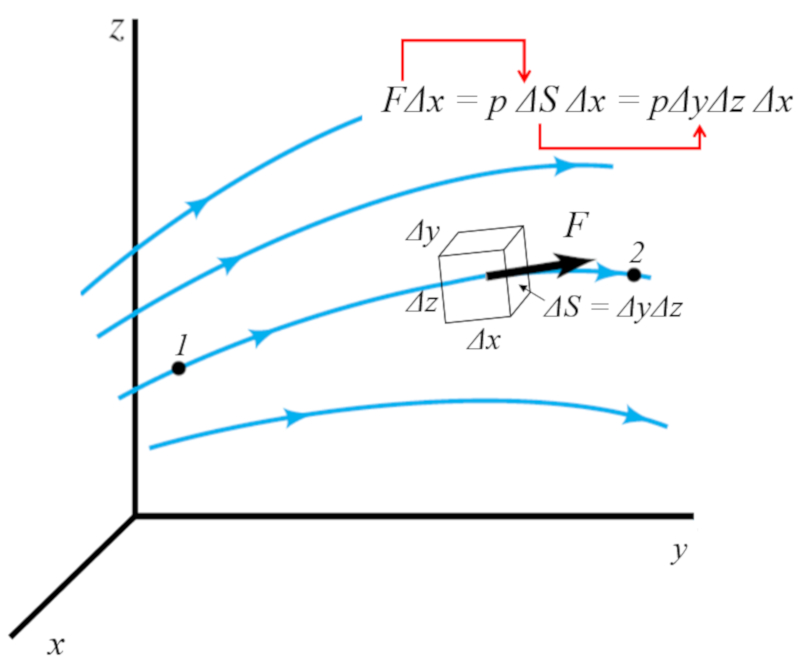
Si l'on suppose qu'il existe une force agissant sur l' l ment et si nous orientons le syst me de coordonn es de sorte que cette force agisse dans la direction x, alors la force effectuera un travail donn par :

$F\Delta x$

Si la force est g n r e par une pression, alors elle agira sur la surface perpendiculaire la direction de la force, c'est- -dire $\Delta y \Delta z$. Ainsi, l' nergie sera:

$F = p \Delta S = p \Delta y\Delta z$

Cela peut tre visualis dans l'image suivante :

image

Portanto, a densidade da energia potencial gravitacional

$\displaystyle\frac{mgh}{\Delta x\Delta y\Delta z}=\rho g h$

Se assumirmos que existe uma for a atuando no elemento e se orientarmos o sistema de coordenadas de forma que essa for a atue na dire o x, ent o a for a estar realizando um trabalho dado por:

$F\Delta x$

Se a for a for gerada por uma press o, ent o ela atuar na superf cie perpendicular dire o da for a, ou seja, $\Delta y \Delta z$. Portanto, a energia ser :

$F = p \Delta S = p \Delta y\Delta z$

Isso pode ser visualizado na seguinte imagem:

image

Portanto, a densidade da energia geral

$\displaystyle\frac{F \Delta x}{\Delta x\Delta y\Delta z}=\displaystyle\frac{p \Delta x\Delta y\Delta z}{\Delta x\Delta y\Delta z}=p$

A hip tese de Bernoulli postula que a energia conservada localmente, ou seja, n o existem mecanismos que permitam a um volume do meio trocar energia com o seu ambiente. Se analisarmos a equa o de energia $E$, que inclui:

• A energia cin tica em fun o da massa $m$ e la velocidade em um raio do cilindro ($v$),
• A energia potencial gravitacional dependente de la aceleração gravitacional ($g$) e la altura da coluna ($h$),
• Uma for a externa $F$ que impulsiona o l quido ao longo de uma dist ncia $\Delta z$,
podemos express -la da seguinte forma:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Considerando a energia em um volume $\Delta x\Delta y\Delta z$, podemos substituir a massa por la densidade ($\rho$):

$m=\rho \Delta x\Delta y\Delta z$

E dado que la pressão da coluna de água ($p$) definido como:

$F=p \Delta S =p \Delta y\Delta z$

Obtemos a equa o de la densidade de energia ($e$):

equation=3159

Em um contexto onde n o h viscosidade, a conserva o da energia sugere que la densidade de energia ($e$) se mant m constante em qualquer ponto do fluido. Assim, conhecer a velocidade e/ou a press o em um local determinado do fluido permite estabelecer uma rela o entre essas vari veis em qualquer outra parte do mesmo.

A hip tese da lei de Bernoulli que a energia, e consequentemente la densidade de energia ($e$), permanece constante. Nesse caso, a densidade de energia a soma de:

• Energia cin tica, que depende de la densidade líquida ($\rho_w$) e la velocidade em um raio do cilindro ($v$),
• Energia potencial gravitacional, que depende de la aceleração gravitacional ($g$) e la altura da coluna ($h$),
• Energia potencial em geral, que depende de la pressão ($p$),
resultando em:

equation=3159

No entanto, isso limita a aplicabilidade da lei porque:

• A viscosidade um processo no qual a energia se difunde pelo meio e, nesse sentido, a energia n o conservada localmente, pois redistribu da no meio.

• V rtices n o podem existir, pois eles inerentemente t m zonas de diferentes densidades de energia, o que vai contra a hip tese. Isso significa que n o descreveria um fluxo turbulento.

O problema que na maioria dos casos, o fluxo pode ser dominado pela viscosidade, chamado de fluxo laminar, ou pela in rcia, observado como fluxo turbulento. Portanto, a lei de Bernoulli um modelo aplic vel apenas em situa es em que a inomogeneidade da densidade de energia menor.

Se assumirmos que la densidade de energia ($e$) conservado, podemos afirmar que para uma c lula onde a velocidade m dia la velocidade em um raio do cilindro ($v$), a densidade la densidade ($\rho$), a press o la pressão da coluna de água ($p$), a altura la altura da coluna ($h$) e a acelera o gravitacional la aceleração gravitacional ($g$), temos o seguinte:

equation=3159

Em um ponto 1, essa equa o ser igual mesma equa o em um ponto 2:

$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$

onde la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representam a velocidade, altura e press o no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representam a velocidade, altura e press o no ponto 2, respectivamente.

Portanto, temos a equa o de Bernoulli [1]:

equation=4504

[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)

importante ter em mente as seguintes suposi es:

A energia conservada, especialmente assumindo a aus ncia de viscosidade.

N o h deforma o no meio, portanto, a densidade permanece constante.

N o h vorticidade, ou seja, n o h redemoinhos que gerem circula o no meio. O fluido deve exibir um comportamento laminar.

Nos dispensadores de perfume, criado um fluxo de ar sobre um tubo imerso no perfume. Isso faz com que a press o diminua, resultando em uma press o menor na coluna de perfume em rela o coluna gerada pelo l quido dentro do frasco. Como resultado, o l quido impulsionado atrav s da coluna. No final, o l quido que chega parte superior pulverizado e transportado pelo jato de ar.

image

Para modelar o sistema, pode-se utilizar a lei de Bernoulli com a densidade do l quido la densidade líquida ($\rho_w$) e a altura la aceleração gravitacional ($g$). Se o ponto 1 estiver na base do tubo de transporte do l quido, ent o la velocidade média do fluido no ponto 1 ($v_1$) nulo, la hauteur ou profondeur 1 ($h_1$) a profundidade do l quido ($h$), e la pressão na coluna 1 ($p_1$) a press o atmosf rica. Se o ponto 2 estiver na sa da superior do tubo de transporte do l quido, ent o la velocidade média do fluido no ponto 2 ($v_2$) a velocidade com que o l quido emerge ($v$), la hauteur ou profondeur 2 ($h_2$) nulo, e la pressão na coluna 2 ($p_2$) a press o atmosf rica. Portanto, a express o

equation=4504

se reduz a

$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $

pois a press o atmosf rica simplificada. Com isso, a velocidade com que o l quido emerge :

$v = \sqrt{ 2 g h }$

model

Se a energia for conservada dentro dos volumes que fluem com o fluxo, ent o la densidade de energia em 1 ($e_1$) e la densidade de energia em 2 ($e_2$) devem ser iguais:

kyon

Isso s poss vel se a viscosidade for negligenci vel, pois ela est associada difus o de energia, e n o h v rtices presentes, os quais apresentam diferen as de energia devido s velocidades tangenciais variadas ao longo do raio do v rtice.

Uma vez que um fluido ou g s um cont nuo, o conceito de energia j n o pode ser associado a uma massa espec fica. No entanto, poss vel considerar a energia contida num volume do cont nuo e, ao dividir pela pr pria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade em um raio do cilindro ($v$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão da coluna de água ($p$), temos:

kyon

o que corresponde equa o de Bernoulli.

Uma vez que um fluido ou g s um cont nuo, o conceito de energia j n o pode ser associado a uma massa espec fica. No entanto, poss vel considerar a energia contida num volume do cont nuo e, ao dividir pela pr pria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade em um raio do cilindro ($v$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão da coluna de água ($p$), temos:

kyon

o que corresponde equa o de Bernoulli.

Com la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representando a velocidade, altura e press o no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representando a velocidade, altura e press o no ponto 2, respectivamente, temos:

kyon

A diferen a de altura, representada por la diferença de altura ($\Delta h$), implica que a press o em ambas as colunas diferente. Em particular, la diferença de pressão ($\Delta p$) uma fun o de la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$) e la diferença de altura ($\Delta h$), da seguinte forma:

kyon

Quando duas colunas de l quido s o conectadas com la altura da coluna líquida 1 ($h_1$) e la altura da coluna líquida 2 ($h_2$), criada uma la diferença de altura ($\Delta h$), que calculada da seguinte forma:

kyon

A La diferença de altura ($\Delta h$) ir gerar a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.

Quando duas colunas de l quido s o conectadas com la pressão na coluna 1 ($p_1$) e la pressão na coluna 2 ($p_2$), criada uma la diferença de pressão ($\Delta p$) que calculada de acordo com a seguinte f rmula:

kyon

la diferença de pressão ($\Delta p$) representa a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.

La diferença de velocidade entre superfícies ($\Delta v$) est com la velocidade média do fluido no ponto 1 ($v_1$) e la velocidade média do fluido no ponto 2 ($v_2$)

kyon