Bernoulli avec pression hydrostatique
Storyboard 
Si nous considérons un fluide sans viscosité et sans turbulence (écoulement laminaire), nous pouvons supposer que l'énergie est conservée et circule avec le liquide (ou le gaz). Dans ces cas, nous obtenons une équation qui établit que la somme de la densité d'énergie cinétique et la densité d'énergie potentielle sont constantes.
Cela permet de calculer comment la vitesse évolue en fonction de la position dès lors que la pression existante ou tout champ de force est connu.
Le seul problème est que la plupart des milieux présentent une viscosité pertinente et, par conséquent, tendent à ne pas avoir de turbulence ou celle-ci est négligeable et l'écoulement est intrinsèquement turbulent. Par conséquent, l'application de la loi de Bernoulli est dans ce sens restreinte, ou plutôt une première approximation.
ID:(684, 0)
Bernoulli avec pression hydrostatique
Storyboard 
Si nous considérons un fluide sans viscosité et sans turbulence (écoulement laminaire), nous pouvons supposer que l'énergie est conservée et circule avec le liquide (ou le gaz). Dans ces cas, nous obtenons une équation qui établit que la somme de la densité d'énergie cinétique et la densité d'énergie potentielle sont constantes. Cela permet de calculer comment la vitesse évolue en fonction de la position dès lors que la pression existante ou tout champ de force est connu. Le seul problème est que la plupart des milieux présentent une viscosité pertinente et, par conséquent, tendent à ne pas avoir de turbulence ou celle-ci est négligeable et l'écoulement est intrinsèquement turbulent. Par conséquent, l'application de la loi de Bernoulli est dans ce sens restreinte, ou plutôt une première approximation.
Variables
Calculs
Calculs
Équations
Une autre quation utile est celle correspondant la conservation de l' nergie, qui s'applique dans les cas o la viscosit , un processus entra nant une perte d' nergie, peut tre n glig e. Si l'on consid re l' quation classique de l' nergie $E$, qui prend en compte l\' nergie cin tique, l\' nergie potentielle gravitationnelle et une force externe d pla ant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la mani re suivante :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si l\'on consid re l\' nergie l\'int rieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :
$m=\rho \Delta x\Delta y\Delta z$
Et puisque la pression est donn e par :
$F=p \Delta S =p \Delta y\Delta z$
On obtient l\' quation de la densit d\' nergie :
Une autre quation utile est celle correspondant la conservation de l' nergie, qui s'applique dans les cas o la viscosit , un processus entra nant une perte d' nergie, peut tre n glig e. Si l'on consid re l' quation classique de l' nergie $E$, qui prend en compte l\' nergie cin tique, l\' nergie potentielle gravitationnelle et une force externe d pla ant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la mani re suivante :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si l\'on consid re l\' nergie l\'int rieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :
$m=\rho \Delta x\Delta y\Delta z$
Et puisque la pression est donn e par :
$F=p \Delta S =p \Delta y\Delta z$
On obtient l\' quation de la densit d\' nergie :
S'il existe a différence de pression ($\Delta p$) entre deux points, comme le d termine l' quation :
nous pouvons utiliser a pression de la colonne d'eau ($p$), qui est d finie comme suit :
Cela donne :
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Comme a différence de hauteur ($\Delta h$) est d finie comme suit :
a différence de pression ($\Delta p$) peut tre exprim e comme suit :
Si nous supposons que a densité d'énergie ($e$) est conserv , alors pour une cellule o la vitesse moyenne est a vitesse dans un rayon du cylindre ($v$), la densit est a densité ($\rho$), la pression est a pression de la colonne d'eau ($p$), la hauteur est a hauteur de la colonne ($h$), et l'acc l ration gravitationnelle est a accélération gravitationnelle ($g$), nous avons ce qui suit :
En un point 1, cette quation sera gale la m me quation en un point 2 :
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
o a vitesse moyenne du fluide au point 1 ($v_1$), a hauteur ou profondeur 1 ($h_1$) et a pression dans la colonne 1 ($p_1$) repr sentent la vitesse, la hauteur et la pression au point 1, respectivement, et a vitesse moyenne du fluide au point 2 ($v_2$), a hauteur ou profondeur 2 ($h_2$) et a pression dans la colonne 2 ($p_2$) repr sentent la vitesse, la hauteur et la pression au point 2, respectivement. Par cons quent, nous avons :
Exemples
Si nous envisageons l' coulement comme une s rie de volumes avec des c t s $\Delta x$, $\Delta y$ et $\Delta z$ se d pla ant dans le courant, nous pouvons supposer que l' nergie qu'ils contiennent reste constante. Cela signifie que si nous calculons la densit d\' nergie en n\'importe quel point, elle sera toujours la m me.
Si le milieu a une densit de $\rho$, la masse du volume $\Delta x\Delta y\Delta z$ peut tre calcul e comme suit :
$m=\rho\Delta x\Delta y\Delta z$
partir de l , nous pouvons estimer l' nergie cin tique de l' l ment en utilisant la vitesse $v$:
$\displaystyle\frac{1}{2}m v^2=\displaystyle\frac{1}{2}\rho\Delta x\Delta y\Delta z v^2$
Cela peut tre visualis dans l'image suivante :
Par cons quent, la densit de l' nergie cin tique est
$\displaystyle\frac{m v^2}{2 \Delta x\Delta y\Delta z}=\displaystyle\frac{1}{2}\rho v^2$
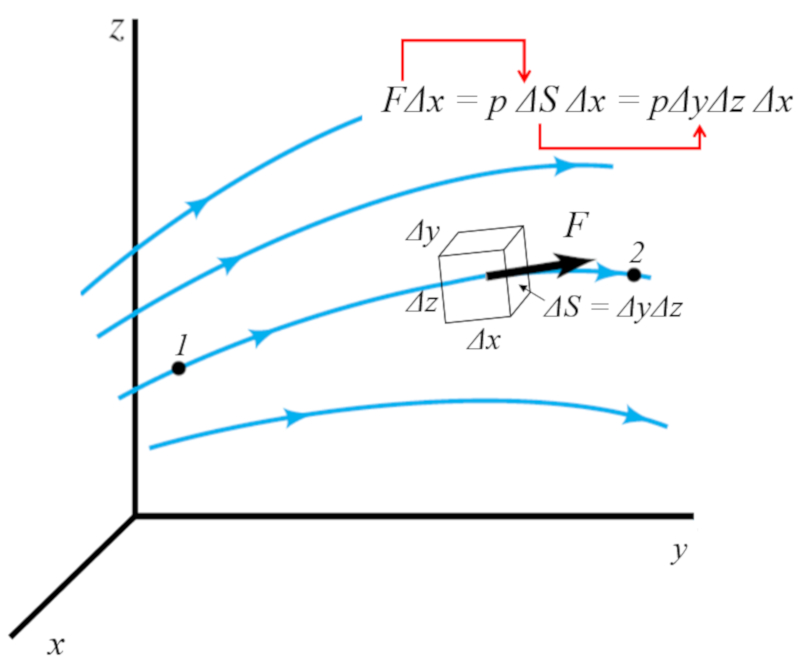
Si l'on suppose qu'il existe une force agissant sur l' l ment et si nous orientons le syst me de coordonn es de sorte que cette force agisse dans la direction x, alors la force effectue un travail donn par :
$F\Delta x$
Si la force est g n r e par une pression, alors elle agit sur la surface perpendiculaire la direction de la force, c'est- -dire $ \Delta y \Delta z$. Ainsi, l' nergie est donn e par :
$F = p \Delta S = p \Delta y\Delta z$
Cela peut tre visualis dans l'image suivante :
Par cons quent, la densit de l' nergie potentielle gravitationnelle est
$\displaystyle\frac{mgh}{\Delta x\Delta y\Delta z}=\rho g h$
Si l'on suppose qu'il existe une force agissant sur l' l ment et si nous orientons le syst me de coordonn es de sorte que cette force agisse dans la direction x, alors la force effectuera un travail donn par :
$F\Delta x$
Si la force est g n r e par une pression, alors elle agira sur la surface perpendiculaire la direction de la force, c'est- -dire $\Delta y \Delta z$. Ainsi, l' nergie sera :
$F = p \Delta S = p \Delta y\Delta z$
Cela peut tre visualis dans l'image suivante :
Par cons quent, la densit de l' nergie g n rale est
$\displaystyle\frac{F \Delta x}{\Delta x\Delta y\Delta z}=\displaystyle\frac{p \Delta x\Delta y\Delta z}{\Delta x\Delta y\Delta z}=p$
L'hypoth se de Bernoulli postule que l' nergie est conserv e localement, c'est- -dire qu'il n'y a pas de m canismes permettant un volume du milieu d' changer de l' nergie avec son environnement. Si nous consid rons l' quation de l' nergie $E$, qui inclut :
• L' nergie cin tique en fonction de la masse $m$ et a vitesse dans un rayon du cylindre ($v$),
• L' nergie potentielle gravitationnelle en fonction de a accélération gravitationnelle ($g$) et a hauteur de la colonne ($h$),
• Une force externe $F$ qui d place le liquide sur une distance $\Delta z$,
nous pouvons l'exprimer ainsi :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
En consid rant l' nergie dans un volume $\Delta x\Delta y\Delta z$, nous pouvons remplacer la masse par a densité ($\rho$) :
$m=\rho \Delta x\Delta y\Delta z$
Et comme a pression de la colonne d'eau ($p$) est exprim par :
$F=p \Delta S =p \Delta y\Delta z$
Nous obtenons l' quation de a densité d'énergie ($e$) :
En l'absence de viscosit , la conservation de l' nergie implique que a densité d'énergie ($e$) reste constante en tout point du fluide. Par cons quent, conna tre la vitesse et/ou la pression en un lieu donn du fluide suffit pour tablir une relation entre la vitesse et la pression en tout point du fluide.
L'hypoth se de la loi de Bernoulli est que l' nergie, et donc a densité d'énergie ($e$), reste constante. Dans ce cas, la densit d' nergie est la somme de :
• L' nergie cin tique, qui d pend de a densité du liquide ($\rho_w$) et a vitesse dans un rayon du cylindre ($v$),
• L' nergie potentielle gravitationnelle, qui d pend de a accélération gravitationnelle ($g$) et a hauteur de la colonne ($h$),
• L' nergie potentielle g n rale, qui d pend de a pression ($p$),
ce qui donne :
Cependant, cela limite l'applicabilit de la loi car :
• La viscosit est un processus dans lequel l' nergie se diffuse travers le milieu et, dans ce sens, l' nergie n'est pas conserv e localement car elle est redistribu e dans le milieu.
• Les tourbillons ne peuvent pas exister car ils ont inh remment des zones de densit s nerg tiques diff rentes, ce qui contredit l'hypoth se. Cela signifie qu'elle ne d crirait pas un coulement turbulent.
Le probl me est que dans la plupart des cas, l' coulement peut tre domin par la viscosit , appel coulement laminaire, ou par l'inertie, observ comme un coulement turbulent. Ainsi, la loi de Bernoulli est un mod le applicable uniquement dans des situations o l'inhomog n it de la densit d' nergie est moindre.
Si nous supposons que a densité d'énergie ($e$) est conserv , alors pour une cellule o la vitesse moyenne est a vitesse dans un rayon du cylindre ($v$), la densit est a densité ($\rho$), la pression est a pression de la colonne d'eau ($p$), la hauteur est a hauteur de la colonne ($h$), et l'acc l ration gravitationnelle est a accélération gravitationnelle ($g$), nous avons ce qui suit :
En un point 1, cette quation sera gale la m me quation en un point 2 :
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
o a vitesse moyenne du fluide au point 1 ($v_1$), a hauteur ou profondeur 1 ($h_1$) et a pression dans la colonne 1 ($p_1$) repr sentent la vitesse, la hauteur et la pression au point 1, respectivement, et a vitesse moyenne du fluide au point 2 ($v_2$), a hauteur ou profondeur 2 ($h_2$) et a pression dans la colonne 2 ($p_2$) repr sentent la vitesse, la hauteur et la pression au point 2, respectivement.
On a donc l quation de Bernoulli [1] :![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
Il est important de garder l'esprit les hypoth ses suivantes :
L' nergie est conserv e, en supposant notamment l\'absence de viscosit .
Il n\'y a pas de d formation du milieu, donc la densit reste constante.
Il n\'y a pas de vorticit , c\'est- -dire de tourbillons qui entra nent une circulation dans le milieu. Le fluide doit pr senter un comportement laminaire.
Dans les distributeurs de parfum, un courant d'air est g n r autour d'un tube immerg dans le parfum. Cela entra ne une baisse de pression, ce qui fait que la pression dans la colonne de parfum est inf rieure celle g n r e par le liquide l'int rieur du flacon, ce qui propulse le liquide travers la colonne. Finalement, le liquide qui atteint la partie sup rieure est pulv ris et transport par le jet d\'air.
Pour mod liser le syst me, on peut utiliser la loi de Bernoulli avec la densit du liquide a densité du liquide ($\rho_w$) et la hauteur a accélération gravitationnelle ($g$). Si le point 1 est la base du tube de transport du liquide, alors a vitesse moyenne du fluide au point 1 ($v_1$) est nul, a hauteur ou profondeur 1 ($h_1$) est la profondeur du liquide ($h$), et a pression dans la colonne 1 ($p_1$) est la pression atmosph rique. Si le point 2 est la sortie sup rieure du tube de transport du liquide, alors a vitesse moyenne du fluide au point 2 ($v_2$) est la vitesse laquelle le liquide merge ($v$), a hauteur ou profondeur 2 ($h_2$) est nul, et a pression dans la colonne 2 ($p_2$) est la pression atmosph rique. Par cons quent, l'expression
se r duit
$\rho g h=\displaystyle\frac{1}{2}\rho v^2 $
car la pression atmosph rique est simplifi e. Ainsi, la vitesse laquelle le liquide merge est :
$v = \sqrt{ 2 g h }$
Si l' nergie est conserv e au sein des volumes en coulement, alors a densité énergétique en 1 ($e_1$) et a densité énergétique en 2 ($e_2$) doivent tre gaux :
Ceci n'est possible que si la viscosit est n gligeable, car elle est associ e la diffusion d' nergie, et qu'il n'y a pas de tourbillons pr sents, lesquels pr sentent eux-m mes des diff rences d' nergie dues aux vitesses tangentes variables le long du rayon du vortex.
tant donn qu'un fluide ou un gaz est un continuum, le concept d' nergie ne peut plus tre associ une masse sp cifique. Cependant, il est possible de consid rer l' nergie contenue dans un volume du continuum, et en la divisant par le volume lui-m me, nous obtenons a densité d'énergie ($e$). Par cons quent, avec a densité ($\rho$), a vitesse dans un rayon du cylindre ($v$), a hauteur de la colonne ($h$), a accélération gravitationnelle ($g$) et a pression de la colonne d'eau ($p$), nous avons :
qui correspond l' quation de Bernoulli.
tant donn qu'un fluide ou un gaz est un continuum, le concept d' nergie ne peut plus tre associ une masse sp cifique. Cependant, il est possible de consid rer l' nergie contenue dans un volume du continuum, et en la divisant par le volume lui-m me, nous obtenons a densité d'énergie ($e$). Par cons quent, avec a densité ($\rho$), a vitesse dans un rayon du cylindre ($v$), a hauteur de la colonne ($h$), a accélération gravitationnelle ($g$) et a pression de la colonne d'eau ($p$), nous avons :
qui correspond l' quation de Bernoulli.
Avec a vitesse moyenne du fluide au point 1 ($v_1$), a hauteur ou profondeur 1 ($h_1$) et a pression dans la colonne 1 ($p_1$) repr sentant la vitesse, la hauteur et la pression au point 1, respectivement, et a vitesse moyenne du fluide au point 2 ($v_2$), a hauteur ou profondeur 2 ($h_2$) et a pression dans la colonne 2 ($p_2$) repr sentant la vitesse, la hauteur et la pression au point 2, respectivement, nous avons :
La diff rence de hauteur, repr sent e par a différence de hauteur ($\Delta h$), implique que la pression dans les deux colonnes est diff rente. En particulier, a différence de pression ($\Delta p$) est une fonction de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), et a différence de hauteur ($\Delta h$), comme suit :
Lorsque deux colonnes de liquide sont connect es avec a hauteur de colonne de liquide 1 ($h_1$) et a hauteur de colonne de liquide 2 ($h_2$), une a différence de hauteur ($\Delta h$) est form e, qui est calcul e comme suit :
a différence de hauteur ($\Delta h$) g n rera la diff rence de pression qui fera s' couler le liquide de la colonne la plus lev e vers la colonne la plus basse.
Lorsque deux colonnes de liquide sont connect es avec a pression dans la colonne 1 ($p_1$) et a pression dans la colonne 2 ($p_2$), une a différence de pression ($\Delta p$) est cr e, qui est calcul e selon la formule suivante :
a différence de pression ($\Delta p$) repr sente la diff rence de pression qui fera s' couler le liquide de la colonne la plus haute vers la colonne la plus basse.
A différence de vitesse entre les surfaces ($\Delta v$) est avec a vitesse moyenne du fluide au point 1 ($v_1$) et a vitesse moyenne du fluide au point 2 ($v_2$) est
ID:(684, 0)