Bernoulli sem pressão hidrostática
Storyboard 
No caso em que o fluxo ocorre em um gás ou em uma situação onde as variações de altura são mínimas, o efeito da pressão hidrostática pode ser negligenciado.
Sem a pressão hidrostática, a lei de Bernoulli reduz-se à soma de um termo associado à energia cinética, e assim à velocidade ao quadrado, e à pressão existente em cada local, mantendo-se constante. Isso implica que, se a velocidade aumenta, a pressão diminui, e vice-versa.
ID:(2066, 0)
Bernoulli sem pressão hidrostática
Storyboard 
No caso em que o fluxo ocorre em um gás ou em uma situação onde as variações de altura são mínimas, o efeito da pressão hidrostática pode ser negligenciado. Sem a pressão hidrostática, a lei de Bernoulli reduz-se à soma de um termo associado à energia cinética, e assim à velocidade ao quadrado, e à pressão existente em cada local, mantendo-se constante. Isso implica que, se a velocidade aumenta, a pressão diminui, e vice-versa.
Variáveis
Cálculos
Cálculos
Equações
No caso em que n o h press o hisstrost tica, aplica-se a lei de Bernoulli para la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la velocidade média do fluido no ponto 1 ($v_1$) e < var>5416
pode ser reescrito com ERROR:6673
e tendo em mente que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
com
e
se tem que
Outra equa o til aquela que corresponde conserva o de energia, a qual aplic vel em casos em que a viscosidade, um processo que resulta em perda de energia, pode ser negligenciada. Se considerarmos a equa o cl ssica da energia $E$, que leva em conta a energia cin tica, a energia potencial gravitacional e uma for a externa que desloca o l quido por uma dist ncia $\Delta z$, podemos express -la da seguinte forma:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Se considerarmos a energia em um volume $\Delta x\Delta y\Delta z$, podemos substituir a massa por:
$m=\rho \Delta x\Delta y\Delta z$
E como a press o dada por:
$F=p \Delta S =p \Delta y\Delta z$
Obtemos a equa o para a densidade de energia:
Outra equa o til aquela que corresponde conserva o de energia, a qual aplic vel em casos em que a viscosidade, um processo que resulta em perda de energia, pode ser negligenciada. Se considerarmos a equa o cl ssica da energia $E$, que leva em conta a energia cin tica, a energia potencial gravitacional e uma for a externa que desloca o l quido por uma dist ncia $\Delta z$, podemos express -la da seguinte forma:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Se considerarmos a energia em um volume $\Delta x\Delta y\Delta z$, podemos substituir a massa por:
$m=\rho \Delta x\Delta y\Delta z$
E como a press o dada por:
$F=p \Delta S =p \Delta y\Delta z$
Obtemos a equa o para a densidade de energia:
Exemplos
Se a energia conservada e o meio flui sem deforma o, segue que a densidade entre dois pontos deve ser igual, o que a premissa que leva lei de Bernoulli.
No caso da lei de Bernoulli [1], no caso em que n o existe press o hidrost tica, temos la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), < var>5415 e la velocidade média do fluido no ponto 2 ($v_2$):
A equa o de Bernoulli pressup e a conserva o da densidade de energia, o que implica na aus ncia de viscosidade e turbul ncia, tornando sua aplica o neste caso limitada.
A equa o de Bernoulli pode servir como base para modelar o processo, mas deve ser necessariamente complementada com um modelo que considere a possibilidade de incluir os efeitos da turbul ncia.
![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
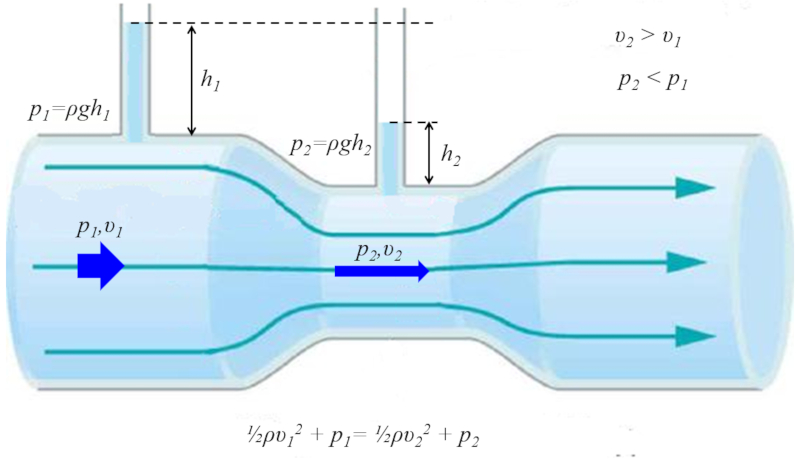
O tubo de Venturi apresenta uma se o mais estreita e dois tubos verticais para medir a press o. Quando o l quido circula pelo tubo, observa-se que as colunas na parte de maior se o s o mais altas, enquanto na parte de menor se o, a coluna mais baixa. Isso implica que na se o mais estreita, a velocidade do l quido maior, gerando uma menor press o din mica.
A situa o pode ser analisada e calculada usando a equa o geral de Bernoulli. Neste modelo, la velocidade média do fluido no ponto 1 ($v_1$) e la pressão na coluna 1 ($p_1$) correspondem velocidade, altura e press o no ponto 1, respectivamente. Da mesma forma, la velocidade média do fluido no ponto 2 ($v_2$) e la pressão na coluna 2 ($p_2$) representam a velocidade, altura e press o no ponto 2. A rela o expressa da seguinte maneira:
Tubos verticais permitem medir a press o em cada se o, pois a altura em que o l quido emerge corresponder press o hidrost tica naquela se o espec fica. Com la aceleração gravitacional ($g$), isso ser medido no primeiro ponto com la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$):
e no segundo ponto com la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$):
No caso em que n o h press o hisstrost tica, aplica-se a lei de Bernoulli para la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la velocidade média do fluido no ponto 1 ($v_1$) e < var>5416
pode ser reescrito com ERROR:6673
e tendo em mente que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
com
e
se tem que
Quando um carro ultrapassa outro na estrada, cria-se uma situa o em que um fluxo de ar de maior velocidade gerado entre os dois ve culos, resultando em uma press o mais baixa nessa rea. Como resultado, a press o nas laterais externas dos carros faz com que eles se atraiam mutuamente.
medida que os ve culos se cruzam, a velocidade relativa entre eles diminui e se aproxima do repouso, gerando uma press o mais alta entre eles e fazendo com que se afastem um do outro.
O mesmo fen meno ocorre quando dois barcos se cruzam. Se o cruzamento ocorrer em um canal estreito, ambos os timoneiros devem direcionar seus navios para o lado oposto para evitar que a for a repulsiva cause uma colis o com a borda do canal.
Para explicar por que isso acontece, podemos aplicar a equa o ERROR:6673 com la velocidade média ($\bar{v}$) e la diferença de velocidade entre superfícies ($\Delta v$) com la densidade ($\rho$) usando
Portanto, pode-se observar que se houver um gradiente de velocidade, ele inversamente proporcional ao gradiente de press o. Se um aumenta, o outro diminui, explicando por que os carros ultrapassados apresentam uma velocidade mais alta entre eles, levando a uma redu o na press o entre eles, causando suc o m tua. Por outro lado, se eles se cruzam, a velocidade entre eles aproximadamente zero, gerando um gradiente de press o que os afasta.
Neste caso, pode-se assumir que la velocidade média do fluido no ponto 2 ($v_2$) representa uma velocidade nula e la velocidade média do fluido no ponto 1 ($v_1$) corresponde a la velocidade de fluxo ($v_s$). Portanto, para la diferença de velocidade entre superfícies ($\Delta v$) estabelece-se o seguinte:
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
e para la velocidade média ($\bar{v}$) calcula-se:
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$
Consequentemente, com ERROR:6673, que igual a la diferença de pressão ($\Delta p_s$), obtemos:
resultando em:
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
o que leva a:
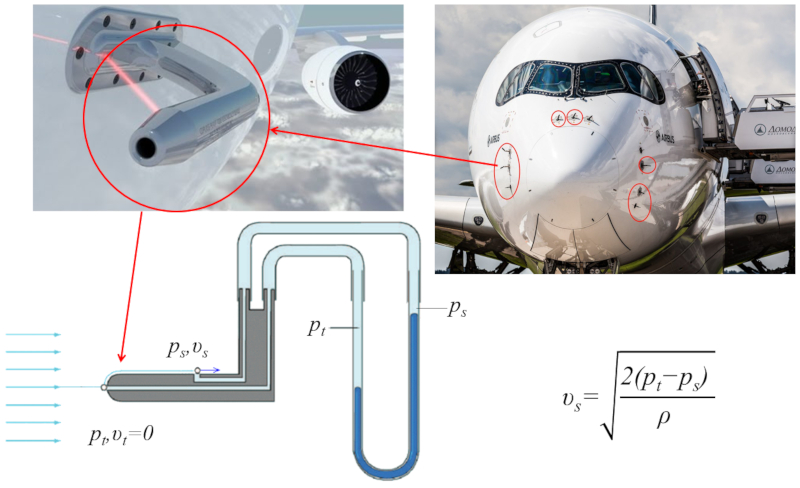
A velocidade de uma aeronave determinada usando um dispositivo chamado tubo de Pitot. Ele consiste em duas aberturas: uma na frente (borda de ataque) e outra em um dos lados. Na borda de ataque, a velocidade nula, enquanto na abertura lateral, registrada a velocidade com que a aeronave avan a em rela o ao ar circundante. Nas aberturas do tubo, h dois tubos preenchidos com um l quido para medir a diferen a de press o entre os dois pontos. Utilizando a equa o de Bernoulli, poss vel calcular a velocidade da aeronave a partir da diferen a de press o e da densidade do l quido.
Em particular, a velocidade na ponta do tubo de Pitot nula, o que reduz la diferença de velocidade entre superfícies ($\Delta v$) velocidade no orif cio lateral ($\Delta v = v$), enquanto la velocidade média ($\bar{v}$) equivale metade dessa velocidade ($\bar{v} = v/2$). Uma vez que la velocidade de fluxo ($v_s$) representa a velocidade do avi o, esta pode ser determinada medindo la diferença de pressão ($\Delta p_s$) utilizando a seguinte equa o:
importante notar que esta equa o requer a densidade, que varia com a altitude em que a aeronave est voando.
Se a energia for conservada dentro dos volumes que fluem com o fluxo, ent o la densidade de energia em 1 ($e_1$) e la densidade de energia em 2 ($e_2$) devem ser iguais:
Isso s poss vel se a viscosidade for negligenci vel, pois ela est associada difus o de energia, e n o h v rtices presentes, os quais apresentam diferen as de energia devido s velocidades tangenciais variadas ao longo do raio do v rtice.
Uma vez que um fluido ou g s um cont nuo, o conceito de energia j n o pode ser associado a uma massa espec fica. No entanto, poss vel considerar a energia contida num volume do cont nuo e, ao dividir pela pr pria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade média do fluido ($v$) e la pressão da coluna de água ($p$), temos:
o que corresponde equa o de Bernoulli.
Na aus ncia de viscosidade, a conserva o de energia implica que la densidade de energia ($e$) seja constante em qualquer ponto do fluido. Portanto, conhecer a velocidade e/ou a press o em qualquer local do fluido suficiente para estabelecer uma rela o entre a velocidade e a press o em qualquer ponto do fluido.
Uma vez que um fluido ou g s um cont nuo, o conceito de energia j n o pode ser associado a uma massa espec fica. No entanto, poss vel considerar a energia contida num volume do cont nuo e, ao dividir pela pr pria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade média do fluido ($v$) e la pressão da coluna de água ($p$), temos:
o que corresponde equa o de Bernoulli.
Na aus ncia de viscosidade, a conserva o de energia implica que la densidade de energia ($e$) seja constante em qualquer ponto do fluido. Portanto, conhecer a velocidade e/ou a press o em qualquer local do fluido suficiente para estabelecer uma rela o entre a velocidade e a press o em qualquer ponto do fluido.
No caso da lei de Bernoulli, no caso em que n o existe press o hidrost tica, temos la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), < var>5415 e la velocidade média do fluido no ponto 2 ($v_2$):
Quando duas colunas de l quido s o conectadas com la pressão na coluna 1 ($p_1$) e la pressão na coluna 2 ($p_2$), criada uma la diferença de pressão ($\Delta p$) que calculada de acordo com a seguinte f rmula:
la diferença de pressão ($\Delta p$) representa a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.
La velocidade média ($\bar{v}$) est com la velocidade média do fluido no ponto 1 ($v_1$) e la velocidade média do fluido no ponto 2 ($v_2$)
La diferença de velocidade entre superfícies ($\Delta v$) est com la velocidade média do fluido no ponto 1 ($v_1$) e la velocidade média do fluido no ponto 2 ($v_2$)
ERROR:6673 pode ser calculado a partir de la velocidade média ($\bar{v}$) e la diferença de velocidade entre superfícies ($\Delta v$) com la densidade ($\rho$) usando
o que nos permite ver o efeito da velocidade m dia de um corpo e a diferen a entre suas superf cies, como observado na asa de um avi o ou de um p ssaro.
ID:(2066, 0)