Bernoulli sans pression hydrostatique
Storyboard 
Dans le cas où l'écoulement se produit dans un gaz ou dans une situation où les variations de hauteur sont minimes, l'effet de la pression hydrostatique peut être négligé.
Sans pression hydrostatique, la loi de Bernoulli se réduit à la somme d'un terme associé à l'énergie cinétique, et donc à la vitesse au carré, et la pression existante à chaque emplacement reste constante. Cela signifie que si la vitesse augmente, la pression diminue, et vice versa.
ID:(2066, 0)
Bernoulli sans pression hydrostatique
Storyboard 
Dans le cas où l'écoulement se produit dans un gaz ou dans une situation où les variations de hauteur sont minimes, l'effet de la pression hydrostatique peut être négligé. Sans pression hydrostatique, la loi de Bernoulli se réduit à la somme d'un terme associé à l'énergie cinétique, et donc à la vitesse au carré, et la pression existante à chaque emplacement reste constante. Cela signifie que si la vitesse augmente, la pression diminue, et vice versa.
Variables
Calculs
Calculs
Équations
Dans le cas o il n'y a pas de pression hystrostatique, la loi de Bernoulli pour a densité ($\rho$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), a vitesse moyenne du fluide au point 1 ($v_1$) et < var>5416
peut tre r crit avec ERROR:6673
et en gardant l'esprit que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
avec
et
il faut que
Une autre quation utile est celle correspondant la conservation de l' nergie, qui s'applique dans les cas o la viscosit , un processus entra nant une perte d' nergie, peut tre n glig e. Si l'on consid re l' quation classique de l' nergie $E$, qui prend en compte l\' nergie cin tique, l\' nergie potentielle gravitationnelle et une force externe d pla ant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la mani re suivante :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si l\'on consid re l\' nergie l\'int rieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :
$m=\rho \Delta x\Delta y\Delta z$
Et puisque la pression est donn e par :
$F=p \Delta S =p \Delta y\Delta z$
On obtient l\' quation de la densit d\' nergie :
Une autre quation utile est celle correspondant la conservation de l' nergie, qui s'applique dans les cas o la viscosit , un processus entra nant une perte d' nergie, peut tre n glig e. Si l'on consid re l' quation classique de l' nergie $E$, qui prend en compte l\' nergie cin tique, l\' nergie potentielle gravitationnelle et une force externe d pla ant le liquide sur une distance $\Delta z$, on peut l\'exprimer de la mani re suivante :
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Si l\'on consid re l\' nergie l\'int rieur d\'un volume $\Delta x\Delta y\Delta z$, on peut remplacer la masse par :
$m=\rho \Delta x\Delta y\Delta z$
Et puisque la pression est donn e par :
$F=p \Delta S =p \Delta y\Delta z$
On obtient l\' quation de la densit d\' nergie :
Exemples
Si l' nergie est conserv e et que le milieu s' coule sans se d former, il s'ensuit que la densit entre deux points doit tre gale, ce qui est la pr misse conduisant la loi de Bernoulli.
Dans le cas de la loi de Bernoulli [1], dans le cas o il n'y a pas de pression hydrostatique, on a a densité ($\rho$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), < var>5415 et a vitesse moyenne du fluide au point 2 ($v_2$) :
L' quation de Bernoulli suppose la conservation de la densit d' nergie, ce qui implique l'absence de viscosit et de turbulence, limitant ainsi son application dans ce cas.
L' quation de Bernoulli peut servir de base pour mod liser le processus, mais elle doit n cessairement tre compl t e par un mod le prenant en compte la possibilit d'inclure les effets de la turbulence.
![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
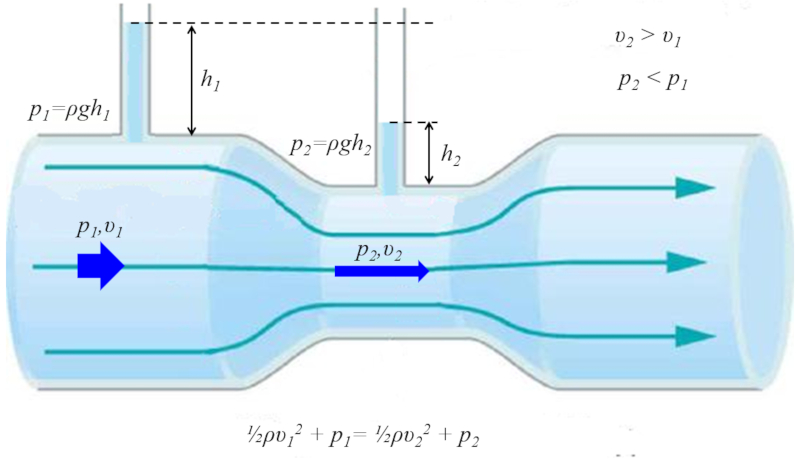
Le tube de Venturi est compos d'une section plus troite et de deux tubes verticaux pour mesurer la pression. Lorsque le liquide circule travers le tube, on observe que les colonnes dans la section plus large sont plus hautes, tandis que dans la section plus troite, la colonne est plus basse. Cela implique que dans la section plus troite, la vitesse du liquide est plus lev e, ce qui g n re une pression dynamique plus faible.
La situation peut tre analys e et calcul e en utilisant l' quation g n rale de Bernoulli. Dans ce mod le, a vitesse moyenne du fluide au point 1 ($v_1$) et a pression dans la colonne 1 ($p_1$) correspondent respectivement la vitesse, la hauteur et la pression au point 1. De m me, a vitesse moyenne du fluide au point 2 ($v_2$) et a pression dans la colonne 2 ($p_2$) repr sentent la vitesse, la hauteur et la pression au point 2. La relation est exprim e de la mani re suivante :
Les tubes verticaux permettent de mesurer la pression dans chaque section, car la hauteur laquelle le liquide merge correspondra la pression hydrostatique dans cette section sp cifique. Avec a accélération gravitationnelle ($g$), cela sera mesur au premier point avec a hauteur ou profondeur 1 ($h_1$) et a pression dans la colonne 1 ($p_1$) :
et au deuxi me point avec a hauteur ou profondeur 2 ($h_2$) et a pression dans la colonne 2 ($p_2$) :
Dans le cas o il n'y a pas de pression hystrostatique, la loi de Bernoulli pour a densité ($\rho$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), a vitesse moyenne du fluide au point 1 ($v_1$) et < var>5416
peut tre r crit avec ERROR:6673
et en gardant l'esprit que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
avec
et
il faut que
Lorsqu'une voiture d passe une autre sur la route, cela cr e une situation o un flux d'air plus rapide est g n r entre les deux v hicules, entra nant une pression plus basse dans cette zone. En cons quence, la pression sur les c t s ext rieurs des voitures les attire mutuellement.
Lorsque les v hicules se croisent, la vitesse relative entre eux diminue et se rapproche du repos, g n rant une pression plus lev e entre eux et les loignant l'un de l'autre.
Le m me ph nom ne se produit lorsque deux bateaux se croisent. Si le croisement se fait dans un canal troit, les deux barreurs doivent diriger leurs navires vers le c t oppos pour viter que la force r pulsive ne provoque une collision avec le bord du canal.
Pour expliquer pourquoi cela se produit, nous pouvons appliquer l' quation ERROR:6673 avec a vitesse moyenne ($\bar{v}$) et a différence de vitesse entre les surfaces ($\Delta v$) avec a densité ($\rho$) en utilisant
Il est donc possible de constater que s'il y a un gradient de vitesse, il est inversement proportionnel au gradient de pression. Si l'un augmente, l'autre diminue, ce qui explique pourquoi les voitures d pass es pr sentent une vitesse plus lev e entre elles, entra nant une r duction de la pression entre elles et provoquant une aspiration mutuelle. En revanche, s'ils se croisent, la vitesse entre eux est approximativement nulle, g n rant un gradient de pression qui les repousse.
Dans ce cas, il peut tre assum que a vitesse moyenne du fluide au point 2 ($v_2$) repr sente une vitesse nulle et a vitesse moyenne du fluide au point 1 ($v_1$) correspond a vitesse d'écoulement ($v_s$). Ainsi, pour a différence de vitesse entre les surfaces ($\Delta v$), il est tabli que :
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
et pour a vitesse moyenne ($\bar{v}$), on calcule :
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$
En cons quence, avec ERROR:6673, qui est gal a différence de pression ($\Delta p_s$), on obtient :
ce qui r sulte en :
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
ce qui conduit :
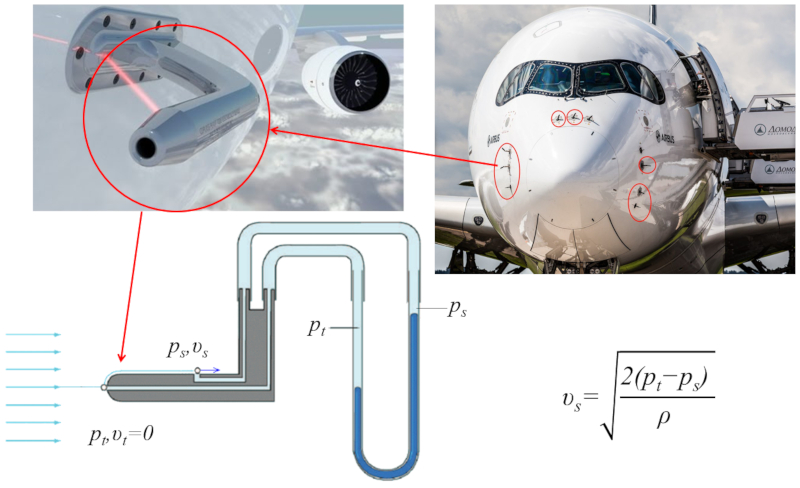
La vitesse d'un avion est d termin e l'aide d'un dispositif appel tube de Pitot. Il se compose de deux ouvertures : une l'avant (bord d\'attaque) et une sur le c t . Au niveau du bord d\'attaque, la vitesse est nulle, tandis qu\' l\'ouverture lat rale, elle repr sente la vitesse laquelle l\'avion se d place par rapport l\'air environnant. l\'int rieur des ouvertures, il y a deux tubes remplis de liquide, permettant de mesurer la diff rence de pression entre les deux points. En utilisant l\' quation de Bernoulli, il est possible de calculer la vitesse de l\'avion partir de la diff rence de pression et de la densit du liquide.
En particulier, la vitesse la pointe du tube de Pitot est nulle, ce qui r duit a différence de vitesse entre les surfaces ($\Delta v$) la vitesse au niveau de l'orifice lat ral ($\Delta v = v$), tandis que a vitesse moyenne ($\bar{v}$) correspond la moiti de cette vitesse ($\bar{v} = v/2$). tant donn que a vitesse d'écoulement ($v_s$) repr sente la vitesse de l'avion, celle-ci peut tre d termin e en mesurant a différence de pression ($\Delta p_s$) l'aide de l' quation suivante :
Il est important de noter que cette quation n cessite la densit , qui varie avec l'altitude laquelle l'avion vole.
Si l' nergie est conserv e au sein des volumes en coulement, alors a densité énergétique en 1 ($e_1$) et a densité énergétique en 2 ($e_2$) doivent tre gaux :
Ceci n'est possible que si la viscosit est n gligeable, car elle est associ e la diffusion d' nergie, et qu'il n'y a pas de tourbillons pr sents, lesquels pr sentent eux-m mes des diff rences d' nergie dues aux vitesses tangentes variables le long du rayon du vortex.
tant donn qu'un fluide ou un gaz est un continuum, le concept d' nergie ne peut plus tre associ une masse sp cifique. Cependant, il est possible de consid rer l' nergie contenue dans un volume du continuum, et en la divisant par le volume lui-m me, nous obtenons a densité d'énergie ($e$). Par cons quent, avec a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a pression de la colonne d'eau ($p$), nous avons :
qui correspond l' quation de Bernoulli.
En l'absence de viscosit , la conservation de l' nergie implique que a densité d'énergie ($e$) soit constant n'importe quel point du fluide. Par cons quent, conna tre la vitesse et/ou la pression en tout endroit du fluide est suffisant pour tablir une relation entre la vitesse et la pression en tout point du fluide.
tant donn qu'un fluide ou un gaz est un continuum, le concept d' nergie ne peut plus tre associ une masse sp cifique. Cependant, il est possible de consid rer l' nergie contenue dans un volume du continuum, et en la divisant par le volume lui-m me, nous obtenons a densité d'énergie ($e$). Par cons quent, avec a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a pression de la colonne d'eau ($p$), nous avons :
qui correspond l' quation de Bernoulli.
En l'absence de viscosit , la conservation de l' nergie implique que a densité d'énergie ($e$) soit constant n'importe quel point du fluide. Par cons quent, conna tre la vitesse et/ou la pression en tout endroit du fluide est suffisant pour tablir une relation entre la vitesse et la pression en tout point du fluide.
Dans le cas de la loi de Bernoulli, dans le cas o il n'y a pas de pression hydrostatique, on a a densité ($\rho$), a pression dans la colonne 1 ($p_1$), a pression dans la colonne 2 ($p_2$), < var>5415 et a vitesse moyenne du fluide au point 2 ($v_2$) :
Lorsque deux colonnes de liquide sont connect es avec a pression dans la colonne 1 ($p_1$) et a pression dans la colonne 2 ($p_2$), une a différence de pression ($\Delta p$) est cr e, qui est calcul e selon la formule suivante :
a différence de pression ($\Delta p$) repr sente la diff rence de pression qui fera s' couler le liquide de la colonne la plus haute vers la colonne la plus basse.
A vitesse moyenne ($\bar{v}$) est avec a vitesse moyenne du fluide au point 1 ($v_1$) et a vitesse moyenne du fluide au point 2 ($v_2$) est
A différence de vitesse entre les surfaces ($\Delta v$) est avec a vitesse moyenne du fluide au point 1 ($v_1$) et a vitesse moyenne du fluide au point 2 ($v_2$) est
ERROR:6673 peut tre calcul partir de a vitesse moyenne ($\bar{v}$) et a différence de vitesse entre les surfaces ($\Delta v$) avec a densité ($\rho$) en utilisant
ce qui nous permet de voir l'effet de la vitesse moyenne d'un corps et de la diff rence entre ses surfaces, comme observ dans une aile d'avion ou d'oiseau.
ID:(2066, 0)