Bernoulli without hydrostatic pressure
Storyboard 
In the case where flow occurs in a gas or in a situation where height variations are minimal, the effect of hydrostatic pressure can be neglected.
Without hydrostatic pressure, Bernoulli's law reduces to the sum of a term associated with kinetic energy, and thus with velocity squared, and the pressure existing at each location remaining constant. This implies that if velocity increases, pressure decreases, and vice versa.
ID:(2066, 0)
Bernoulli's law, without hydrostatic pressure
Image 
If energy is conserved and the medium flows without deforming, it follows that the density between two points must be equal, which is the premise leading to Bernoulli's law.
In the case of Bernoulli's law [1], in the case where there is no hydrostatic pressure, we have the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$):
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
The Bernoulli equation assumes the conservation of energy density, implying the absence of viscosity and turbulence, making its application in this case limited.
The Bernoulli equation can serve as a foundation for modeling the process, but it must necessarily be supplemented with a model that accounts for the possibility of including the effects of turbulence.
![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
ID:(15503, 0)
Venturi tube
Note 
The Venturi tube consists of a narrower section and two vertical tubes to measure pressure. When the fluid flows through the tube, it is observed that the columns in the larger section are taller, while in the narrower section, the column is shorter. This implies that in the narrower section, the velocity of the fluid is higher, resulting in lower dynamic pressure.
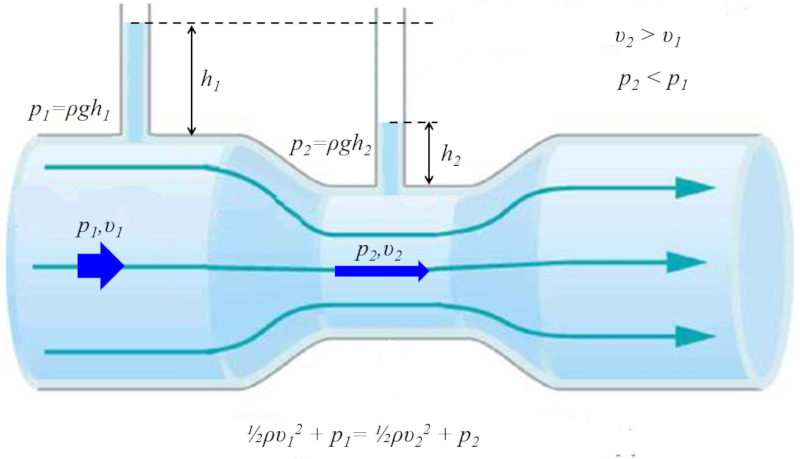
The situation can be analyzed and calculated using the general Bernoulli equation. In this model, the mean Speed of Fluid in Point 1 ($v_1$) and the pressure in column 1 ($p_1$) correspond to the velocity, height, and pressure at point 1, respectively. Similarly, the mean Speed of Fluid in Point 2 ($v_2$) and the pressure in column 2 ($p_2$) represent the velocity, height, and pressure at point 2. The relationship is expressed as follows:
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
Vertical tubes allow measuring the pressure in each section, as the height at which the liquid emerges will correspond to the hydrostatic pressure in that specific section. With the gravitational Acceleration ($g$), this will be measured at the first point with the height or depth 1 ($h_1$) and the pressure in column 1 ($p_1$):
| $ p = \rho_w g h $ |
and at the second point with the height or depth 2 ($h_2$) and the pressure in column 2 ($p_2$):
| $ p = \rho_w g h $ |
ID:(11093, 0)
Pressure difference
Quote 
In the case where there is no hystrostatic pressure, Bernoulli's law for the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$)
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
can be rewritten with the variación de la Presión ($\Delta p$)
| $ dp = p - p_0 $ |
and keeping in mind that
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
with
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
and
| $ \Delta v = v_2 - v_1 $ |
you have to
| $ \Delta p = - \rho \bar{v} \Delta v $ |
ID:(15709, 0)
Overpass and crossing of vehicles on the road
Exercise 
When overtaking a car on the road, a situation arises where a higher-speed airflow is generated between the two vehicles, resulting in lower pressure in that area. Consequently, the pressure on the outer sides of the cars causes them to attract each other.
As vehicles cross paths, the relative velocity between them decreases and approaches rest, generating higher pressure between them and causing them to move away from each other.

The same phenomenon occurs when two boats cross paths. If the crossing takes place in a narrow channel, both helmsmen must steer their vessels towards the opposite side to prevent the repulsive force from causing a collision with the channel's edge.
To explain why this happens, we can apply the equation the variación de la Presión ($\Delta p$) with the average speed ($\bar{v}$) and the speed difference between surfaces ($\Delta v$) with the density ($\rho$) using
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Therefore, it can be seen that if there is a velocity gradient, it is inversely proportional to the pressure gradient. If one increases, the other decreases, explaining why overtaking cars exhibit higher velocity between them, leading to a reduction in pressure between them, causing mutual suction. Conversely, if they cross, the velocity between them is approximately zero, generating a pressure gradient that pushes them apart.
ID:(11094, 0)
Speed with respect to rest
Equation 
In this case, it can be assumed that the mean Speed of Fluid in Point 2 ($v_2$) represents zero velocity and the mean Speed of Fluid in Point 1 ($v_1$) corresponds to the flow speed ($v_s$). Therefore, for the speed difference between surfaces ($\Delta v$) the following is established:
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
and for the average speed ($\bar{v}$) it is calculated:
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$
Consequently, with the variación de la Presión ($\Delta p$), which equals the pressure difference ($\Delta p_s$), we obtain:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
resulting in:
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
leading to:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
ID:(15711, 0)
Pitot tube
Script 
The speed of an aircraft is determined using a device called a Pitot tube. It consists of two openings: one at the front (known as the \\\"leading edge\\\") and the other on the side. At the leading edge, the velocity is zero, while at the side opening, it represents the speed at which the aircraft is moving relative to the surrounding air. Inside the openings, there are two tubes filled with fluid, allowing the measurement of the pressure difference between the two points. By applying Bernoulli's equation, it is possible to calculate the velocity of the aircraft using the pressure difference and the fluid density.
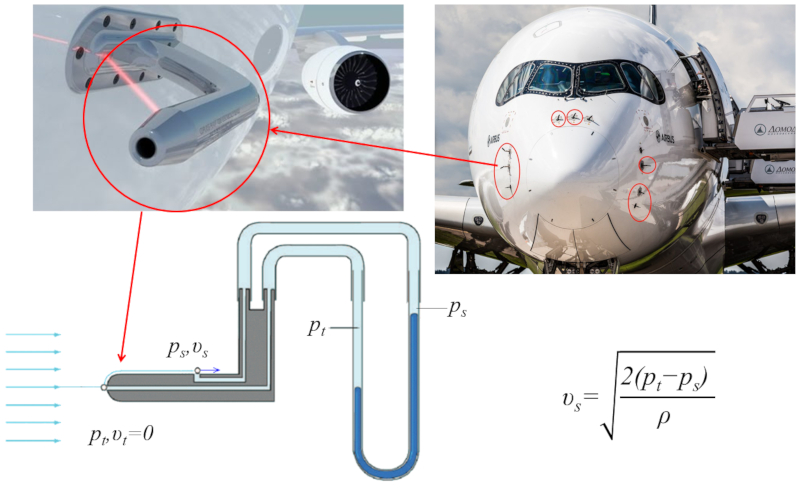
Specifically, the velocity at the tip of the Pitot tube is zero, which reduces the speed difference between surfaces ($\Delta v$) to the velocity at the side orifice ($\Delta v = v$), while the average speed ($\bar{v}$) equals half of that velocity ($\bar{v} = v/2$). Since the flow speed ($v_s$) represents the airplane's velocity, it can be determined by measuring the pressure difference ($\Delta p_s$) using the following equation:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
It's worth noting that this equation requires density, which varies with the altitude at which the aircraft is flying.
ID:(11095, 0)
Bernoulli without hydrostatic pressure
Description 
In the case where flow occurs in a gas or in a situation where height variations are minimal, the effect of hydrostatic pressure can be neglected. Without hydrostatic pressure, Bernoulli's law reduces to the sum of a term associated with kinetic energy, and thus with velocity squared, and the pressure existing at each location remaining constant. This implies that if velocity increases, pressure decreases, and vice versa.
Variables
Calculations
Calculations
Equations
(ID 4252)
In the case where there is no hystrostatic pressure, Bernoulli's law for the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$)
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
can be rewritten with the variación de la Presión ($\Delta p$)
| $ dp = p - p_0 $ |
and keeping in mind that
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
with
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
and
| $ \Delta v = v_2 - v_1 $ |
you have to
| $ \Delta p = - \rho \bar{v} \Delta v $ |
(ID 4835)
Another useful equation is the one corresponding to the conservation of energy, which is applicable in cases where viscosity, a process that leads to energy loss, can be neglected. If we consider the classic energy equation $E$, which takes into account kinetic energy, gravitational potential energy, and an external force displacing the liquid over a distance $\Delta z$, it can be expressed as:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
If we consider the energy within a volume $\Delta x\Delta y\Delta z$, we can replace the mass with:
$m=\rho \Delta x\Delta y\Delta z$
And since pressure is given by:
$F=p \Delta S =p \Delta y\Delta z$
We obtain the equation for energy density:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ p $ |
(ID 15496)
Another useful equation is the one corresponding to the conservation of energy, which is applicable in cases where viscosity, a process that leads to energy loss, can be neglected. If we consider the classic energy equation $E$, which takes into account kinetic energy, gravitational potential energy, and an external force displacing the liquid over a distance $\Delta z$, it can be expressed as:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
If we consider the energy within a volume $\Delta x\Delta y\Delta z$, we can replace the mass with:
$m=\rho \Delta x\Delta y\Delta z$
And since pressure is given by:
$F=p \Delta S =p \Delta y\Delta z$
We obtain the equation for energy density:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ p $ |
(ID 15496)
(ID 15499)
(ID 15502)
Examples
(ID 15497)
If energy is conserved and the medium flows without deforming, it follows that the density between two points must be equal, which is the premise leading to Bernoulli's law.
In the case of Bernoulli's law [1], in the case where there is no hydrostatic pressure, we have the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$):
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
The Bernoulli equation assumes the conservation of energy density, implying the absence of viscosity and turbulence, making its application in this case limited.
The Bernoulli equation can serve as a foundation for modeling the process, but it must necessarily be supplemented with a model that accounts for the possibility of including the effects of turbulence.
![]() [1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)
(ID 15503)
The Venturi tube consists of a narrower section and two vertical tubes to measure pressure. When the fluid flows through the tube, it is observed that the columns in the larger section are taller, while in the narrower section, the column is shorter. This implies that in the narrower section, the velocity of the fluid is higher, resulting in lower dynamic pressure.

The situation can be analyzed and calculated using the general Bernoulli equation. In this model, the mean Speed of Fluid in Point 1 ($v_1$) and the pressure in column 1 ($p_1$) correspond to the velocity, height, and pressure at point 1, respectively. Similarly, the mean Speed of Fluid in Point 2 ($v_2$) and the pressure in column 2 ($p_2$) represent the velocity, height, and pressure at point 2. The relationship is expressed as follows:
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
Vertical tubes allow measuring the pressure in each section, as the height at which the liquid emerges will correspond to the hydrostatic pressure in that specific section. With the gravitational Acceleration ($g$), this will be measured at the first point with the height or depth 1 ($h_1$) and the pressure in column 1 ($p_1$):
| $ p = \rho_w g h $ |
and at the second point with the height or depth 2 ($h_2$) and the pressure in column 2 ($p_2$):
| $ p = \rho_w g h $ |
(ID 11093)
In the case where there is no hystrostatic pressure, Bernoulli's law for the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$)
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
can be rewritten with the variación de la Presión ($\Delta p$)
| $ dp = p - p_0 $ |
and keeping in mind that
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
with
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
and
| $ \Delta v = v_2 - v_1 $ |
you have to
| $ \Delta p = - \rho \bar{v} \Delta v $ |
(ID 15709)
When overtaking a car on the road, a situation arises where a higher-speed airflow is generated between the two vehicles, resulting in lower pressure in that area. Consequently, the pressure on the outer sides of the cars causes them to attract each other.
As vehicles cross paths, the relative velocity between them decreases and approaches rest, generating higher pressure between them and causing them to move away from each other.

The same phenomenon occurs when two boats cross paths. If the crossing takes place in a narrow channel, both helmsmen must steer their vessels towards the opposite side to prevent the repulsive force from causing a collision with the channel's edge.
To explain why this happens, we can apply the equation the variación de la Presión ($\Delta p$) with the average speed ($\bar{v}$) and the speed difference between surfaces ($\Delta v$) with the density ($\rho$) using
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Therefore, it can be seen that if there is a velocity gradient, it is inversely proportional to the pressure gradient. If one increases, the other decreases, explaining why overtaking cars exhibit higher velocity between them, leading to a reduction in pressure between them, causing mutual suction. Conversely, if they cross, the velocity between them is approximately zero, generating a pressure gradient that pushes them apart.
(ID 11094)
In this case, it can be assumed that the mean Speed of Fluid in Point 2 ($v_2$) represents zero velocity and the mean Speed of Fluid in Point 1 ($v_1$) corresponds to the flow speed ($v_s$). Therefore, for the speed difference between surfaces ($\Delta v$) the following is established:
$\Delta v = v_2 - v_1 = 0 - v_s = - v_s$
and for the average speed ($\bar{v}$) it is calculated:
$\bar{v} = \displaystyle\frac{v_1 + v_2}{2} = \frac{v_s}{2}$
Consequently, with the variación de la Presión ($\Delta p$), which equals the pressure difference ($\Delta p_s$), we obtain:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
resulting in:
$\Delta p_s = \displaystyle\frac{1}{2} \rho v_s^2$
leading to:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
(ID 15711)
The speed of an aircraft is determined using a device called a Pitot tube. It consists of two openings: one at the front (known as the \\\"leading edge\\\") and the other on the side. At the leading edge, the velocity is zero, while at the side opening, it represents the speed at which the aircraft is moving relative to the surrounding air. Inside the openings, there are two tubes filled with fluid, allowing the measurement of the pressure difference between the two points. By applying Bernoulli's equation, it is possible to calculate the velocity of the aircraft using the pressure difference and the fluid density.

Specifically, the velocity at the tip of the Pitot tube is zero, which reduces the speed difference between surfaces ($\Delta v$) to the velocity at the side orifice ($\Delta v = v$), while the average speed ($\bar{v}$) equals half of that velocity ($\bar{v} = v/2$). Since the flow speed ($v_s$) represents the airplane's velocity, it can be determined by measuring the pressure difference ($\Delta p_s$) using the following equation:
| $ v_s = \sqrt{\displaystyle\frac{2 \Delta p_s }{ \rho }}$ |
It's worth noting that this equation requires density, which varies with the altitude at which the aircraft is flying.
(ID 11095)
(ID 15498)
If energy is conserved within the flowing volumes, then the energy density in 1 ($e_1$) and the energy density in 2 ($e_2$) must be equal:
| $ e_1 = e_2 $ |
This is only possible if viscosity is negligible, as it is associated with energy diffusion, and there are no vortices present, which themselves exhibit energy differences due to varying tangential velocities along the vortex radius.
(ID 15499)
Since a fluid or gas is a continuum, the concept of energy can no longer be associated with a specific mass. However, it is possible to consider the energy contained in a volume of the continuum, and by dividing it by the volume itself, we obtain the energy density ($e$). Therefore, with the density ($\rho$), the mean Speed of Fluid ($v$) and the water column pressure ($p$), we have:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ p $ |
which corresponds to the Bernoulli equation.
In the absence of viscosity, the conservation of energy implies that the energy density ($e$) is constant at any point in the fluid. Therefore, knowing the velocity and/or pressure at any location in the fluid is sufficient to establish a relationship between velocity and pressure at any point in the fluid.
(ID 15496)
Since a fluid or gas is a continuum, the concept of energy can no longer be associated with a specific mass. However, it is possible to consider the energy contained in a volume of the continuum, and by dividing it by the volume itself, we obtain the energy density ($e$). Therefore, with the density ($\rho$), the mean Speed of Fluid ($v$) and the water column pressure ($p$), we have:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ p $ |
which corresponds to the Bernoulli equation.
In the absence of viscosity, the conservation of energy implies that the energy density ($e$) is constant at any point in the fluid. Therefore, knowing the velocity and/or pressure at any location in the fluid is sufficient to establish a relationship between velocity and pressure at any point in the fluid.
(ID 15496)
In the case of Bernoulli's law, in the case where there is no hydrostatic pressure, we have the density ($\rho$), the pressure in column 1 ($p_1$), the pressure in column 2 ($p_2$), the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$):
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
(ID 15495)
When two liquid columns are connected with the pressure in column 1 ($p_1$) and the pressure in column 2 ($p_2$), a the pressure difference ($\Delta p$) is formed, which is calculated according to the following formula:
| $ dp = p - p_0 $ |
the pressure difference ($\Delta p$) represents the pressure difference that will cause the liquid to flow from the taller column to the shorter one.
(ID 4252)
The average speed ($\bar{v}$) is with the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$) is
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
(ID 15501)
The speed difference between surfaces ($\Delta v$) is with the mean Speed of Fluid in Point 1 ($v_1$) and the mean Speed of Fluid in Point 2 ($v_2$) is
| $ \Delta v = v_2 - v_1 $ |
(ID 15502)
The variación de la Presión ($\Delta p$) can be calculated from the average speed ($\bar{v}$) and the speed difference between surfaces ($\Delta v$) with the density ($\rho$) using
| $ \Delta p = - \rho \bar{v} \Delta v $ |
which allows us to see the effect of the average speed of a body and the difference between its surfaces, as observed in an airplane or bird wing.
(ID 4835)
ID:(2066, 0)
