Beispiele für elektrische Potentiale
Storyboard
Mit den vorher berechneten Beispielen der elektrischen Felder werden die elektrischen Potentiale berechnet.
ID:(1562, 0)
Energie eines Teilchens
Gleichung
Los potenciales eléctricos corresponden a energía potencial por carga por lo que generan o reducen velocidad en función de como aumenta o reduce la energía potencial. Por ello la conservación de energía lleva a que con
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11596, 0)
Leiterkugel mit Ladung
Bild
In einer leitenden Kugel mit Ladungen sind diese auf der Oberfläche verteilt und damit ist das Feld im Inneren null. Draußen verhält es sich wie eine Punktladung, die sich in der Mitte der Kugel befindet:

ID:(11451, 0)
Berechnung der elektrischen Potential, Punktladung
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_p = -\displaystyle\int_r^{\infty} du\,E_p(u)$ |
con
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
o sea con
| $ \varphi_p = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
ID:(11576, 0)
Berechnung der elektrische Potential, mit sphärischer Geometrie, außen
Gleichung
Como la diferencia de potencial con es igual
| $ \varphi_f = -\displaystyle\int_r^{\infty} du\,E_f(u)$ |
con
| $ E_f =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}\theta( r - R )$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_f = -\displaystyle\int_{\infty}^{r} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
o sea con
| $ \varphi_f = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
ID:(11582, 0)
Isolierkugel mit homogener Ladung
Bild
Eine isolierende Kugel, in der Ladungen homogen verteilt wurden und die nicht bewegt werden kann, weil es sich um ein isolierendes Material handelt, hat ein elektrisches Feld, das im Inneren linear wächst und mit der Umkehrung des quadratischen Radius abnimmt:

ID:(11450, 0)
Elektrisches Potential mit sphärischer Geometrie, isolierend, intern
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_i = -\displaystyle\int_0^r du\,E_i(u)$ |
con
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_i }{ R ^3 }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
o sea con
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }\theta( R - r ) $ |
ID:(11583, 0)
Elektrisches Potential mit sphärischer Geometrie, isolierend, aussen
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_e = - \displaystyle\int_0^R du\,E_i(u) - \displaystyle\int_R^r du\,E_e(u)$ |
con
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
y con
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_i }{ R ^3 }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
o sea con
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
ID:(11584, 0)
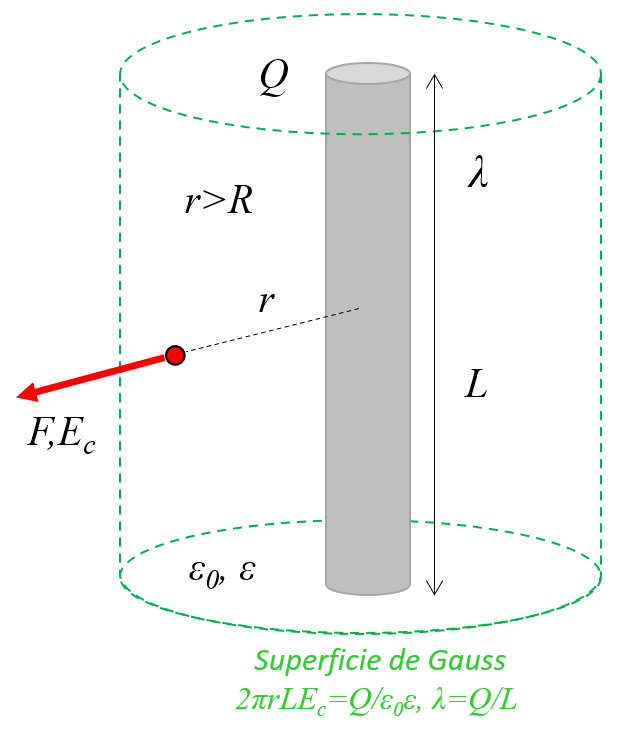
Geladener unendlicher Draht oder Zylinder im Vakuum
Bild
In einem Leiterdraht oder Zylinder mit Ladungen sind diese über das Objekt verteilt und verhalten sich wie eine lange Kette von Punktlasten, die auf der Achse ausgerichtet sind:
ID:(11452, 0)
Berechnung elektrischer Potentiale, zylindrischen Geometrie
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_c = -\displaystyle\int_{r_0}^r du\,E_c(u)$ |
con
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }\theta( r - R )$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_c = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln r$
o sea con
| $ \varphi_c = -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon }\ln r $ |
ID:(11585, 0)
Unendliche Leiterebene mit Last
Bild
In einer leitenden Ebene kann eine Gaußsche Oberfläche als Zylinder definiert werden. Die Seitenwände sind orthogonal zum Feld, so dass der einzige Teil, der dazu beiträgt, die Oberflächen parallel zur Ebene sind:

ID:(11453, 0)
Berechnung der elektrische Potential, Oberflächen
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_{s,d} = -\displaystyle\int_0^z du\,E_{s,d}(u)$ |
con
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
o sea con
| $ \varphi_s = -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z $ |
ID:(11586, 0)
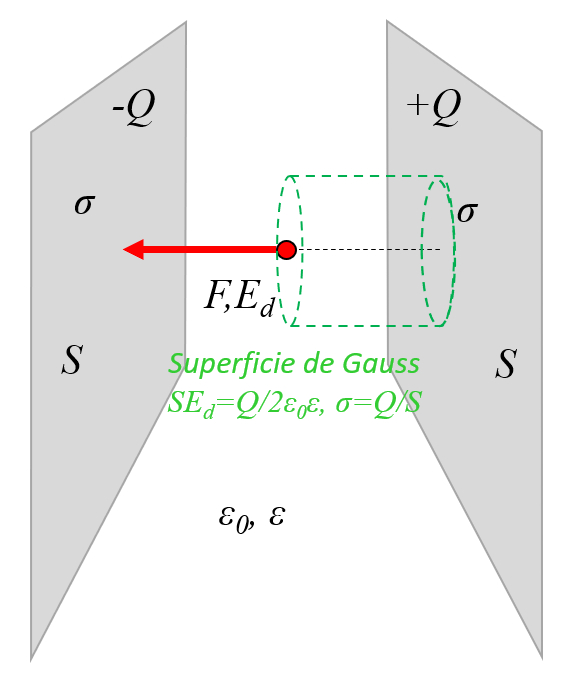
Einfaches Modell für zwei Platten mit entgegengesetzten Ladungen
Bild
Um das Feld zwischen den beiden Platten auf einfache Weise berechnen zu können, kann davon ausgegangen werden, dass das externe Feld kompensiert wird und dass sich das meiste nur zwischen den Platten befindet:
ID:(11455, 0)
Berechnung der elektrische Potential, Doppelplatten
Gleichung
Como la diferencia de potencial es con igual
| $ \varphi_{s,d} = -\displaystyle\int_0^z du\,E_{s,d}(u)$ |
con
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
o sea con
| $ \varphi_d = -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z $ |
ID:(11587, 0)
0
Video
Video: Beispiele für elektrische Potentiale
