Utilizador:
Flexão elástica
Storyboard 
Quando um torque é aplicado a um corpo, ele pode ser curvado ou flexionado. A forma como isso ocorre depende tanto da geometria do corpo quanto da maneira como o torque é aplicado. Além disso, é possível estimar a energia elástica absorvida pelo corpo com base na deformação que ele sofre.
ID:(2062, 0)
Flexão elástica
Descrição
Quando um torque é aplicado a um corpo, ele pode ser curvado ou flexionado. A forma como isso ocorre depende tanto da geometria do corpo quanto da maneira como o torque é aplicado. Além disso, é possível estimar a energia elástica absorvida pelo corpo com base na deformação que ele sofre.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Se observarmos como la força vertical no eixo da viga ($Q_z$) varia em fun o de la carga por comprimento na viga ($q_z$) sobre um elemento de la posição ao longo da viga ($x$), temos:
$Q - qdx - (Q + dQ) = 0$
portanto:
$-qdx - dQ = 0$
o que nos leva a:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
A varia o de o binário na viga ($M_y$) ao longo de la posição ao longo da viga ($x$) da ordem do bra o do comprimento do elemento la posição ao longo da viga ($x$) multiplicado por la força vertical no eixo da viga ($Q_z$), portanto:
$-M - Qdx + (M + dM) = 0$
o que implica:
$-Qdx + dM = 0$
ou seja:
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
Como a derivada de o binário na viga ($M_y$) em rela o a la posição ao longo da viga ($x$) resulta em la força vertical no eixo da viga ($Q_z$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
e a derivada de la força vertical no eixo da viga ($Q_z$) igual a menos la carga por comprimento na viga ($q_z$):
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
a derivada da primeira nos leva a:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
Se observarmos como la força axial na viga ($N_x$) varia em fun o de la força axial longa na viga ($n$) sobre um elemento de la posição ao longo da viga ($x$), obtemos:
$N - ndx - (N + dN) = 0$
portanto:
$-ndx - dN = 0$
o que nos leva a:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
Com o binário na viga ($M_y$), la carga por comprimento na viga ($q_z$) e la posição ao longo da viga ($x$), estabelece-se a equa o do torque:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
que, juntamente com a equa o de deslocamento envolvendo o módulo de Elasticidade ($E$), o momento de inércia da secção ($I_b$) e o deslocamento z ($u_z$):
| $ M_y = - E I_b \displaystyle\frac{d^2 u_z }{d x ^2}$ |
nos leva a:
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
Exemplos
(ID 15570)
(ID 15884)
Em geral, o binário na viga ($M_y$) deve ser aplicado em ambos os extremos para gerar a flex o:
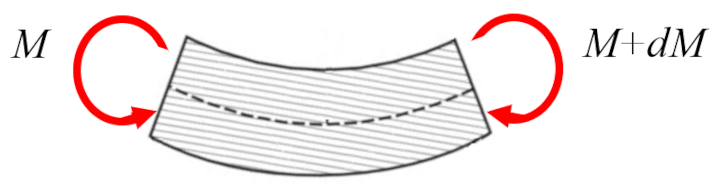
A diferen a entre ambos os torques igual ao torque gerado por la força vertical no eixo da viga ($Q_z$), com um intervalo correspondente varia o de la posição ao longo da viga ($x$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
Por sua vez, la força axial na viga ($N_x$) pode variar ao longo do eixo:
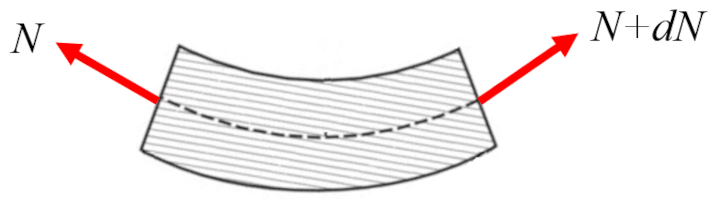
Essa varia o corresponde a la força axial longa na viga ($n$) ao longo do eixo:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
Finalmente, la força vertical no eixo da viga ($Q_z$) varia em fun o de la carga por comprimento na viga ($q_z$), o que pode corresponder ao peso pr prio da viga:
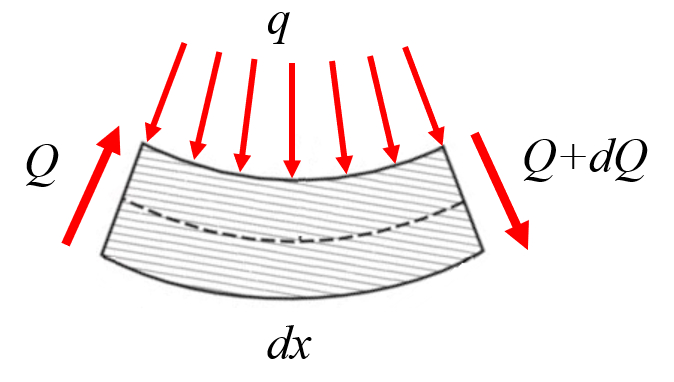
Assim, a varia o de la força vertical no eixo da viga ($Q_z$) ao longo de la posição ao longo da viga ($x$) corresponde a la carga por comprimento na viga ($q_z$) da seguinte forma:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
Ao combinar a primeira e a ltima equa o, obtemos a equa o de deforma o:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15885)
(ID 15886)
(ID 15887)
(ID 15571)
La carga por comprimento na viga ($q_z$) pode ser calculado com base em como la força vertical no eixo da viga ($Q_z$) varia ao longo de la posição ao longo da viga ($x$), portanto:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
La força axial longa na viga ($n$) pode ser calculado com base em como la força axial na viga ($N_x$) varia ao longo de la posição ao longo da viga ($x$), portanto:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
La força vertical no eixo da viga ($Q_z$) pode ser calculado com base em como o binário na viga ($M_y$) varia ao longo de la posição ao longo da viga ($x$), portanto:
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
A curvatura de o binário na viga ($M_y$) em la posição ao longo da viga ($x$) igual a menos la carga por comprimento na viga ($q_z$):
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
O momento de inércia da secção ($I_b$) de uma se o de uma barra calculado integrando sobre a se o no plano la posição em largura na viga ($y$) e la posição em altura na viga ($z$):
| $ I_b =\displaystyle\int dz dy z^2 $ |
(ID 15881)
(ID 14195)
Com a equa o de o binário na viga ($M_y$) em fun o de la carga por comprimento na viga ($q_z$) e la posição ao longo da viga ($x$), e a equa o para a flex o envolvendo o módulo de Elasticidade ($E$), o momento de inércia da secção ($I_b$) e o deslocamento z ($u_z$), temos que:
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
ID:(2062, 0)