Elastic flexion
Storyboard 
When a torque is applied to a body, it can be bent or flexed. The way this happens depends on both the geometry of the body and how the torque is applied. Additionally, it is possible to estimate the elastic energy absorbed by the body based on the deformation it undergoes.
ID:(2062, 0)
Bending a beam
Definition 
If a beam is bent, it is observed that the sections rotate by an angle

for which it is required to tension using shear (a pair of opposite tensions).
ID:(14185, 0)
Elastic flexion
Description 
When a torque is applied to a body, it can be bent or flexed. The way this happens depends on both the geometry of the body and how the torque is applied. Additionally, it is possible to estimate the elastic energy absorbed by the body based on the deformation it undergoes.
Variables
Calculations
Calculations
Equations
If we observe how the vertical force to the axis of the beam ($Q_z$) varies as a function of the load per length on the beam ($q_z$) over an element of the position along beam ($x$), we have:
$Q - qdx - (Q + dQ) = 0$
therefore:
$-qdx - dQ = 0$
which leads to:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
The variation of the torque on beam ($M_y$) along the position along beam ($x$) is of the order of the length of the arm of element the position along beam ($x$) multiplied by the vertical force to the axis of the beam ($Q_z$), therefore:
$-M - Qdx + (M + dM) = 0$
which implies:
$-Qdx + dM = 0$
in other words:
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
Since the torque on beam ($M_y$) derived with respect to the position along beam ($x$) gives the vertical force to the axis of the beam ($Q_z$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
and the derivative of the vertical force to the axis of the beam ($Q_z$) is equal to negative the load per length on the beam ($q_z$):
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
therefore, the derivative of the first leads us to:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
If we observe how the axial force on beam ($N_x$) varies as a function of the axial force along beam length ($n$) over an element of the position along beam ($x$), we get:
$N - ndx - (N + dN) = 0$
therefore:
$-ndx - dN = 0$
which leads us to:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
With the torque on beam ($M_y$), the load per length on the beam ($q_z$), and the position along beam ($x$), the torque equation is established:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
which, combined with the displacement equation involving the modulus of Elasticity ($E$), the moment of inertia of the section ($I_b$), and the displacement in z ($u_z$):
| $ M_y = - E I_b \displaystyle\frac{d^2 u_z }{d x ^2}$ |
results in:
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
Examples
(ID 15570)
(ID 15884)
In general, the torque on beam ($M_y$) must be applied to both ends to induce bending:
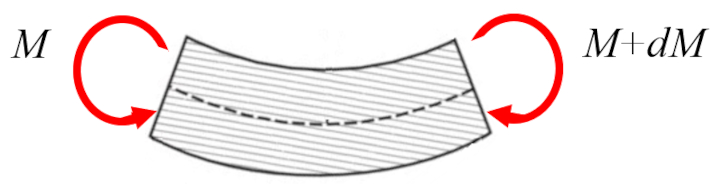
The difference between both torques is equal to the torque generated by the vertical force to the axis of the beam ($Q_z$), with an interval corresponding to the variation of the position along beam ($x$):
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
In turn, the axial force on beam ($N_x$) can vary along the axis:
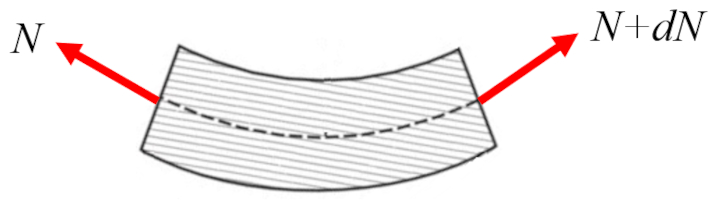
This variation corresponds to the axial force along beam length ($n$) along the axis:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
Finally, the vertical force to the axis of the beam ($Q_z$) varies as a function of the load per length on the beam ($q_z$), which may correspond to the beam's own weight:
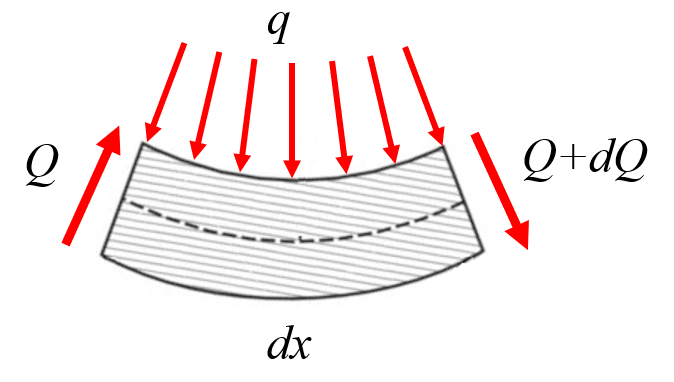
Thus, the variation of the vertical force to the axis of the beam ($Q_z$) along the position along beam ($x$) corresponds to the load per length on the beam ($q_z$) as follows:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
By combining the first and last equations, we obtain the deformation equation:
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15885)
(ID 15886)
(ID 15887)
(ID 15571)
The load per length on the beam ($q_z$) can be calculated based on how the vertical force to the axis of the beam ($Q_z$) varies along the position along beam ($x$), therefore:
| $\displaystyle\frac{d Q_z }{dx} = - q_z $ |
(ID 15888)
The axial force along beam length ($n$) can be calculated based on how the axial force on beam ($N_x$) varies along the position along beam ($x$), therefore:
| $\displaystyle\frac{d N_x }{d x } = - n $ |
(ID 15891)
The vertical force to the axis of the beam ($Q_z$) can be calculated based on how the torque on beam ($M_y$) varies along the position along beam ($x$), therefore:
| $\displaystyle\frac{d M_y }{d x } = Q_z $ |
(ID 15889)
The curvature of the torque on beam ($M_y$) in the position along beam ($x$) is equal to negative the load per length on the beam ($q_z$):
| $\displaystyle\frac{d^2 M_y }{d x ^2} = - q $ |
(ID 15890)
The moment of inertia of the section ($I_b$) for a section of a bar is calculated by integrating over the section in the plane the position within width of beam ($y$) and the position at height in beam ($z$):
| $ I_b =\displaystyle\int dz dy z^2 $ |
(ID 15881)
El momento de flexi n se calcula sumando todas las fuerzas que genera el s lido en la secci n multiplicado por la distancia de esta al eje en que rota la secci n. La suma de estos genera el momento de tensi n que tiene la forma
| $ M_y = - E I_b \displaystyle\frac{d^2 u_z }{d x ^2}$ |
(ID 14195)
With the equation for the torque on beam ($M_y$) as a function of the load per length on the beam ($q_z$) and the position along beam ($x$), and the equation for flexion involving the modulus of Elasticity ($E$), the moment of inertia of the section ($I_b$), and the displacement in z ($u_z$), we get:
| $ E I_b \displaystyle\frac{d^4 u_z }{d x ^4} = q_z $ |
(ID 15892)
ID:(2062, 0)
