Plastic deformation
Storyboard 
For small deformations, the material only undergoes elastic deformation, meaning that upon removing the load, it returns to its original shape. For larger deformations, atoms may experience greater displacements, leading to a permanent change in structure. In such cases, we refer to it as plastic deformation.
ID:(324, 0)
Plastic deformation
Storyboard 
For small deformations, the material only undergoes elastic deformation, meaning that upon removing the load, it returns to its original shape. For larger deformations, atoms may experience greater displacements, leading to a permanent change in structure. In such cases, we refer to it as plastic deformation.
Variables
Calculations
Calculations
Equations
Examples
The bone can be modeled as a hollow cylinder since the material inside it is not capable of bearing a significant load. Therefore, it is geometrically modeled as a cylinder with properties the body length ($L$), the inside radio ($R_1$), and the outdoor radio ($R_2$):
Therefore, the effective radius ($R$) is
the body Section ($S$) is
and the moment of inertia of surface ($I_s$) is
In the case of bone, there are different situations that lead to the generation of extreme tensions that result in fracture.
One situation is when the bone is fixed at one end and is being flexed from the other:
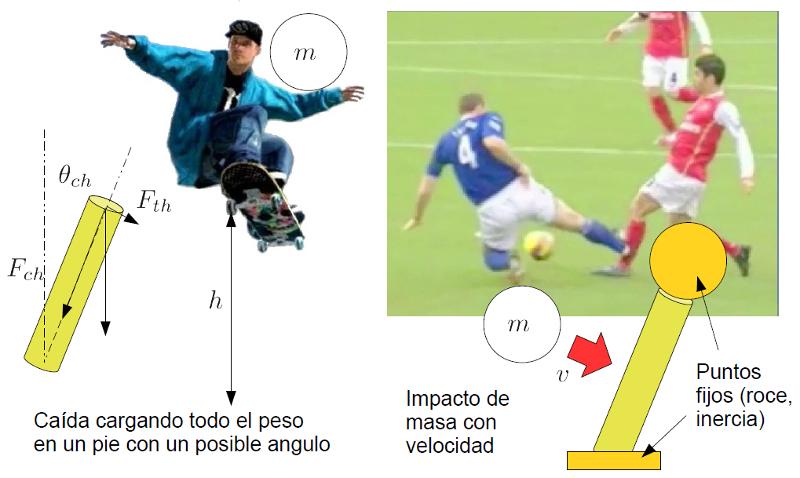
An example is a person falling and leaning on a point, creating a fixed point through friction while the center of mass continues to move due to inertia, flexing the bone until it fractures.
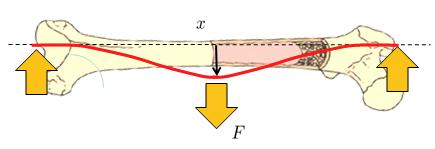
Another scenario is when it is fixed at both ends and receives a perpendicular force at some intermediate position:
A typical example of this is when a soccer player places their foot (a fixed point) and the mass of their body, due to inertia, retains the second point, which can be considered fixed, while another player impacts their leg with their foot.
Lastly, there is the situation where the bone collapses due to axial pressure.
In this case, there are two situations. On the one hand, the structure of the bone itself can collapse and fracture due to compression. On the other hand, there may be buckling, meaning that due to some inhomogeneity, the bone flexes and ends up deflecting extremely, leading to fracture.
These are the basic mechanisms that can subsequently, in reality, initiate the process, compromising other bones or extending within the same bone, resulting in a more complex fracture.
One situation that may arise is when a deformation force with a fixed point ($F_1$) acts on a bone with properties a body length ($L$), the modulus of Elasticity ($E$), and the moment of inertia of surface ($I_s$), which is fixed at one end.
the strain energy with a fixed point ($W_1$), storing the structure against a stress to deformation with a fixed point ($\sigma_1$), is defined by
the deformation force with a fixed point ($F_1$), the applied force, leads to a stress to deformation with a fixed point ($\sigma_1$) as per
and the stress to deformation with a fixed point ($\sigma_1$), which depends on the outdoor radio ($R_2$), is given by
One possible scenario is that a deformation force with two fixed points ($F_2$) acts on a bone with properties a body length ($L$), the modulus of Elasticity ($E$), and the moment of inertia of surface ($I_s$), which is fixed at both ends:
the strain energy with two fixed points ($W_2$), storing the structure against a movement in flexion with two fixed points ($u_2$), is given by
the deformation force with two fixed points ($F_2$), the applied force, leads to a movement in flexion with two fixed points ($u_2$) as per
and the stress to deformation with two fixed points ($\sigma_2$), which depends on the outdoor radio ($R_2$), is expressed as
One possible scenario is that a deformation force in buckling condition ($F_p$) acts along the axis of the bone with properties a body length ($L$), the modulus of Elasticity ($E$), the buckling factor ($K$), the effective radius ($R$), and the moment of inertia of surface ($I_s$), inducing buckling:
the strain energy in buckling condition ($W_p$), is defined as
the deformation force in buckling condition ($F_p$), the applied force, according to
and the stress to deformation in the case of buckling ($\sigma_p$), which depends on the outdoor radio ($R_2$), is expressed as
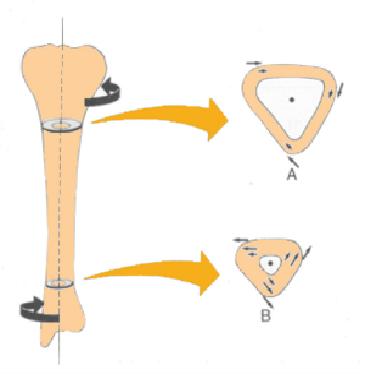
One way to cause a fracture is through bone torsion, which involves applying opposite torques at the ends:
Microscopic elastic deformation corresponds to a modification in the distance between atoms under an external force, without any rearrangement of these atoms.
In general, it's a deformation where the distance changes proportionally to the applied force, referred to as elastic deformation.
Plastic deformation means that if the applied stress is reduced, the material decreases its deformation but ends up with a permanent deformation.
Therefore, if it's subjected to stress again, it generally returns to its elastic form, but due to the new shape, it can't recover its original form.
Plastic deformation involves atoms rearranging themselves, dissociating from existing structures, and forming new bonds that are inherently stable. However, such deformation typically entails a modification in the shape of the material.
Plastic deformation can ultimately lead to changes that may include catastrophic ruptures, which are permanent.
We will work with a bone and with the fall and impact scenarios. The bone parameters and material properties are summarized here:
If a player is impacted in the middle of the bone, considering the foot due to friction and the body due to inertia as fixed points, it results in a load that flexes the bone.
Question of interest: What are the energy, stress, force, displacement, and jump height at which buckling would occur? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
Two situations are considered, fall (break due to buckling, compression or flexion) and impact on the central part of the bone (break due to flexion).
The integration over the section with the inside radio ($R_1$) and the outdoor radio ($R_2$) leads to the introduction of the effective radius ($R$), defined by:
With the outdoor radio ($R_2$) and the inside radio ($R_1$), the body Section ($S$) is defined as
The moment of inertia of surface ($I_s$) is calculated in the case of a cylinder with the outdoor radio ($R_2$) and the inside radio ($R_1$) through
The relationship between the strain energy with two fixed points ($W_2$) and the movement in flexion with two fixed points ($u_2$) in a bending with two fixed points depends on the modulus of Elasticity ($E$), the body length ($L$), and the moment of inertia of surface ($I_s$) is
The relationship between the deformation force with two fixed points ($F_2$) and the movement in flexion with two fixed points ($u_2$) in a bending with two fixed points depends on the modulus of Elasticity ($E$), the body length ($L$), and the moment of inertia of surface ($I_s$). In this context,
The relationship between the stress to deformation with two fixed points ($\sigma_2$) and the deformation force with two fixed points ($F_2$) in a bending with two fixed points depends on the outdoor radio ($R_2$), the body length ($L$), and the moment of inertia of surface ($I_s$). In this context,
The relationship between the strain energy with a fixed point ($W_1$) and the flexion displacement with a fixed point ($u_1$) in a bending with a fixed point depends on the modulus of Elasticity ($E$), the body length ($L$), and the moment of inertia of surface ($I_s$) is:
The relationship between the deformation force with a fixed point ($F_1$) and the flexion displacement with a fixed point ($u_1$) in a bending with a fixed point depends on the modulus of Elasticity ($E$), the body length ($L$), and the moment of inertia of surface ($I_s$) is:
The relationship between the stress to deformation with a fixed point ($\sigma_1$) and the deformation force with a fixed point ($F_1$) in a bending with a fixed point depends on the outdoor radio ($R_2$), the body length ($L$), and the moment of inertia of surface ($I_s$) is
The strain energy in buckling condition ($W_p$) in buckling depends on the modulus of Elasticity ($E$), the body length ($L$), the moment of inertia of surface ($I_s$), the effective radius ($R$), and the buckling factor ($K$) is
The value of the buckling factor ($K$) is:
• 0.5 if both edges are fixed,
• 1.0 if both can rotate,
• 0.7 if one is fixed and the other can rotate, and
• 2.0 if both are free.
The deformation force in buckling condition ($F_p$) in buckling depends on the modulus of Elasticity ($E$), the body length ($L$), the moment of inertia of surface ($I_s$), and the buckling factor ($K$).
The value of the buckling factor ($K$) is:
• 0.5 if both edges are fixed,
• 1.0 if both can rotate,
• 0.7 if one is fixed and the other can rotate, and
• 2.0 if both are free.
The stress to deformation in the case of buckling ($\sigma_p$) in buckling depends on the modulus of Elasticity ($E$), the body length ($L$), the moment of inertia of surface ($I_s$), the body Section ($S$), and the buckling factor ($K$).
The value of the buckling factor ($K$) is:
0.5 if both edges are fixed,
1.0 if both can rotate,
0.7 if one is fixed and the other can rotate, and
2.0 if both are free.
ID:(324, 0)