Plastische Verformung
Storyboard 
Für kleine Verformungen erfährt das Material nur eine elastische Verformung, das heißt, nach dem Entfernen der Last kehrt es in seine ursprüngliche Form zurück. Bei größeren Verformungen können die Atome größere Verschiebungen erfahren, was zu einer dauerhaften Veränderung der Struktur führt. In solchen Fällen sprechen wir von plastischer Verformung.
ID:(324, 0)
Plastische Verformung
Storyboard 
Für kleine Verformungen erfährt das Material nur eine elastische Verformung, das heißt, nach dem Entfernen der Last kehrt es in seine ursprüngliche Form zurück. Bei größeren Verformungen können die Atome größere Verschiebungen erfahren, was zu einer dauerhaften Veränderung der Struktur führt. In solchen Fällen sprechen wir von plastischer Verformung.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
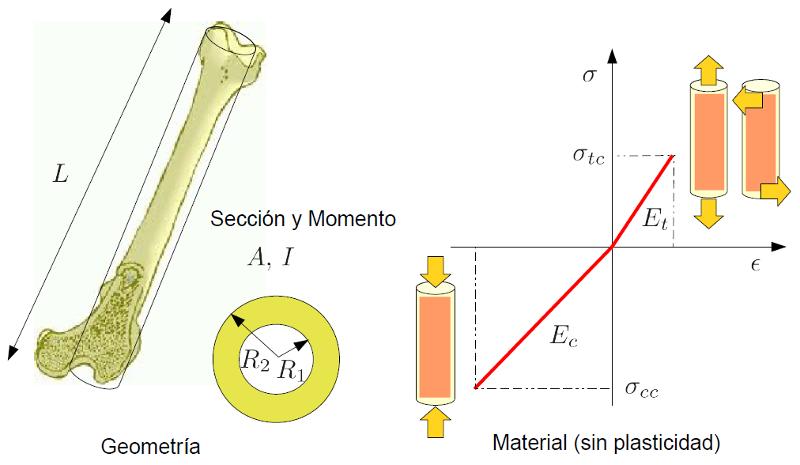
Der Knochen kann als Hohlzylinder modelliert werden, da das Material im Inneren keine bedeutende Last tragen kann. Daher wird er geometrisch als Zylinder mit den Eigenschaften der Körperlänge ($L$), der Inner Radius ($R_1$) und der Außenwerbung Radio ($R_2$) dargestellt:
Daher ist der Wirkungsradius ($R$)
die Körper Sektion ($S$) ist
und der Trägheitsmoment der Fläche ($I_s$) ist
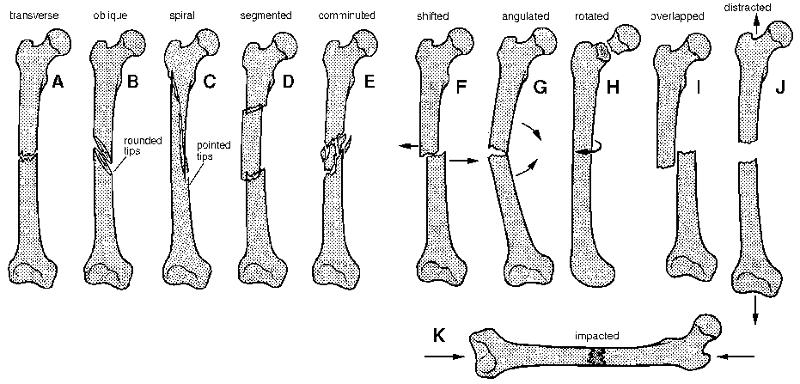
Im Fall des Knochens gibt es verschiedene Situationen, die zu extremen Spannungen f hren und zu Br chen f hren k nnen.
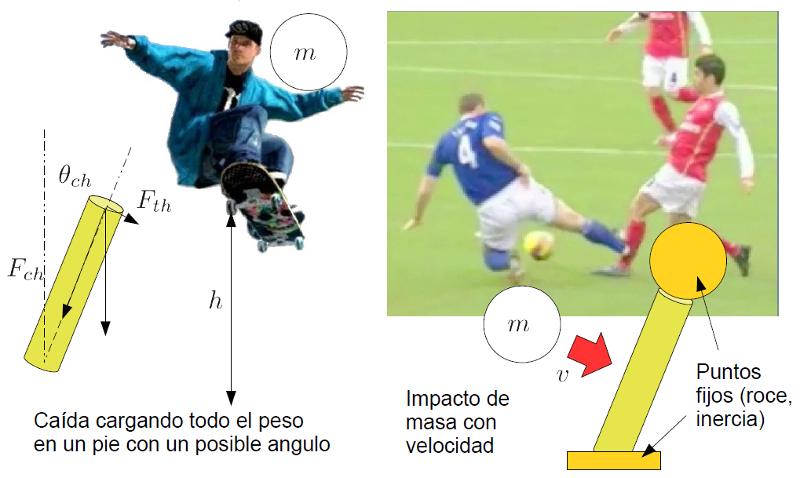
Eine Situation ist, wenn der Knochen an einem Ende fixiert ist und vom anderen aus gebogen wird:
Ein Beispiel ist, wenn eine Person f llt und sich an einem Punkt abst tzt, wodurch ein fester Punkt durch Reibung entsteht, w hrend der Schwerpunkt aufgrund der Tr gheit weiterhin wandert und den Knochen biegt, bis er bricht.
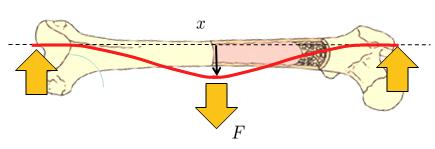
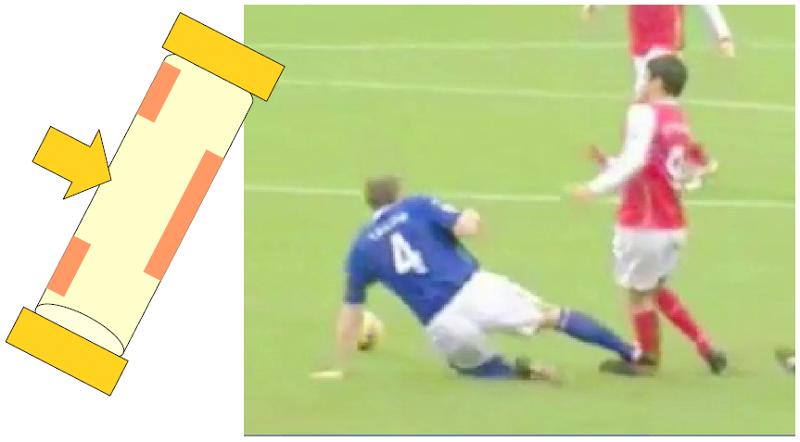
Eine andere Situation ist, wenn er an beiden Enden fixiert ist und eine senkrechte Kraft an einer Zwischenposition erh lt:
Ein typisches Beispiel daf r ist, wenn ein Fu ballspieler seinen Fu (einen festen Punkt) aufsetzt und die Masse seines K rpers durch Tr gheit den zweiten Punkt, der als fest betrachtet werden kann, beibeh lt, w hrend ein anderer Spieler mit seinem Fu gegen das Bein des Spielers st t.
Schlie lich gibt es die Situation, in der der Knochen durch axiale Druckbelastung zusammenbricht.
In diesem Fall gibt es zwei Situationen. Einerseits kann die Struktur des Knochens selbst zusammenbrechen und durch Kompression brechen. Andererseits kann es zu Knicken kommen, was bedeutet, dass der Knochen aufgrund einer Ungleichm igkeit beugt und sich extrem ablenkt, was zu einem Bruch f hrt.
Dies sind die grundlegenden Mechanismen, die sp ter in der Realit t den Prozess ausl sen k nnen, andere Knochen gef hrden oder sich innerhalb desselben Knochens ausdehnen und zu einem komplexeren Bruch f hren k nnen.
Eine Situation, die auftreten kann, ist, wenn eine Verformungskraft mit Fixpunkt ($F_1$) auf einen Knochen mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$) und der Trägheitsmoment der Fläche ($I_s$) wirkt, der an einem Ende fixiert ist.
die Dehnungsenergie mit Fixpunkt ($W_1$), der die Struktur gegen eine Spannung zur Verformung mit einem festen Punkt ($\sigma_1$) speichert, ist definiert durch
die Verformungskraft mit Fixpunkt ($F_1$), die angewendete Kraft, f hrt zu eine Spannung zur Verformung mit einem festen Punkt ($\sigma_1$) gem
und die Spannung zur Verformung mit einem festen Punkt ($\sigma_1$), das von der Außenwerbung Radio ($R_2$) abh ngt, ist gegeben durch
Eine m gliche Situation ist, dass eine Verformungskraft mit zwei Fixpunkten ($F_2$) auf einen Knochen mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$) und der Trägheitsmoment der Fläche ($I_s$) wirkt, der an beiden Enden fixiert ist:
die Dehnungsenergie mit zwei Fixpunkten ($W_2$), der die Struktur gegen ein Bewegung in Flexion mit zwei Fixpunkten ($u_2$) speichert, ist gegeben durch
die Verformungskraft mit zwei Fixpunkten ($F_2$), die angewendete Kraft, f hrt zu ein Bewegung in Flexion mit zwei Fixpunkten ($u_2$) gem
und die Spannung zur Verformung mit zwei Fixpunkten ($\sigma_2$), das von der Außenwerbung Radio ($R_2$) abh ngt, ist ausgedr ckt als
Ein m gliches Szenario ist, dass eine Verformungskraft im Knickzustand ($F_p$) entlang der Achse des Knochens mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$), der Knickfaktor ($K$), der Wirkungsradius ($R$) und der Trägheitsmoment der Fläche ($I_s$) wirkt und dadurch ein Knicken verursacht:
die Dehnungsenergie im Knickzustand ($W_p$), wird definiert als
die Verformungskraft im Knickzustand ($F_p$), die angewendete Kraft, f hrt gem
und die Verformungsspannung bei Knickung ($\sigma_p$), das von der Außenwerbung Radio ($R_2$) abh ngt, wird ausgedr ckt als
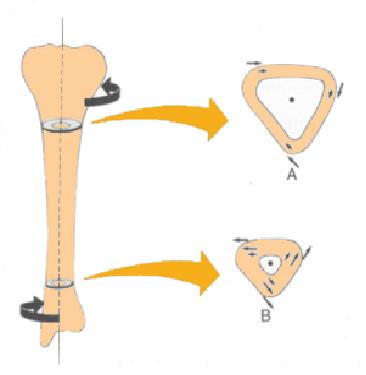
Eine M glichkeit, einen Knochenbruch zu verursachen, ist durch Knochenverdrehung, was das Anwenden entgegengesetzter Drehmomente an den Enden beinhaltet:
Mikroskopische elastische Verformung entspricht einer Modifikation des Abstands zwischen den Atomen unter einer externen Kraft, ohne dass eine Neuordnung dieser Atome erfolgt.
Im Allgemeinen handelt es sich um eine Verformung, bei der der Abstand proportional zur angewandten Kraft ver ndert wird, und man spricht von einer elastischen Verformung.
Plastische Verformung bedeutet, dass sich das Material bei Reduzierung der angelegten Spannung zwar weniger verformt, aber eine bleibende Verformung aufweist.
Daher kehrt es bei erneuter Belastung in der Regel in seine elastische Form zur ck, kann jedoch aufgrund der neuen Form nicht seine urspr ngliche Form wiedererlangen.
Plastische Verformung bedeutet, dass sich Atome neu ordnen, sich von bestehenden Strukturen l sen und neue Bindungen bilden, die an sich stabil sind. Diese Verformung f hrt jedoch in der Regel zu einer Modifikation der Form des Materials.
Plastische Verformung kann letztendlich zu Ver nderungen f hren, die katastrophale Br che einschlie en k nnen, die permanent sind.
Wir werden mit einem Knochen und mit den Sturz- und Aufprallszenarien arbeiten. Die Knochenparameter und Materialeigenschaften sind hier zusammengefasst:
Wenn ein Spieler in der Mitte des Knochens getroffen wird und angenommen wird, dass der Fu aufgrund von Reibung und der K rper aufgrund von Tr gheit feste Punkte sind, entsteht eine Belastung, die den Knochen biegt.
Interessante Frage: Welche Energie, Spannung, Kraft, Verschiebung und Sprungh he w rden zu einem Knicken f hren? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
Es werden zwei Situationen betrachtet: Sturz (Bruch aufgrund von Knicken, Kompression oder Beugung) und Aufprall auf den zentralen Teil des Knochens (Bruch aufgrund von Beugung).
Die Integration ber den Abschnitt mit der Inner Radius ($R_1$) und der Außenwerbung Radio ($R_2$) f hrt zur Einf hrung von der Wirkungsradius ($R$), definiert durch:
Mit der Außenwerbung Radio ($R_2$) und der Inner Radius ($R_1$), ist die Körper Sektion ($S$) definiert als
Der Trägheitsmoment der Fläche ($I_s$) wird im Fall eines Zylinders mit der Außenwerbung Radio ($R_2$) und der Inner Radius ($R_1$) durch
Die Beziehung zwischen die Dehnungsenergie mit zwei Fixpunkten ($W_2$) und der Bewegung in Flexion mit zwei Fixpunkten ($u_2$) in einer Biegung mit zwei festen Punkten h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab ist
Die Beziehung zwischen die Verformungskraft mit zwei Fixpunkten ($F_2$) und der Bewegung in Flexion mit zwei Fixpunkten ($u_2$) bei einer Biegung mit zwei festen Punkten h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab. In diesem Kontext,
Die Beziehung zwischen die Spannung zur Verformung mit zwei Fixpunkten ($\sigma_2$) und die Verformungskraft mit zwei Fixpunkten ($F_2$) in einer Biegung mit zwei festen Punkten h ngt von der Außenwerbung Radio ($R_2$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab. In diesem Kontext,
Die Beziehung zwischen die Dehnungsenergie mit Fixpunkt ($W_1$) und der Flexionsverschiebung mit Fixpunkt ($u_1$) in einer Biegung mit einem festen Punkt h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab:
Die Beziehung zwischen die Verformungskraft mit Fixpunkt ($F_1$) und der Flexionsverschiebung mit Fixpunkt ($u_1$) in einer Biegung mit einem festen Punkt h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab:
Die Beziehung zwischen die Spannung zur Verformung mit einem festen Punkt ($\sigma_1$) und die Verformungskraft mit Fixpunkt ($F_1$) in einer Biegung mit einem festen Punkt h ngt von der Außenwerbung Radio ($R_2$), der Körperlänge ($L$) und der Trägheitsmoment der Fläche ($I_s$) ab.
Die Dehnungsenergie im Knickzustand ($W_p$) beim Beulen h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$), der Trägheitsmoment der Fläche ($I_s$), der Wirkungsradius ($R$) und der Knickfaktor ($K$) ab
Der Wert von der Knickfaktor ($K$) ist:
• 0,5, wenn beide Kanten fest sind,
• 1,0, wenn beide drehbar sind,
• 0,7, wenn eine fest ist und die andere drehbar ist, und
• 2,0, wenn beide frei sind.
Die Verformungskraft im Knickzustand ($F_p$) beim Beulen h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$), der Trägheitsmoment der Fläche ($I_s$) und der Knickfaktor ($K$) ab.
Der Wert von der Knickfaktor ($K$) ist:
• 0,5, wenn beide Kanten fest sind,
• 1,0, wenn beide drehbar sind,
• 0,7, wenn eine fest ist und die andere drehbar ist, und
• 2,0, wenn beide frei sind.
Die Verformungsspannung bei Knickung ($\sigma_p$) beim Beulen h ngt von der Elastizitätsmodul ($E$), der Körperlänge ($L$), der Trägheitsmoment der Fläche ($I_s$), die Körper Sektion ($S$) und der Knickfaktor ($K$) ab.
Der Wert von der Knickfaktor ($K$) ist:
• 0,5, wenn beide Kanten fest sind,
• 1,0, wenn beide drehbar sind,
• 0,7, wenn eine fest ist und die andere drehbar ist, und
• 2,0, wenn beide frei sind.
ID:(324, 0)