Usuario:
Primera ley de la termodinámica
Storyboard 
La primera ley de la termodinámica establece que la energía se conserva y se compone de dos partes: una asociada al trabajo y otra al calor. A diferencia del trabajo, esta última parte no puede transformarse completamente en trabajo, lo que limita las conversiones energéticas posibles.
ID:(1398, 0)
Mecanismos
Iframe
La primera ley de la termodinámica, o ley de conservación de la energía, establece que la energía no puede ser creada ni destruida en un sistema aislado; solo puede ser transferida o transformada. Este principio afirma que la energía total de un sistema aislado permanece constante. En términos prácticos, esto significa que el cambio en la energía interna de un sistema es igual al calor añadido al sistema menos el trabajo realizado por el sistema. La energía interna abarca la energía total dentro de un sistema, incluyendo la energía cinética y potencial a nivel molecular. El calor es la energía transferida entre sistemas debido a una diferencia de temperatura, mientras que el trabajo es la energía transferida cuando una fuerza se aplica sobre una distancia, a menudo relacionada con cambios de volumen en los gases. La primera ley es fundamental para analizar la eficiencia de los motores térmicos, el rendimiento de los sistemas de refrigeración y calefacción, y para entender los procesos metabólicos en los sistemas biológicos. Proporciona una base para comprender las transferencias y transformaciones de energía en diversos procesos físicos, asegurando que la energía dentro de un sistema aislado siempre se conserve.
Mecanismos
ID:(15250, 0)
Conservación de energía
Concepto
La primera ley de la termodinámica establece que la energía siempre se conserva.
Mientras que en la mecánica se enuncia una conservación similar restringida a sistemas no disipativos (por ejemplo, excluyendo el rozamiento), en la termodinámica se generaliza considerando no solo el trabajo mecánico, sino también el calor generado o absorbido por el sistema.
En este sentido, la conservación de la energía postulada en la termodinámica no tiene restricciones y es aplicable a todos los sistemas, siempre y cuando se consideren todos los intercambios y conversiones de energía posibles.
ID:(37, 0)
Primera ley de la termodinámica
Concepto
La primera ley de la termodinámica se desarrolla a partir de varios trabajos [1,2], estableciendo que la energía se conserva, es decir, que el diferencial de la energía interna ($dU$) siempre es igual a el diferencial inexacto del calor ($\delta Q$) suministrado al sistema (positivo) menos el diferencial inexacto del trabajo ($\delta W$) realizado por el sistema (negativo).
Por lo tanto, tenemos:
| $ dU = \delta Q - \delta W $ |
Mientras que el diferencial exacto no depende de cómo se ejecuta la variación, el diferencial inexacto sí lo hace. Cuando nos referimos a un diferencial sin especificar que es inexacto, se asume que es exacto.
[1] "Über die quantitative und qualitative Bestimmung der Kräfte" (Sobre la determinación cualitativa y cuantitativa de la Fuerza), Julius Robert von Mayer, Annalen der Chemie und Pharmacie, 1842
[2] "Über die Erhaltung der Kraft" (Sobre la conservación de la Fuerza), Hermann von Helmholtz, 1847
ID:(15700, 0)
Presión y trabajo
Descripción
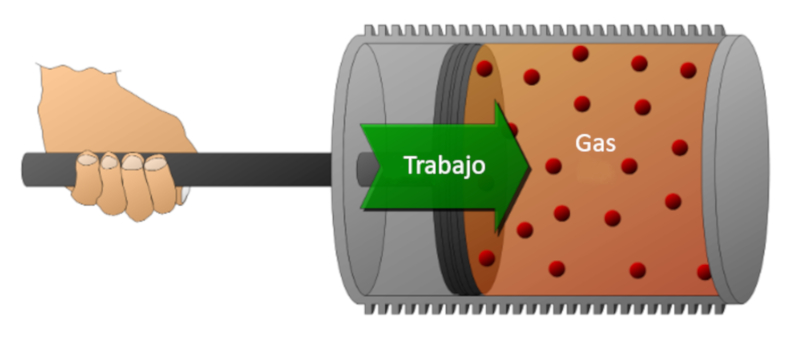
Consideremos un gas en un cilindro en el cual se puede desplazar un pistón. Si se desplaza el pistón, es posible reducir el volumen comprimiendo el gas. Para realizar esta compresión se requiere de energía, la cual es igual a la fuerza ejercida por el gas multiplicada por la distancia que recorre el pistón. Esta energía también puede representarse en función de la presión, ya que ésta se define por la fuerza y la superficie del pistón.
El trabajo puede realizarse sobre el sistema (compresión) o por el sistema sobre el medio externo (expansión).
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($dV$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuación para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \delta W = F dx $ |
Así que puede ser escrita como:
| $ \delta W = p dV $ |
ID:(11126, 0)
Primera ley de la termodinámica y la presión
Concepto
Dado que el diferencial de la energía interna ($dU$) se relaciona con el diferencial inexacto del calor ($\delta Q$) y el diferencial inexacto del trabajo ($\delta W$) como se muestra a continuación:
| $ dU = \delta Q - \delta W $ |
Y sabiendo que el diferencial inexacto del trabajo ($\delta W$) está relacionado con la presión ($p$) y la variación del volumen ($dV$) de la siguiente manera:
| $ \delta W = p dV $ |
Entonces podemos concluir que:
| $ dU = \delta Q - p dV $ |
ID:(15701, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ dU = \delta Q - \delta W $
dU = dQ - dW
$ dU = \delta Q - p dV $
dU = dQ - p * dV
$ dV = S dx $
DV = S * Ds
$ \delta W = F dx $
dW = F * dx
$ \delta W = p dV $
dW = p * dV
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
ID:(15309, 0)
Primera ley de la termodinámica
Ecuación
El diferencial de la energía interna ($dU$) siempre es igual a la cantidad de el diferencial inexacto del calor ($\delta Q$) suministrada al sistema (positiva) menos la cantidad de el diferencial inexacto del trabajo ($\delta W$) realizada por el sistema (negativa):
| $ dU = \delta Q - \delta W $ |
ID:(9632, 0)
Trabajo
Ecuación
La relación entre el trabajo y nuestra acción está vinculada a la dependencia de el diferencial inexacto del trabajo ($\delta W$) respecto a la distancia recorrida. Si consideramos una fuerza mecánica ($F$) para mover un objeto a lo largo de un camino recorrido ($dx$), la energía requerida puede expresarse como:
| $ \delta W = F dx $ |
La notación $\delta W$ se utiliza para indicar la variación del trabajo, a diferencia de $dW$, que nos recuerda que su valor depende del proceso de variación de la longitud $dx$. Un ejemplo de esto sería si el desplazamiento ocurriera en un gas y se produjera un cambio en este, en cuyo caso:
$\delta W < Fdx$
ID:(3202, 0)
Definición de la presión
Ecuación
La presión de la columna de agua ($p$) se calcula a partir de la fuerza de la columna ($F$) y la sección de la columna ($S$) de la siguiente manera:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Elemento de volumen
Ecuación
Si tenemos un tubo con una la sección del tubo ($S$) que se desplaza una distancia el elemento del tubo ($\Delta s$) a lo largo de su eje, habiendo trasladado el elemento de volumen ($\Delta V$), igual a:
| $ dV = S dx $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 0)
Presión y trabajo
Ecuación
El diferencial inexacto del trabajo ($\delta W$) es igual a la presión ($p$) multiplicado por la variación del volumen ($dV$):
| $ \delta W = p dV $ |
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($dV$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuación para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \delta W = F dx $ |
Así que puede ser escrita como:
| $ \delta W = p dV $ |
ID:(3468, 0)
Primera ley de la termodinámica y la presión
Ecuación
Con la primera ley de la termodinámica, se puede expresar en términos de el diferencial de la energía interna ($dU$), el diferencial inexacto del calor ($\delta Q$), la presión ($p$) y la variación del volumen ($dV$) como:
| $ dU = \delta Q - p dV $ |
Dado que el diferencial de la energía interna ($dU$) se relaciona con el diferencial inexacto del calor ($\delta Q$) y el diferencial inexacto del trabajo ($\delta W$) como se muestra a continuación:
| $ dU = \delta Q - \delta W $ |
Y sabiendo que el diferencial inexacto del trabajo ($\delta W$) está relacionado con la presión ($p$) y la variación del volumen ($dV$) de la siguiente manera:
| $ \delta W = p dV $ |
Entonces podemos concluir que:
| $ dU = \delta Q - p dV $ |
ID:(3470, 0)