La premi re loi de la thermodynamique, galement connue sous le nom de loi de la conservation de l' nergie, stipule que l' nergie ne peut ni tre cr e ni d truite dans un syst me isol ; elle peut seulement tre transf r e ou transform e. Ce principe affirme que l' nergie totale d'un syst me isol reste constante. En termes pratiques, cela signifie que la variation de l' nergie interne d'un syst me est gale la chaleur ajout e au syst me moins le travail effectu par le syst me. L' nergie interne englobe l' nergie totale contenue dans un syst me, y compris l' nergie cin tique et potentielle au niveau mol culaire. La chaleur est l' nergie transf r e entre des syst mes en raison d'une diff rence de temp rature, tandis que le travail est l' nergie transf r e lorsqu'une force est appliqu e sur une distance, souvent li e des changements de volume dans les gaz. La premi re loi est fondamentale pour analyser l'efficacit des moteurs thermiques, la performance des syst mes de r frig ration et de chauffage et pour comprendre les processus m taboliques dans les syst mes biologiques. Elle fournit une base pour comprendre les transferts et les transformations d' nergie dans divers processus physiques, garantissant que l' nergie l'int rieur d'un syst me isol est toujours conserv e.

mechanisms

La premi re loi de la thermodynamique tablit que l' nergie est toujours conserv e.

Alors qu'en m canique, on observe une conservation similaire, limit e aux syst mes non dissipatifs (par exemple, en excluant le frottement), la thermodynamique g n ralise cette notion en prenant en compte non seulement le travail m canique, mais aussi la chaleur g n r e ou absorb e par le syst me.

Dans ce sens, la conservation de l' nergie telle que postul e en thermodynamique n\'a aucune restriction et s\'applique tous les syst mes, tant que toutes les changes et conversions d\' nergie possibles sont prises en compte.

La premi re loi de la thermodynamique a t d velopp e travers divers travaux [1,2], tablissant que l' nergie se conserve. Cela signifie que le différentiel d'énergie interne ($dU$) est toujours gal le différence de chaleur inexacte ($\delta Q$) fourni au syst me (positif) moins le différentiel de travail inexact ($\delta W$) r alis par le syst me (n gatif).

Par cons quent, nous avons :

equation=9632

Alors que le diff rentiel exact ne d pend pas de la mani re dont la variation est ex cut e, le diff rentiel inexact, lui, en d pend. Lorsque nous nous r f rons un diff rentiel sans pr ciser qu'il est inexact, il est suppos tre exact.

[1] " ber die quantitative und qualitative Bestimmung der Kr fte" (Sur la D termination Quantitative et Qualitative des Forces), Julius Robert von Mayer, Annalen der Chemie und Pharmacie, 1842

[2] " ber die Erhaltung der Kraft" (Sur la Conservation de la Force), Hermann von Helmholtz, 1847

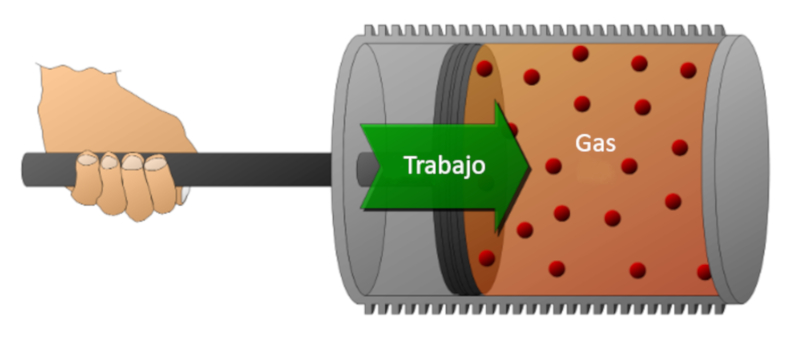
Consid rons un gaz dans un cylindre o un piston peut se d placer. Si le piston est d plac , il est possible de r duire le volume en comprimant le gaz. Pour r aliser cette compression, de l' nergie est n cessaire, quivalente la force exerc e par le gaz multipli e par la distance parcourue par le piston. Cette nergie peut galement tre repr sent e en fonction de la pression, puisque la pression est d finie par la force et la surface du piston.

image

Le travail peut tre effectu sur le syst me (compression) ou par le syst me sur l'environnement externe (expansion).

tant donn que a force mécanique ($F$) divis par a section ($S$) est gal a pression ($p$) :

equation=4342,0

et que a variation de volume ($\Delta V$) avec le distance parcourue ($dx$) est gal :

equation=4346,0

L' quation pour le différentiel de travail inexact ($\delta W$) peut tre exprim e comme suit :

equation=3202

Elle peut donc tre crite comme :

equation=3468

tant donn que le différentiel d'énergie interne ($dU$) est en relation avec le différence de chaleur inexacte ($\delta Q$) et le différentiel de travail inexact ($\delta W$) comme illustr ci-dessous :

equation=9632

Et il est connu que le différentiel de travail inexact ($\delta W$) est li a pression ($p$) et a variation de volume ($\Delta V$) comme suit :

equation=3468

Par cons quent, nous pouvons en conclure que :

equation=3470

model

Le différentiel d'énergie interne ($dU$) est toujours gal la quantit de le différence de chaleur inexacte ($\delta Q$) fournie au syst me (positif) moins la quantit de le différentiel de travail inexact ($\delta W$) r alis e par le syst me (n gatif) :

kyon

A écart de travail ($\Delta W$) est défini comme le produit de a force à masse constante ($F$) et a distance parcourue en un temps ($\Delta s$) :

kyon

A pression de la colonne d'eau ($p$) se calcule partir de a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) comme suit :

kyon

Si nous avons un tube avec une a section de tube ($S$) se d pla ant sur une distance le élément tubulaire ($\Delta s$) le long de son axe, ayant d plac le élément de volume ($\Delta V$), alors cela gal :

kyon

Le différentiel de travail inexact ($\delta W$) est gal a pression ($p$) multipli par a variation de volume ($\Delta V$)xa0:

kyon

Avec la premi re loi de la thermodynamique, cela peut tre exprim en termes de le différentiel d'énergie interne ($dU$), le différence de chaleur inexacte ($\delta Q$), a pression ($p$) et a variation de volume ($\Delta V$) comme suit :

kyon