Erster Hauptsatz der Thermodynamik
Storyboard 
Das erste Gesetz der Thermodynamik besagt, dass Energie erhalten bleibt und sich aus zwei Komponenten zusammensetzt: einer, die mit Arbeit verbunden ist, und einer anderen, die mit Wärme verbunden ist. Im Gegensatz zur Arbeit kann dieser letztere Teil nicht vollständig in Arbeit umgewandelt werden, was die möglichen Energieumwandlungen einschränkt.
ID:(1398, 0)
Erster Hauptsatz der Thermodynamik
Storyboard 
Das erste Gesetz der Thermodynamik besagt, dass Energie erhalten bleibt und sich aus zwei Komponenten zusammensetzt: einer, die mit Arbeit verbunden ist, und einer anderen, die mit Wärme verbunden ist. Im Gegensatz zur Arbeit kann dieser letztere Teil nicht vollständig in Arbeit umgewandelt werden, was die möglichen Energieumwandlungen einschränkt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Da die Mechanische Kraft ($F$) geteilt durch die Abschnitt ($S$) gleich die Druck ($p$) ist:
und die Volumenvariation ($\Delta V$) mit der Zurückgelegter Weg ($dx$) gleich ist:
Die Gleichung f r der Differential ungenaue Arbeits ($\delta W$) kann wie folgt ausgedr ckt werden:
Daher kann sie geschrieben werden als:
Da der Interne Energiedifferenz ($dU$) in Beziehung zu der Differential ungenau Wärme ($\delta Q$) und der Differential ungenaue Arbeits ($\delta W$) steht, wie unten gezeigt:
Und es ist bekannt, dass der Differential ungenaue Arbeits ($\delta W$) in Beziehung zu die Druck ($p$) und die Volumenvariation ($\Delta V$) steht, wie folgt:
Daher k nnen wir schlussfolgern, dass:
Beispiele
Das erste Gesetz der Thermodynamik, auch als Gesetz der Energieerhaltung bekannt, besagt, dass Energie in einem isolierten System weder erschaffen noch zerst rt werden kann; sie kann nur bertragen oder umgewandelt werden. Dieses Prinzip besagt, dass die Gesamtenergie eines isolierten Systems konstant bleibt. In praktischen Begriffen bedeutet dies, dass die nderung der inneren Energie eines Systems gleich der hinzugef gten W rme abz glich der vom System geleisteten Arbeit ist. Die innere Energie umfasst die gesamte Energie innerhalb eines Systems, einschlie lich der kinetischen und potenziellen Energie auf molekularer Ebene. W rme ist die Energie, die zwischen Systemen aufgrund eines Temperaturunterschieds bertragen wird, w hrend Arbeit die Energie ist, die bertragen wird, wenn eine Kraft ber eine Strecke ausge bt wird, oft in Zusammenhang mit Volumen nderungen in Gasen. Das erste Gesetz ist grundlegend f r die Analyse der Effizienz von W rmekraftmaschinen, die Leistung von K hl- und Heizsystemen und das Verst ndnis von Stoffwechselprozessen in biologischen Systemen. Es bildet die Grundlage f r das Verst ndnis von Energie bertragungen und -umwandlungen in verschiedenen physikalischen Prozessen und stellt sicher, dass die Energie innerhalb eines isolierten Systems immer erhalten bleibt.
Das erste Gesetz der Thermodynamik besagt, dass Energie immer erhalten bleibt.
W hrend in der Mechanik eine hnliche Erhaltung formuliert wird, die auf nicht dissipative Systeme beschr nkt ist (zum Beispiel unter Ausschluss von Reibung), generalisiert die Thermodynamik dies, indem sie nicht nur die mechanische Arbeit, sondern auch die vom System erzeugte oder absorbierte W rme ber cksichtigt.
In diesem Sinne gibt es keine Einschr nkungen f r die in der Thermodynamik postulierte Energieerhaltung und sie gilt f r alle Systeme, solange alle m glichen Energieaustausche und -umwandlungen ber cksichtigt werden.
Das erste Gesetz der Thermodynamik wurde durch verschiedene Arbeiten [1,2] entwickelt und besagt, dass Energie erhalten bleibt. Das bedeutet, dass der Interne Energiedifferenz ($dU$) immer gleich der Differential ungenau Wärme ($\delta Q$) ist, das dem System zugef hrt wird (positiv), abz glich der Differential ungenaue Arbeits ($\delta W$), das vom System geleistet wird (negativ).
Daher haben wir:
W hrend das exakte Differential nicht davon abh ngt, wie die Variation ausgef hrt wird, h ngt das inexakte Differential davon ab. Wenn wir uns auf ein Differential beziehen, ohne anzugeben, dass es inexact ist, wird angenommen, dass es exakt ist.
![]() [1] " ber die quantitative und qualitative Bestimmung der Kr fte", Julius Robert von Mayer, Annalen der Chemie und Pharmacie, 1842
[1] " ber die quantitative und qualitative Bestimmung der Kr fte", Julius Robert von Mayer, Annalen der Chemie und Pharmacie, 1842
![]() [2] " ber die Erhaltung der Kraft", Hermann von Helmholtz, 1847
[2] " ber die Erhaltung der Kraft", Hermann von Helmholtz, 1847
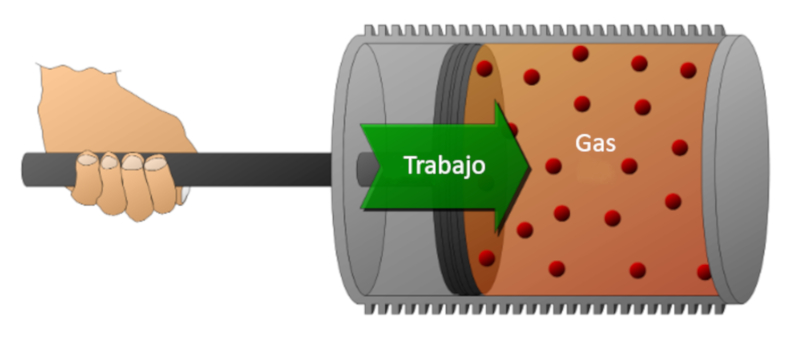
Betrachten wir ein Gas in einem Zylinder, in dem sich ein Kolben bewegen kann. Wenn der Kolben bewegt wird, kann das Gasvolumen durch Kompression verringert werden. F r diese Kompression wird Energie ben tigt, die gleich der vom Gas ausge bten Kraft multipliziert mit der zur ckgelegten Strecke des Kolbens ist. Diese Energie kann auch in Bezug auf den Druck dargestellt werden, da Druck durch die Kraft und den Querschnitt des Kolbens definiert wird.
Arbeit kann am System geleistet werden (Kompression) oder vom System auf die externe Umgebung bertragen werden (Expansion).
Da die Mechanische Kraft ($F$) geteilt durch die Abschnitt ($S$) gleich die Druck ($p$) ist:
und die Volumenvariation ($\Delta V$) mit der Zurückgelegter Weg ($dx$) gleich ist:
Die Gleichung f r der Differential ungenaue Arbeits ($\delta W$) kann wie folgt ausgedr ckt werden:
Daher kann sie geschrieben werden als:
Da der Interne Energiedifferenz ($dU$) in Beziehung zu der Differential ungenau Wärme ($\delta Q$) und der Differential ungenaue Arbeits ($\delta W$) steht, wie unten gezeigt:
Und es ist bekannt, dass der Differential ungenaue Arbeits ($\delta W$) in Beziehung zu die Druck ($p$) und die Volumenvariation ($\Delta V$) steht, wie folgt:
Daher k nnen wir schlussfolgern, dass:
Der Interne Energiedifferenz ($dU$) ist immer gleich der Menge von der Differential ungenau Wärme ($\delta Q$), die dem System zugef hrt wird (positiv), abz glich der Menge von der Differential ungenaue Arbeits ($\delta W$), die vom System durchgef hrt wird (negativ):
Die Arbeits Varianz ($\Delta W$) wird als das Produkt von die Kraft mit konstanter Masse ($F$) und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) definiert:
Die Druck der Wassersäule ($p$) wird aus die Kraft der Säule ($F$) und die Column Abschnitt ($S$) wie folgt berechnet:
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
Der Differential ungenaue Arbeits ($\delta W$) ist gleich die Druck ($p$) multipliziert mit die Volumenvariation ($\Delta V$):
Mit dem ersten Hauptsatz der Thermodynamik kann dies in Bezug auf der Interne Energiedifferenz ($dU$), der Differential ungenau Wärme ($\delta Q$), die Druck ($p$) und die Volumenvariation ($\Delta V$) ausgedr ckt werden als:
ID:(1398, 0)