Mit konstanter Beschleunigung abfangen
Storyboard 
Objekte können sich kreuzen, wenn sie zum gleichen Zeitpunkt an derselben Position übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Ausgangspunkten und Geschwindigkeiten aus bewegen und Beschleunigungen erfahren, die es ihnen ermöglichen, am Ende der Reise in Position und Zeit übereinzustimmen.
ID:(1412, 0)
Mit konstanter Beschleunigung abfangen
Storyboard 
Objekte können sich kreuzen, wenn sie zum gleichen Zeitpunkt an derselben Position übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Ausgangspunkten und Geschwindigkeiten aus bewegen und Beschleunigungen erfahren, die es ihnen ermöglichen, am Ende der Reise in Position und Zeit übereinzustimmen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
und der Abgelaufene Zeit ($\Delta t$) als
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
und der Abgelaufene Zeit ($\Delta t$) als
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
Daraus folgt:
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
Daraus folgt:
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
und
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
innerhalb dieses Zeitintervalls definiert.
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
und
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
innerhalb dieses Zeitintervalls definiert.
Beispiele
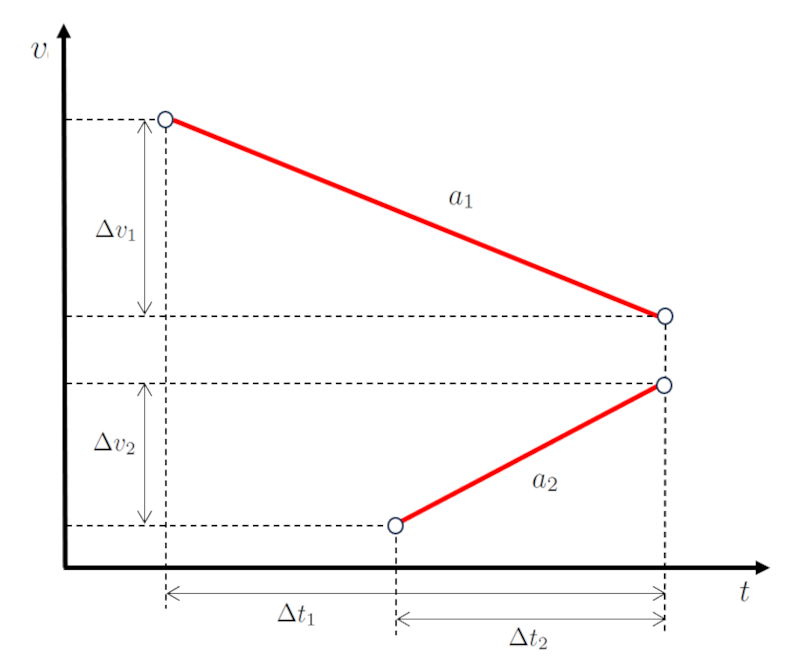
In einem Szenario mit der Bewegung von zwei K rpern ndert der erste seine Geschwindigkeit um die Geschwindigkeitsunterschied des ersten Körpers ($\Delta v_1$) w hrend eine Reisezeit des ersten Objekts ($\Delta t_1$) mit die Erste Körperbeschleunigung ($a_1$).
Anschlie end bewegt sich der zweite K rper vorw rts und ndert seine Geschwindigkeit um die Geschwindigkeitsunterschied des zweiten Körpers ($\Delta v_2$) w hrend eines Zeitraums von die Reisezeit des zweiten Objekts ($\Delta t_2$) mit die Beschleunigung des zweiten Körpers ($a_2$).
Wenn dies grafisch dargestellt wird, erhalten wir ein Geschwindigkeits-Zeit-Diagramm wie unten gezeigt:
Der Schl ssel hierbei ist, dass die Werte die Geschwindigkeitsunterschied des ersten Körpers ($\Delta v_1$) und die Geschwindigkeitsunterschied des zweiten Körpers ($\Delta v_2$) sowie die Werte die Reisezeit des ersten Objekts ($\Delta t_1$) und die Reisezeit des zweiten Objekts ($\Delta t_2$) so gew hlt sind, dass sich beide K rper am gleichen Ort und zur gleichen Zeit treffen.
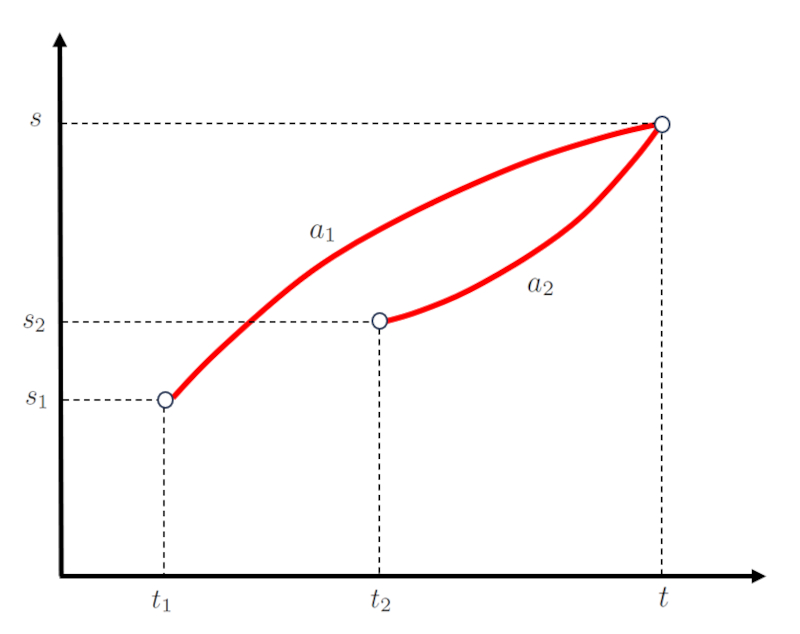
Im Falle von zwei K rpern kann die Bewegung des ersten durch eine Funktion beschrieben werden, die die Punkte der Anfangszeit des ersten Objekts ($t_1$), der Kreuzungszeit ($t$), die Anfangsgeschwindigkeit des ersten Körpers ($v_{01}$) und die Endgeschwindigkeit des ersten Körpers ($v_1$) involviert, dargestellt durch eine Gerade mit einer Steigung von die Erste Körperbeschleunigung ($a_1$):
F r die Bewegung des zweiten K rpers, definiert durch die Punkte die Anfangsgeschwindigkeit des zweiten Körpers ($v_{02}$), die Endgeschwindigkeit des zweiten Körpers ($v_2$), der Anfangszeit des zweiten Objekts ($t_2$) und der Kreuzungszeit ($t$), wird eine zweite Gerade mit einer Steigung von die Beschleunigung des zweiten Körpers ($a_2$) verwendet:
Dies wird wie folgt dargestellt:
Im Falle einer Bewegung von zwei K rpern stimmt die Position, an der die Bahn des ersten K rpers endet, mit der des zweiten K rpers bei die Kreuzungsposition ($s$) berein.
Ebenso stimmt die Zeit, zu der die Bahn des ersten K rpers endet, mit der des zweiten K rpers bei der Kreuzungszeit ($t$) berein.
F r den ersten K rper h ngt die Kreuzungsposition ($s$) von die Anfangsposition des ersten Objekts ($s_1$), die Anfangsgeschwindigkeit des ersten Körpers ($v_{01}$), die Erste Körperbeschleunigung ($a_1$), der Anfangszeit des ersten Objekts ($t_1$) ab, wie folgt:
W hrend f r den zweiten K rper die Kreuzungsposition ($s$) von die Anfangsposition des zweiten Objekts ($s_2$), die Anfangsgeschwindigkeit des zweiten Körpers ($v_{02}$), die Beschleunigung des zweiten Körpers ($a_2$), der Anfangszeit des zweiten Objekts ($t_2$) abh ngt, wie folgt:
Dies wird wie folgt dargestellt:
Beschleunigung entspricht der nderung der Geschwindigkeit pro Zeiteinheit.
Deshalb ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) in Abh ngigkeit von die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) wie folgt zu definieren:
Beschleunigung entspricht der nderung der Geschwindigkeit pro Zeiteinheit.
Deshalb ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) in Abh ngigkeit von die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) wie folgt zu definieren:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
Das Verh ltnis, in dem die Geschwindigkeits nderung im Laufe der Zeit definiert ist, wird als die Mittlere Beschleunigung ($\bar{a}$) bezeichnet. Um es zu messen, ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) zu beobachten.
Eine g ngige Methode zur Messung der durchschnittlichen Beschleunigung besteht darin, eine Stroboskoplampe zu verwenden, die das Objekt in definierten Intervallen beleuchtet. Durch Aufnahme eines Fotos kann man die Strecke bestimmen, die das Objekt in dieser Zeit zur ckgelegt hat. Durch Berechnung von zwei aufeinanderfolgenden Geschwindigkeiten kann man ihre nderung bestimmen und mit der verstrichenen Zeit zwischen den Fotos die durchschnittliche Beschleunigung berechnen.
Die Gleichung f r die durchschnittliche Beschleunigung lautet:
Es ist wichtig zu beachten, dass die durchschnittliche Beschleunigung eine Sch tzung der tats chlichen Beschleunigung darstellt.
Das Hauptproblem besteht darin, dass, wenn sich die Beschleunigung w hrend der verstrichenen Zeit ndert, der Wert der durchschnittlichen Beschleunigung stark von der mittleren Beschleunigung abweichen kann.
Daher
Der Schl ssel ist die Beschleunigung ber einen ausreichend kurzen Zeitraum zu bestimmen, um die Variation zu minimieren.
Das Verh ltnis, in dem die Geschwindigkeits nderung im Laufe der Zeit definiert ist, wird als die Mittlere Beschleunigung ($\bar{a}$) bezeichnet. Um es zu messen, ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) zu beobachten.
Eine g ngige Methode zur Messung der durchschnittlichen Beschleunigung besteht darin, eine Stroboskoplampe zu verwenden, die das Objekt in definierten Intervallen beleuchtet. Durch Aufnahme eines Fotos kann man die Strecke bestimmen, die das Objekt in dieser Zeit zur ckgelegt hat. Durch Berechnung von zwei aufeinanderfolgenden Geschwindigkeiten kann man ihre nderung bestimmen und mit der verstrichenen Zeit zwischen den Fotos die durchschnittliche Beschleunigung berechnen.
Die Gleichung f r die durchschnittliche Beschleunigung lautet:
Es ist wichtig zu beachten, dass die durchschnittliche Beschleunigung eine Sch tzung der tats chlichen Beschleunigung darstellt.
Das Hauptproblem besteht darin, dass, wenn sich die Beschleunigung w hrend der verstrichenen Zeit ndert, der Wert der durchschnittlichen Beschleunigung stark von der mittleren Beschleunigung abweichen kann.
Daher
Der Schl ssel ist die Beschleunigung ber einen ausreichend kurzen Zeitraum zu bestimmen, um die Variation zu minimieren.
Wenn die konstante Beschleunigung ($a_0$) ist, dann ist die Mittlere Beschleunigung ($\bar{a}$) gleich dem Wert der Beschleunigung, das hei t,
In diesem Fall kann die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) berechnet werden, indem ber cksichtigt wird, dass sie mit der Differenz zwischen die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) sowie der Zeit ($t$) und der Startzeit ($t_0$) verbunden ist.
Diese Gleichung repr sentiert somit eine Gerade im Geschwindigkeits-Zeit-Raum.
Wenn die konstante Beschleunigung ($a_0$) ist, dann ist die Mittlere Beschleunigung ($\bar{a}$) gleich dem Wert der Beschleunigung, das hei t,
In diesem Fall kann die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) berechnet werden, indem ber cksichtigt wird, dass sie mit der Differenz zwischen die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) sowie der Zeit ($t$) und der Startzeit ($t_0$) verbunden ist.
Diese Gleichung repr sentiert somit eine Gerade im Geschwindigkeits-Zeit-Raum.
Im Fall von ERROR:5297.1 variiert die Geschwindigkeit ($v$) linear mit der Zeit ($t$), unter Verwendung von die Anfangsgeschwindigkeit ($v_0$) und der Startzeit ($t_0$):
Daher kann die Fl che unter dieser Linie berechnet werden, was zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$) f hrt. In Kombination mit die Ausgangsstellung ($s_0$) k nnen wir die Position ($s$) berechnen, was zu folgendem Ergebnis f hrt:
Dies entspricht der allgemeinen Form einer Parabel.
Im Fall von ERROR:5297.1 variiert die Geschwindigkeit ($v$) linear mit der Zeit ($t$), unter Verwendung von die Anfangsgeschwindigkeit ($v_0$) und der Startzeit ($t_0$):
Daher kann die Fl che unter dieser Linie berechnet werden, was zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$) f hrt. In Kombination mit die Ausgangsstellung ($s_0$) k nnen wir die Position ($s$) berechnen, was zu folgendem Ergebnis f hrt:
Dies entspricht der allgemeinen Form einer Parabel.
Im Falle einer konstanten Beschleunigung k nnen wir die Position ($s$) aus die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mit der Gleichung berechnen:
Dies erm glicht es uns, die Beziehung zwischen der w hrend der Beschleunigung/Verz gerung zur ckgelegten Strecke und der nderung der Geschwindigkeit zu bestimmen:
Im Falle einer konstanten Beschleunigung k nnen wir die Position ($s$) aus die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mit der Gleichung berechnen:
Dies erm glicht es uns, die Beziehung zwischen der w hrend der Beschleunigung/Verz gerung zur ckgelegten Strecke und der nderung der Geschwindigkeit zu bestimmen:
Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
ID:(1412, 0)