Capacitancias en serie
Storyboard 
En el caso de capacitancias en serie la diferencia de potencial aplicada genera la misma carga en todas las placas, alternándose solo el signo de estas. Con ello cada capacitancia esta bajo una diferente diferencia de potencial cuya suma es igual a la diferencia de potencial aplicada. Dado que la diferencias de potencial son iguales a la carga dividida por la capacitancia, el inverso de la capacitencia total es igual a la suma de las inversas de cada capacitancia.
ID:(1393, 0)
Suma de capacidades en serie
Imagen 
El símbolo del capacitor o condensador es el de dos placas paralelas. Si se suman en serie se les dibuja conectados uno tras el otro:
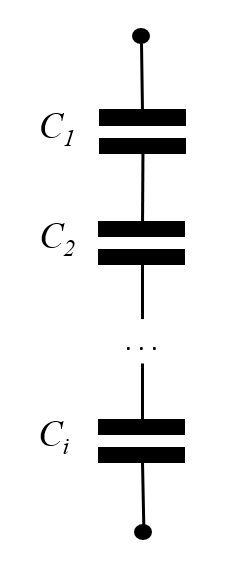
ID:(1928, 0)
Divisor de voltaje capacitivo
Imagen 
Si se conectan los condensadores en serie se puede armar un divisor de voltaje, es decir un circuito que permite obtener un voltaje menor en función de las caídas de voltaje en cada condensador:

ID:(11715, 0)
