Benützer:
Serienkapazitäten
Storyboard 
Bei einer Serienkapazität erzeugt die angelegte Potentialdifferenz auf allen Platten die gleiche Last, wobei nur deren Vorzeichen abgewechselt wird. Damit liegt jede Kapazität unter einer anderen Potentialdifferenz, deren Summe gleich der angelegten Potentialdifferenz ist. Da die Potentialdifferenzen gleich der durch die Kapazität geteilten Last sind, ist die Inverse der Gesamtkapazität gleich der Summe der Inversen jeder Kapazität.
ID:(1393, 0)
Summe der Serienkapazitäten
Bild
El símbolo del capacitor o condensador es el de dos placas paralelas. Si se suman en serie se les dibuja conectados uno tras el otro:
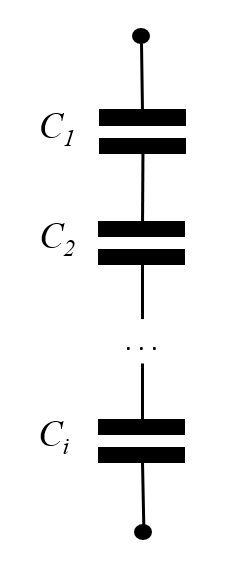
ID:(1928, 0)
Summe der Serienkapazitäten
Gleichung
Al conectar capacidades en serie en cada una de ellas ocurre una caída de potencial
$\Delta\varphi=\sum_i\Delta\varphi_i$
Los potenciales llevan a que desplazan cargas, sin embargo como inicialmente en las conexiones entre los condensadores no tienen cargas, la polarización debe ser tal que el número de cargas positivas debe ser igual a las negativas. Por ello el
$\Delta\varphi_i=\displaystyle\frac{Q}{C_i}$
Con ello el potencial total es igual a
$\Delta\varphi=\sum_i\displaystyle\frac{1}{C_i}Q$
por lo que la regla de suma de capacidades en serie será con
| $\displaystyle\frac{1}{ C_s }=\sum_i\displaystyle\frac{1}{ C_i }$ |
ID:(3217, 0)
Summe der Serienkapazitäten (2)
Gleichung
Die Summe von zwei seriellen Kapazitäten ergibt
| $\displaystyle\frac{1}{ C_{s2} }=\displaystyle\frac{1}{ C_{1s2} }+\displaystyle\frac{1}{ C_{2s2} }$ |
ID:(3869, 0)
Summe der Serienkapazitäten (3)
Gleichung
Die Summe von drei seriellen Kapazitäten ergibt
| $\displaystyle\frac{1}{ C_s }=\displaystyle\frac{1}{ C_1 }+\displaystyle\frac{1}{ C_2 }+\displaystyle\frac{1}{ C_3 }$ |
ID:(3870, 0)
Summe der Serienkapazitäten (4)
Gleichung
Die Summe von vier seriellen Kapazitäten ergibt
| $\displaystyle\frac{1}{ C_s }=\displaystyle\frac{1}{ C_1 }+\displaystyle\frac{1}{ C_2 }+\displaystyle\frac{1}{ C_3 }+\displaystyle\frac{1}{ C_4 }$ |
ID:(3871, 0)
Kapazitiver Spannungsteiler
Bild
Si se conectan los condensadores en serie se puede armar un divisor de voltaje, es decir un circuito que permite obtener un voltaje menor en función de las caídas de voltaje en cada condensador:
ID:(11715, 0)
Kapazitiver Spannungsteiler, Spannung 1
Gleichung
Como el potencial total debe ser
$\Delta\varphi = \Delta\varphi_1+\Delta\varphi_2$
y las cargas ser iguales
$Q = C_1\Delta\varphi_1=C_2\Delta\varphi_2$
se tiene que con
| $ \Delta\varphi_1 =\displaystyle\frac{ C_1 }{ C_1 + C_2 } \Delta\varphi $ |
ID:(11716, 0)
Kapazitiver Spannungsteiler, Spannung 2
Gleichung
Como el potencial total debe ser
$\Delta\varphi = \Delta\varphi_1+\Delta\varphi_2$
y las cargas ser iguales
$Q = C_1\Delta\varphi_1=C_2\Delta\varphi_2$
se tiene que con
| $ \Delta\varphi_2 =\displaystyle\frac{ C_2 }{ C_1 + C_2 } \Delta\varphi $ |
ID:(11717, 0)