Ley de Ohm
Storyboard 
Si se aplica un campo a una carga se obtiene una fuerza. Dicha fuerza aplicada a lo largo de un camino lleva a una energía potencial. Si se expresa con un campo eléctrico se obtiene la energía potencial por carga que denominamos potencial eléctrico. El potencial eléctrico genera desplazamiento de cargas lo que implica que existe un flujo que denominamos corriente eléctrica. Su magnitud depende del potencial eléctrico y de la resistencia que presenta el material en que están los electrones que denominaremos conductor. La ley resultante es la llamada ley de Ohm.
ID:(815, 0)
Corriente por un conductor
Definición 
En resumen la aplicación de una diferencia de potencial entre los dos extremos del conductor
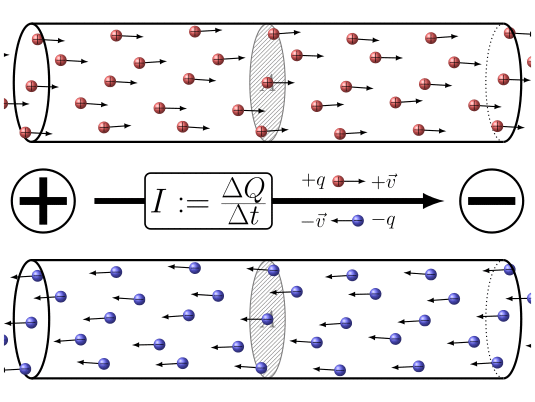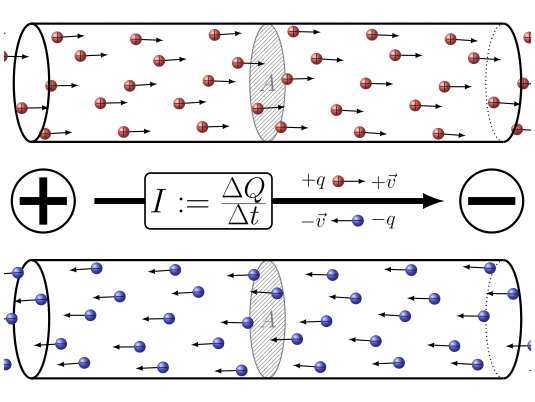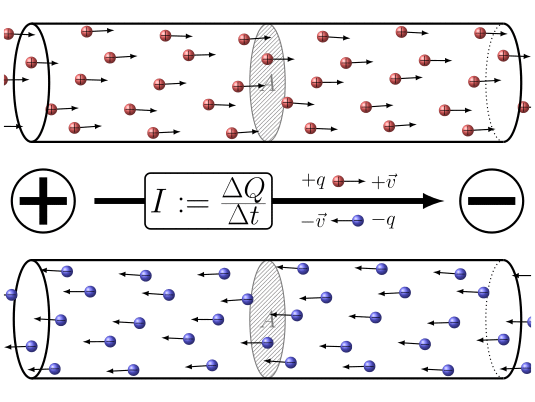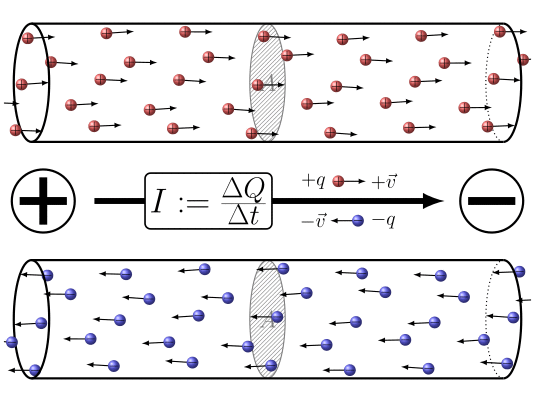
ID:(7860, 0)
Resistencia y calor
Imagen 
El calor hace que los átomos oscila con una mayor amplitud dificultando el avance de los electrones:
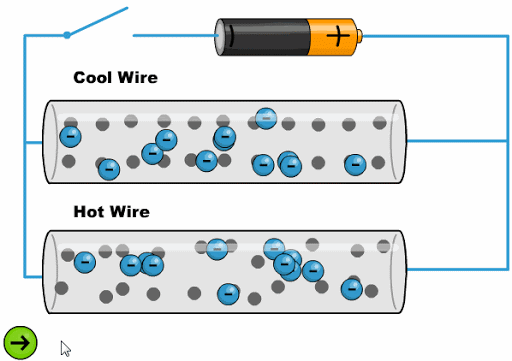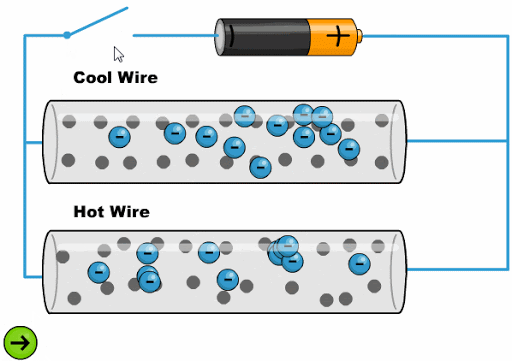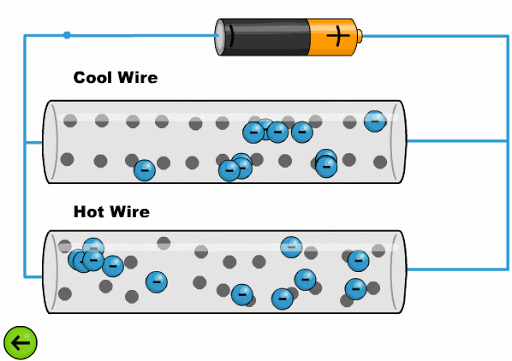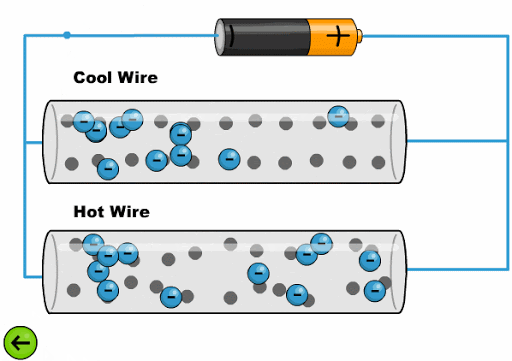
ID:(11761, 0)
Ley de Ohm
Storyboard 
Cuando se aplica un campo a una carga, se genera una fuerza. Esta fuerza, al actuar a lo largo de un camino, da lugar a una energía potencial. Si esta energía potencial se expresa en términos de un campo eléctrico, obtenemos la energía potencial por unidad de carga, conocida como potencial eléctrico. El potencial eléctrico induce el desplazamiento de cargas, generando un flujo denominado corriente eléctrica. La magnitud de esta corriente depende tanto del potencial eléctrico aplicado como de la resistencia que presenta el material a través del cual se desplazan las cargas, comúnmente conocido como conductor. La relación resultante entre el potencial eléctrico, la corriente y la resistencia está descrita por la conocida ley de Ohm.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En resumen la aplicaci n de una diferencia de potencial entre los dos extremos del conductor
El calor hace que los tomos oscila con una mayor amplitud dificultando el avance de los electrones:
Cuando las cargas el ctricas se desplazan, es posible definir una cantidad la elemento de carga ($\Delta Q$), que representa el flujo de carga que atraviesa una secci n en un intervalo de tiempo el tiempo transcurrido ($\Delta t$). Esta cantidad est relacionada con una corriente ($I$) y se define mediante la siguiente expresi n:
El campo eléctrico ($E$) es generado por la diferencia de potencial ($\Delta\varphi$) entre los dos electrodos, separados por una distancia de un largo del conductor ($L$). Este valor se puede calcular mediante la siguiente expresi n:
La velocidad máxima ($v_{max}$) se alcanza, en promedio, cuando el electrón es acelerado con la aceleración de cargas en conductor ($a$) durante un intervalo de el tiempo entre choques ($\tau$), lo que resulta en:
El campo eléctrico ($E$) generates, together with la carga del electrón ($e$), a force that, through la masa del electrón ($m_e$), results in la aceleración de cargas en conductor ($a$). This relationship is expressed as follows:
En un tiempo entre choques ($\tau$), el electr n es acelerado por el campo eléctrico ($E$), en combinaci n con la carga del electrón ($e$) y la masa del electrón ($m_e$), hasta alcanzar la velocidad máxima ($v_{max}$). Este proceso se describe mediante la siguiente relaci n:
Dado que el electrón se acelera de forma uniforme, su velocidad aumenta linealmente con el tiempo hasta alcanzar la velocidad máxima ($v_{max}$). Por lo tanto, la velocidad media la velocidad media de las cargas ($\bar{v}$) es:
La corriente ($I$) se puede calcular considerando los electrones con una concentración de cargas ($c$) y la carga del electrón ($e$), que se mueven con una velocidad media de las cargas ($\bar{v}$) a trav s de ERROR:5475,1. Esta relaci n se expresa como:
La corriente ($I$) se puede calcular a partir de el campo eléctrico ($E$), en combinación con la carga del electrón ($e$), la concentración de cargas ($c$), la masa del electrón ($m_e$), el tiempo entre choques ($\tau$) y ERROR:5475, utilizando la siguiente relaci n:
Si la corriente ($I$) se expresa utilizando la diferencia de potencial ($\Delta\varphi$) en lugar de el campo eléctrico ($E$), se obtiene la ecuaci n microscópica de Ohm. Esta ecuaci n se formula con la carga del electrón ($e$), la concentración de cargas ($c$), la masa del electrón ($m_e$), el tiempo entre choques ($\tau$), ERROR:5475 y el largo del conductor ($L$), a trav s de la siguiente relaci n:
A partir de la ecuaci n microsc pica de Ohm, se identifica un factor caracter stico del material del conductor. Esto permite definir la resistividad ($\rho_e$) en funci n de la carga del electrón ($e$), la concentración de cargas ($c$), la masa del electrón ($m_e$) y el tiempo entre choques ($\tau$), utilizando la siguiente relaci n:
Utilizando la resistividad ($\rho_e$) junto con los par metros geom tricos de el largo del conductor ($L$) y ERROR:5475, se puede definir la resistencia ($R$) a trav s de la siguiente relaci n:
La ley de Ohm tradicional establece una relaci n entre la diferencia de potencial ($\Delta\varphi$) y la corriente ($I$) a trav s de la resistencia ($R$), utilizando la siguiente expresi n:
ID:(815, 0)
