Usuario:


Dieléctricos dentro de capacitancias
Storyboard

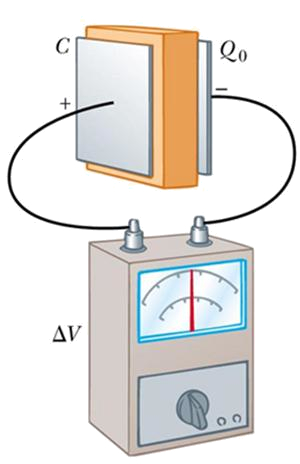
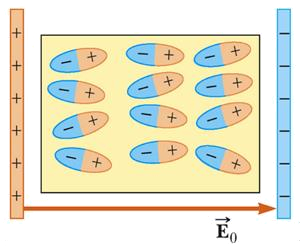
Tanto para mantener separadas las placas de los capacitores como para aumentar su capacidad se colocan dieléctricos entre ambas placas. Al cargarse le capacitor se genera un campo eléctrico entre las placas que polariza las moléculas del dieléctrico. Esto actúa como un sistema de múltiples capacitores conectados en serie lo que es equivalente a aumentar la sección y con ello la capacidad.

>Modelo

ID:(1395, 0)


Descarga de una capacidad
Definición

ID:(1926, 0)


Dieléctricos dentro de capacitancias
Descripción

Tanto para mantener separadas las placas de los capacitores como para aumentar su capacidad se colocan dieléctricos entre ambas placas. Al cargarse le capacitor se genera un campo eléctrico entre las placas que polariza las moléculas del dieléctrico. Esto actúa como un sistema de múltiples capacitores conectados en serie lo que es equivalente a aumentar la sección y con ello la capacidad.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$C$
C
Capacidad del capacitor
F
$\epsilon$
epsilon
Constante dieléctrica
-
$d$
d
Distancia entre placas
m
$S$
S
Superficie de placas
m^2

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

ID:(1395, 0)