Capacitores
Storyboard 
Los capacitores son elementos que permiten en circuitos almacenar dinamicamente carga. Se polrizan y pueden descargar en función de como se les aplique potenciales que cargan o descargan cargas en sus placas.
ID:(1579, 0)
Ejemplo de capacitores
Definición 
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayoría tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:

ID:(11703, 0)
Unidades de la capacidad
Imagen 
La capacidad se define como la relación entre la carga y el potencial eléctrico:
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
El primero se mide en Coulomb, el segundo en Volt. La división de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
ID:(11714, 0)
Diagrama de un circuito
Nota 
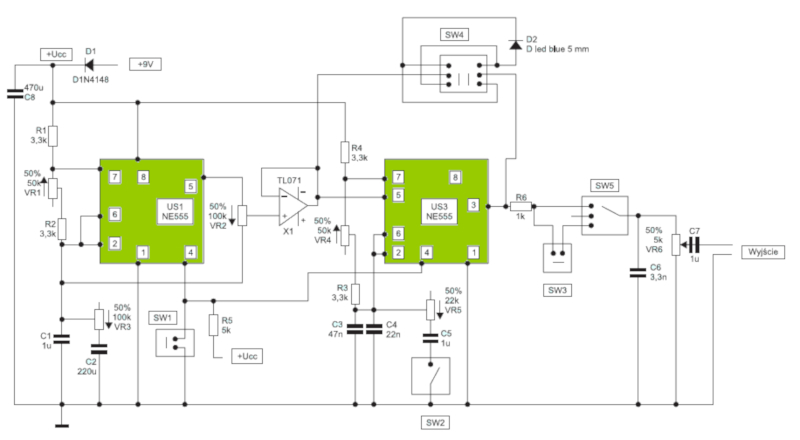
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con números)
ID:(11704, 0)
Ejemplo de circuito impreso
Cita 
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con métodos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• procesadores (cajas rectangulares con números)

ID:(11705, 0)
Placas paralelas, geometría
Ejercicio 
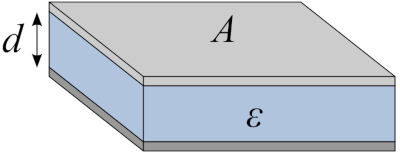
Dos placas paralelas con un dieléctrico entre ellos forman un condensador:
ID:(11706, 0)
Cilindros concentricos, geometría
Ecuación 
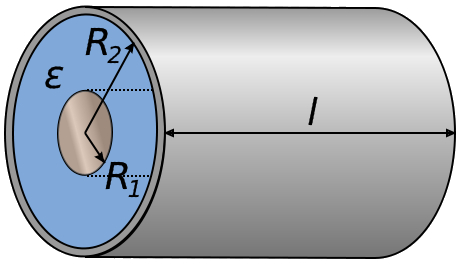
Dos cilindros concentricos con un dieléctrico entre ellos forman un condensador:
ID:(11707, 0)
Esferas concentricas, geometría
Script 
Dos esferas concentricas con un dieléctrico entre ellas forman un condensador:

ID:(11709, 0)
Alambres paralelos, geometría
Variable 
Dos alambres pueden formar entre ellos un condensador:

Esto puede ser también involuntario.
ID:(11708, 0)
Capacitores
Storyboard 
Los capacitores son elementos que permiten en circuitos almacenar dinamicamente carga. Se polrizan y pueden descargar en función de como se les aplique potenciales que cargan o descargan cargas en sus placas.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Al conectar capacidades en paralelo ca da de potencial
$Q=\displaystyle\sum_i Q_i$
Si ahora se aplica la relaci n de las capacidades para cada una de estas se tendr para potenciales iguales que
$\Delta\varphi=\displaystyle\frac{Q_i}{C_i}$
Con ello la carga total es igual a
$Q=\displaystyle\sum_i C_i\Delta\varphi$
por lo que la regla de suma de capacidades en paralelo ser con
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayor a tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:
La capacidad se define como la relaci n entre la carga y el potencial el ctrico:
El primero se mide en Coulomb, el segundo en Volt. La divisi n de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con n meros)
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con m todos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• procesadores (cajas rectangulares con n meros)
Dos placas paralelas con un diel ctrico entre ellos forman un condensador:
La capacidad de un capacitor formado por dos placas paralelas es con
Dos cilindros concentricos con un diel ctrico entre ellos forman un condensador:
La capacidad de un capacitor formado por dos cilindros concentricos es con
Dos esferas concentricas con un diel ctrico entre ellas forman un condensador:
La capacidad de un capacitor formado por dos esferas concentricas es con
Dos alambres pueden formar entre ellos un condensador:
Esto puede ser tambi n involuntario.
La capacidad de un capacitor formado por dos alambres es con
ID:(1579, 0)
