Ohmsches Gesetz
Storyboard 
Wenn ein Feld an eine Last angelegt wird, wird eine Kraft erhalten. Eine solche Kraft, die entlang eines Pfades ausgeübt wird, führt zu potentieller Energie. Wird es durch ein elektrisches Feld ausgedrückt, erhält man die potentielle Energie pro Ladung, die wir elektrisches Potential nennen. Das elektrische Potential erzeugt eine Verschiebung von Ladungen, was impliziert, dass es einen Fluss gibt, den wir elektrischen Strom nennen. Ihre Größe hängt von dem elektrischen Potential und dem Widerstand des Materials ab, in dem sich die Elektronen befinden, die wir den Leiter nennen werden. Das resultierende Gesetz ist das sogenannte Ohmsche Gesetz.
ID:(815, 0)
Strom durch einen Leiter
Definition 
Zusammenfassend lässt sich sagen, dass durch Anlegen einer Potentialdifferenz zwischen den beiden Enden des Leiters
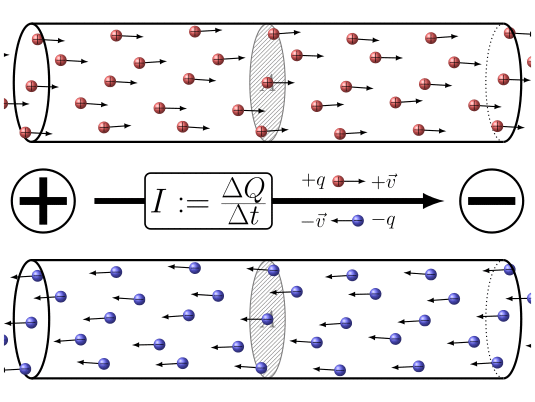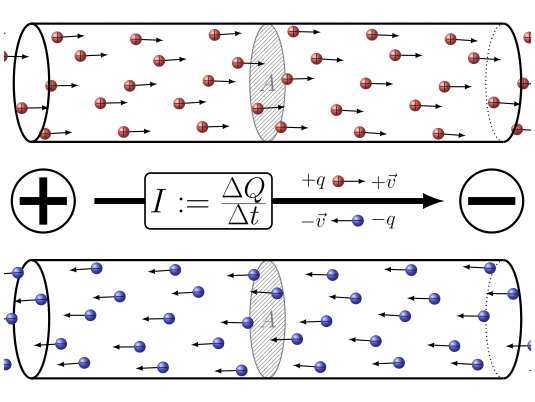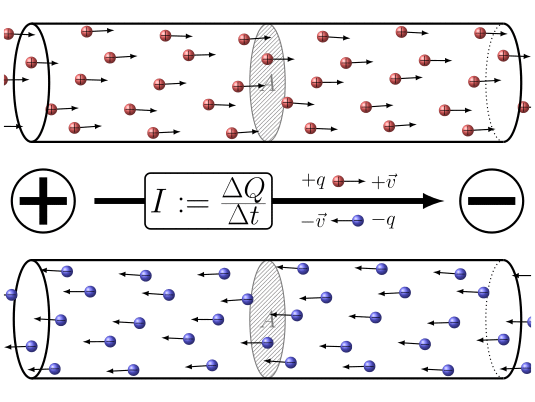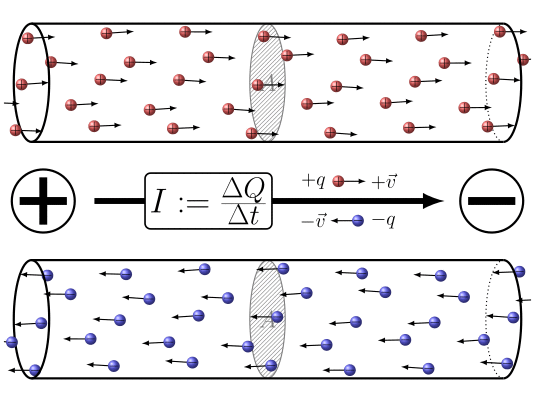
ID:(7860, 0)
Widerstand und Hitze
Bild 
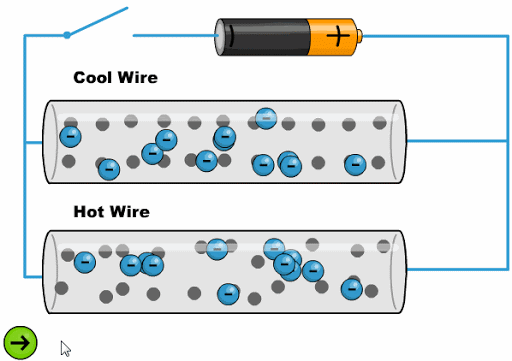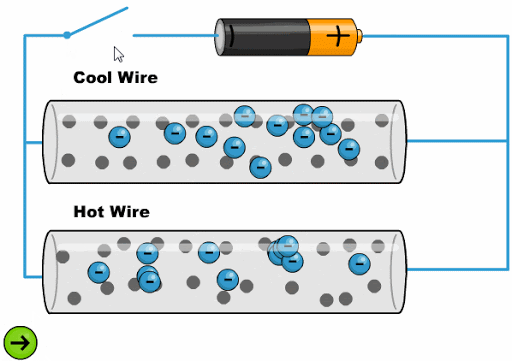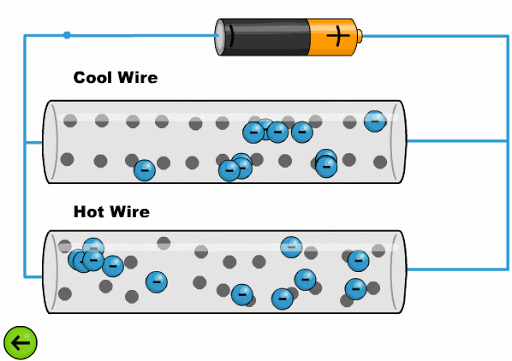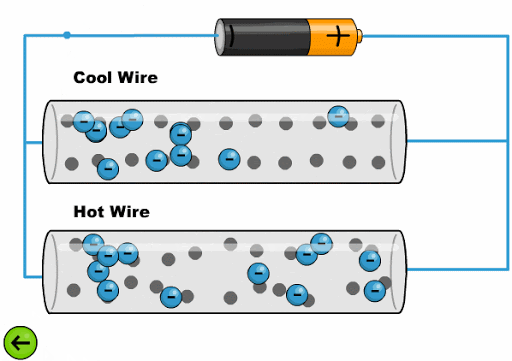
Die Hitze lässt die Atome mit einer größeren Amplitude schwingen, was es den Elektronen erschwert, voranzukommen:
ID:(11761, 0)
Ohmsches Gesetz
Storyboard 
Wenn ein Feld auf eine Ladung angewendet wird, entsteht eine Kraft. Diese Kraft führt, wenn sie entlang eines Weges wirkt, zu einer potenziellen Energie. Wenn diese potenzielle Energie in Bezug auf ein elektrisches Feld ausgedrückt wird, erhält man die potenzielle Energie pro Ladungseinheit, die als elektrisches Potenzial bekannt ist. Das elektrische Potenzial bewirkt die Bewegung von Ladungen, was einen Fluss erzeugt, der als elektrischer Strom bezeichnet wird. Die Größe dieses Stroms hängt sowohl vom angelegten elektrischen Potenzial als auch vom Widerstand des Materials ab, durch das sich die Ladungen bewegen, das üblicherweise als Leiter bezeichnet wird. Die daraus resultierende Beziehung zwischen elektrischem Potenzial, Strom und Widerstand wird durch das bekannte Ohmsche Gesetz beschrieben.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Zusammenfassend l sst sich sagen, dass durch Anlegen einer Potentialdifferenz zwischen den beiden Enden des Leiters
Die Hitze l sst die Atome mit einer gr eren Amplitude schwingen, was es den Elektronen erschwert, voranzukommen:
Wenn sich elektrische Ladungen bewegen, kann eine Gr e die Ladungelement ($\Delta Q$) definiert werden, die die Menge an Ladung darstellt, die in einem Zeitintervall der Abgelaufene Zeit ($\Delta t$) durch einen Querschnitt flie t. Diese Gr e steht in Zusammenhang mit eine Strom ($I$) und wird durch die folgende Gleichung definiert:
Der Elektrisches Feld ($E$) wird durch die Potentialdifferenz ($\Delta\varphi$) zwischen zwei Elektroden erzeugt, die durch eine Distanz von ein Leitungslänge ($L$) getrennt sind. Dieser Wert kann mit der folgenden Gleichung berechnet werden:
Die Höchstgeschwindigkeit ($v_{max}$) wird im Durchschnitt erreicht, wenn das Elektron mit die Beschleunigung der Ladung in der Leitung ($a$) während des Zeitintervalls der Zeit zwischen Kollisionen ($\tau$) beschleunigt wird, was ergibt:
Der Elektrisches Feld ($E$) erzeugt zusammen mit die Elektronenladung ($e$) eine Kraft, die durch die Masse des Elektrons ($m_e$) in die Beschleunigung der Ladung in der Leitung ($a$) resultiert. Diese Beziehung kann wie folgt ausgedr ckt werden:
In ein Zeit zwischen Kollisionen ($\tau$) wird das Elektron durch der Elektrisches Feld ($E$) in Kombination mit die Elektronenladung ($e$) und die Masse des Elektrons ($m_e$) beschleunigt, bis es die Höchstgeschwindigkeit ($v_{max}$) erreicht. Dieser Prozess wird durch die folgende Beziehung beschrieben:
Da das Elektron gleichmäßig beschleunigt wird, steigt seine Geschwindigkeit linear mit der Zeit, bis es die Höchstgeschwindigkeit ($v_{max}$) erreicht. Daher ist die mittlere Geschwindigkeit die Durchschnittliche Ladungsgeschwindigkeit ($\bar{v}$):
Die Strom ($I$) kann berechnet werden, indem Elektronen mit eine Ladungs Konzentration ($c$) und die Elektronenladung ($e$) betrachtet werden, die sich mit eine Durchschnittliche Ladungsgeschwindigkeit ($\bar{v}$) durch eine Abschnitt der Leiter ($S$) bewegen. Diese Beziehung wird wie folgt ausgedr ckt:
Die Strom ($I$) kann aus der Elektrisches Feld ($E$) in Kombination mit die Elektronenladung ($e$), die Ladungs Konzentration ($c$), die Masse des Elektrons ($m_e$), der Zeit zwischen Kollisionen ($\tau$) und die Abschnitt der Leiter ($S$) berechnet werden, mithilfe der folgenden Beziehung:
Wenn die Strom ($I$) unter Verwendung von die Potentialdifferenz ($\Delta\varphi$) anstelle von der Elektrisches Feld ($E$) ausgedr ckt wird, ergibt sich die mikroskopische Form des Ohmschen Gesetzes. Diese Gleichung umfasst die Elektronenladung ($e$), die Ladungs Konzentration ($c$), die Masse des Elektrons ($m_e$), der Zeit zwischen Kollisionen ($\tau$), die Abschnitt der Leiter ($S$) und der Leitungslänge ($L$) und wird durch die folgende Beziehung beschrieben:
Aus der mikroskopischen Form des Ohm'schen Gesetzes l sst sich ein Faktor erkennen, der spezifisch f r das Material des Leiters ist. Dies erm glicht die Definition von die Spezifischer Widerstand ($\rho_e$) in Abh ngigkeit von die Elektronenladung ($e$), die Ladungs Konzentration ($c$), die Masse des Elektrons ($m_e$) und der Zeit zwischen Kollisionen ($\tau$), mithilfe der folgenden Beziehung:
Mit die Spezifischer Widerstand ($\rho_e$) und den geometrischen Parametern der Leitungslänge ($L$) und die Abschnitt der Leiter ($S$) kann die Widerstand ($R$) durch die folgende Beziehung definiert werden:
Das traditionelle Ohmsche Gesetz stellt eine Beziehung zwischen die Potentialdifferenz ($\Delta\varphi$) und die Strom ($I$) ber die Widerstand ($R$) her, unter Verwendung der folgenden Gleichung:
ID:(815, 0)
