Ohm's Law
Storyboard 
If a field is applied to a load, a force is obtained. Such force applied along a path leads to potential energy. If it is expressed with an electric field, the potential energy per charge that we call electrical potential is obtained. The electric potential generates displacement of charges which implies that there is a flow that we call electric current. Its magnitude depends on the electrical potential and the resistance that the material in which the electrons that we will call the conductor are. The resulting law is the so-called Ohm's law.
ID:(815, 0)
Current by a conductor
Definition 
In summary, the application of a potential difference between the two ends of the
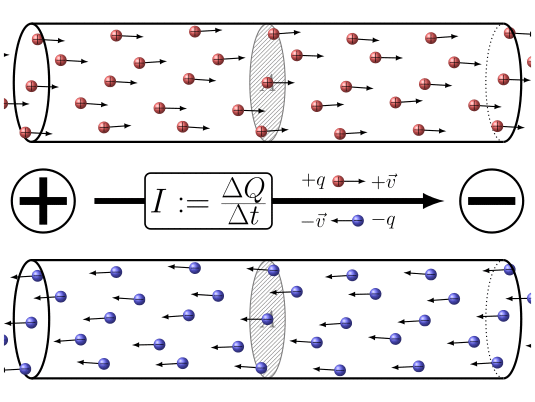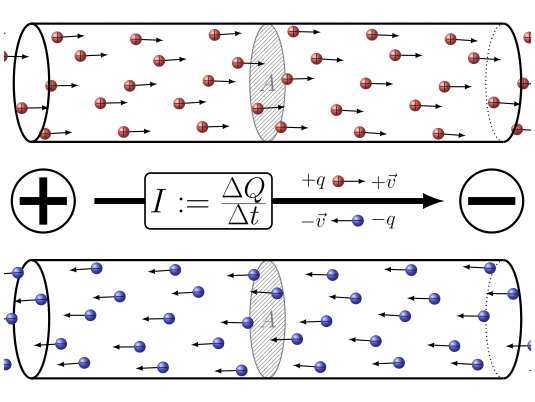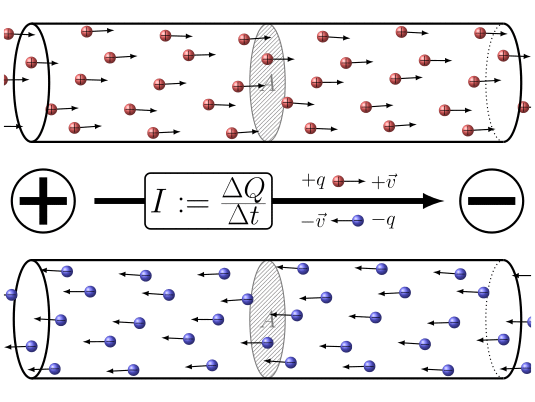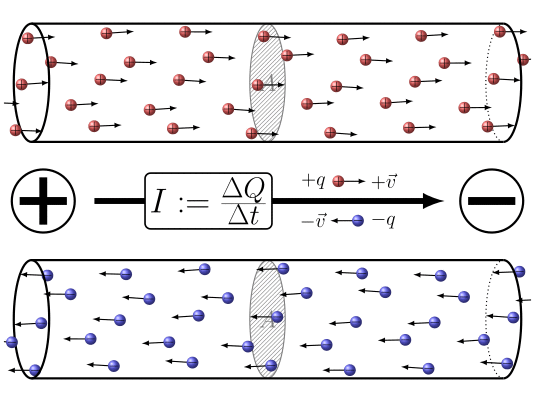
ID:(7860, 0)
Resistance and heat
Image 
The heat makes the atoms oscillate with a greater amplitude, making it difficult for the electrons to advance:
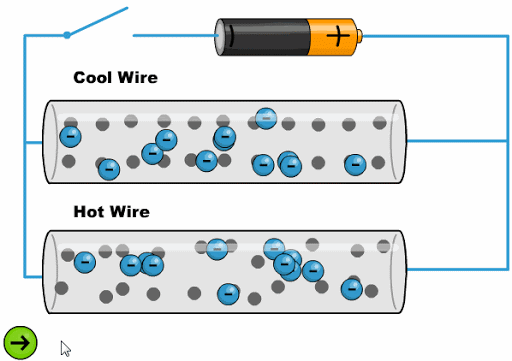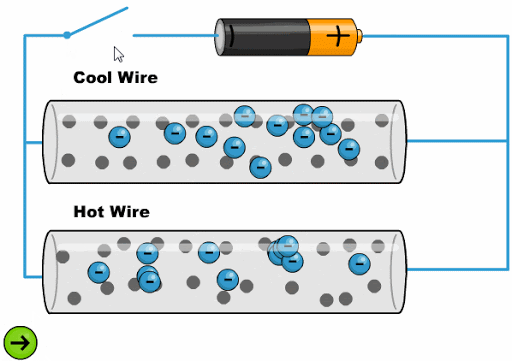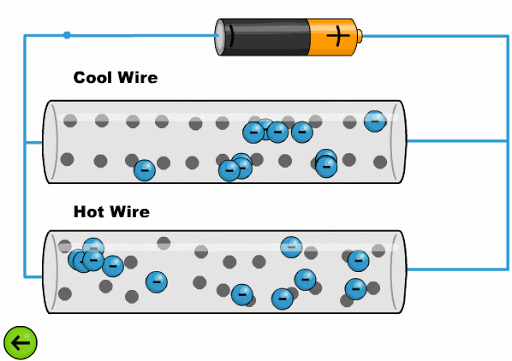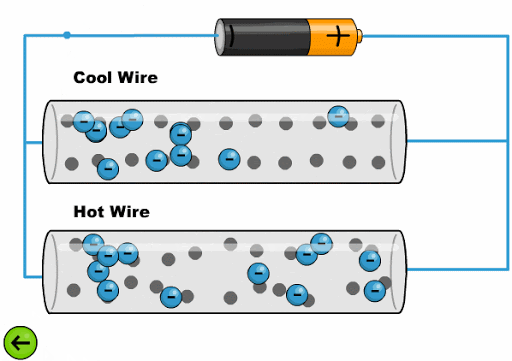
ID:(11761, 0)
Ohm's Law
Storyboard 
When a field is applied to a charge, it generates a force. This force, when acting along a path, gives rise to potential energy. If this potential energy is expressed in terms of an electric field, it becomes the potential energy per unit charge, known as electric potential. The electric potential induces the movement of charges, creating a flow called electric current. The magnitude of this current depends on both the applied electric potential and the resistance of the material through which the charges move, commonly referred to as the conductor. The resulting relationship between electric potential, current, and resistance is described by the well-known Ohm's law.
Variables
Calculations
Calculations
Equations
Examples
In summary, the application of a potential difference between the two ends of the
The heat makes the atoms oscillate with a greater amplitude, making it difficult for the electrons to advance:
When electric charges move, it is possible to define a quantity the load element ($\Delta Q$), representing the amount of charge passing through a section over a time interval the time elapsed ($\Delta t$). This quantity is related to a current ($I$) and is defined by the following expression:
The electric eield ($E$) is generated by the potential difference ($\Delta\varphi$) between two electrodes, separated by a distance of a conductor length ($L$). This value can be calculated using the following expression:
The maximum Speed ($v_{max}$) is reached on average when the electron accelerates with the acceleration of charge in the conductor ($a$) during the time interval the time between collisions ($\tau$), resulting in:
The electric eield ($E$), together with the electron Charge ($e$), generates a force that, through the mass of the electron ($m_e$), results in the acceleration of charge in the conductor ($a$). This relationship can be expressed as:
In a time between collisions ($\tau$), the electron is accelerated by the electric eield ($E$), in combination with the electron Charge ($e$) and the mass of the electron ($m_e$), until it reaches the maximum Speed ($v_{max}$). This process is described by the following relationship:
Since the electron accelerates uniformly, its velocity increases linearly over time until it reaches the maximum Speed ($v_{max}$). Therefore, the average velocity the average speed of charges ($\bar{v}$) is:
The current ($I$) can be calculated by considering electrons with a charge concentration ($c$) and the electron Charge ($e$), moving at a average speed of charges ($\bar{v}$) through a section of Conductors ($S$). This relationship is expressed as:
The current ($I$) can be calculated from the electric eield ($E$), in combination with the electron Charge ($e$), the charge concentration ($c$), the mass of the electron ($m_e$), the time between collisions ($\tau$), and the section of Conductors ($S$), using the following relationship:
If the current ($I$) is expressed using the potential difference ($\Delta\varphi$) instead of the electric eield ($E$), the microscopic form of Ohm's law is obtained. This equation involves the electron Charge ($e$), the charge concentration ($c$), the mass of the electron ($m_e$), the time between collisions ($\tau$), the section of Conductors ($S$), and the conductor length ($L$), through the following relationship:
From the microscopic form of Ohm's law, a factor specific to the material of the conductor can be identified. This allows the resistivity ($\rho_e$) to be defined in terms of the electron Charge ($e$), the charge concentration ($c$), the mass of the electron ($m_e$), and the time between collisions ($\tau$), using the following relationship:
Using the resistivity ($\rho_e$) along with the geometric parameters the conductor length ($L$) and the section of Conductors ($S$), the resistance ($R$) can be defined through the following relationship:
Traditional Ohm's law establishes a relationship between the potential difference ($\Delta\varphi$) and the current ($I$) through the resistance ($R$), using the following expression:
ID:(815, 0)
