Benützer:
Momentane Winkelbeschleunigung
Storyboard 
Um zu beschreiben, wie sich die Winkelgeschwindigkeit im Laufe der Zeit entwickelt, muss man ihre Variation im Verhältnis zur Zeit betrachten.
Die Beziehung zur Veränderung der Winkelgeschwindigkeit entspricht der Winkelverschiebung über die verstrichene Zeit, die, wenn sie durch diese Zeit geteilt wird, die Winkelbeschleunigung ergibt.
Für ein infinitesimal kleines Zeitintervall entspricht die Winkelbeschleunigung der momentanen Winkelbeschleunigung.
ID:(1452, 0)
Momentane Winkelbeschleunigung
Storyboard
Um zu beschreiben, wie sich die Winkelgeschwindigkeit im Laufe der Zeit entwickelt, muss man ihre Variation im Verhältnis zur Zeit betrachten. Die Beziehung zur Veränderung der Winkelgeschwindigkeit entspricht der Winkelverschiebung über die verstrichene Zeit, die, wenn sie durch diese Zeit geteilt wird, die Winkelbeschleunigung ergibt. Für ein infinitesimal kleines Zeitintervall entspricht die Winkelbeschleunigung der momentanen Winkelbeschleunigung.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Angesichts der Tatsache, dass die Tangentialbeschleunigung
ist, und wenn der Einheitsvektor der Achse $\hat{n}$ und der radiale Einheitsvektor $\hat{r}$ ist, kann der Tangentialvektor durch das Kreuzprodukt berechnet werden:
$\hat{t} = \hat{n} \times \hat{r}$
Folglich, unter Ber cksichtigung dessen, dass
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
und
$\vec{\alpha} = \alpha \hat{n}$
,
k nnen wir ableiten, dass
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
was sich bersetzen l sst in
Beispiele
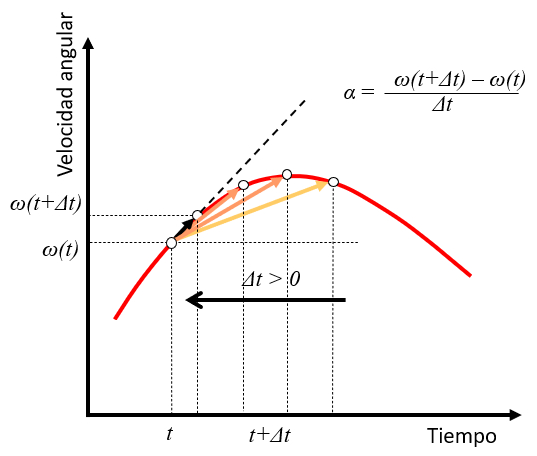
Wenn eine Zeitspanne $t$ mit einer Winkelgeschwindigkeit $\omega(t)$ verstrichen ist und ein Punkt zu einem zuk nftigen Zeitpunkt $t+\Delta t$ mit einer Winkelgeschwindigkeit $\omega(t+\Delta t)$ beobachtet wird, kann die Winkelbeschleunigung als die Variation
$\omega(t+\Delta t)-\omega(t)$
ber die Zeit $\Delta t$ abgesch tzt werden:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ kleiner wird, nimmt die Beschleunigung die Rolle der Tangente an der Geschwindigkeitskurve zu diesem Zeitpunkt ein:
Dies verallgemeinert, was bereits f r den Fall konstanter Winkelbeschleunigung gesehen wurde.
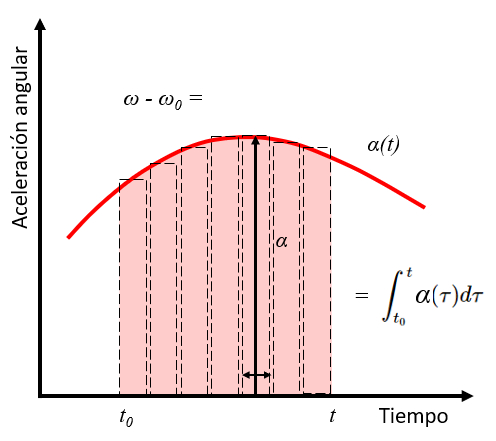
Das Integral einer Funktion entspricht der Fl che unter der Kurve, die die Funktion definiert. Daher entspricht das Integral der Winkelbeschleunigung zwischen den Zeiten $t_0$ und $t$ der nderung der Winkelgeschwindigkeit zwischen der anf nglichen Winkelgeschwindigkeit $\omega_0$ und $\omega$.
Unter Verwendung von
Dies wird im folgenden Diagramm dargestellt:
Die Ausrichtung der Tangentialbeschleunigung kann mithilfe der Rechten-Hand-Regel ermittelt werden, indem die Finger in Richtung der Achse zeigen und dann in Richtung des Radius gedreht werden:
hnlich wie bei der translatorischen Beschleunigung gibt es das Konzept der Momentanen Winkelbeschleunigung, die die Winkelbeschleunigung mit
ist, die zu einem bestimmten Zeitpunkt existiert. Dies wird in der N herung von sehr kleinen Zeitintervallen $(\Delta t\rightarrow 0)$ berechnet, was bedeutet
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
wobei
Wenn wir die Definition der Winkelgeschwindigkeit mit Hilfe von
Das bedeutet, dass f r ein Zeitintervall $dt$ der zur ckgelegte Winkel gegeben ist durch:
$d\omega = \alpha dt$
Wenn wir $N$ Intervalle $dt_i$ mit den entsprechenden Winkelgeschwindigkeiten $\alpha_i$ betrachten, ergibt sich der gesamte zur ckgelegte Winkel zu:
$\omega - \omega_0 = \sum_i \alpha_i dt_i$
Unter Ber cksichtigung der Winkelgeschwindigkeit-Zeit-Kurve entsprechen die Elemente $\alpha_i dt_i$ Rechtecken mit einer H he von $\alpha_i$ und einer Breite von $dt_i$. Die Summe entspricht somit der Fl che unter der Winkelgeschwindigkeit-Zeit-Kurve. Daher kann die Summe als Integral unter Verwendung von
Im Allgemeinen muss die Beschleunigung als ein dreidimensionales Gebilde verstanden werden, das hei t, als Vektor. Ihre Geschwindigkeit muss daher durch einen Vektor, den Drehgeschwindigkeitsvektor $\vec{\omega}$, beschrieben werden, f r den eine Komponentenbeschleunigung mit
definiert werden kann, womit die Beschleunigung verallgemeinert werden kann:
Die Integration der differentiellen Definition, d. h. infinitesimaler zeitlicher Variationen, in Bezug auf die Gleichung
Wir k nnen eine Integration zwischen der Zeit $t_0$ und $t$ der Beschleunigung $a(\tau)$ durchf hren, um die Geschwindigkeit $v(t)$ zu erhalten, wenn die Anfangsgeschwindigkeit $v_0$ gegeben ist, unter Verwendung der Gleichung:
Die Winkelbeschleunigung wird als Vektor in Richtung der Rotationsachse dargestellt. Da der Rotationsradius und die Winkelbeschleunigung orthogonal zur Tangentialbeschleunigung sind, ergibt sich:
Diese Beziehung kann als Kreuzprodukt aus Winkelbeschleunigung und Radius ausgedr ckt werden, dargestellt als:
ID:(1452, 0)
