Momentane Winkelgeschwindigkeit
Storyboard 
Die durchschnittliche Winkelgeschwindigkeit wird definiert, indem der über einen Zeitintervall durchlaufene Winkel berücksichtigt wird, ohne mögliche Schwankungen der Winkelgeschwindigkeit zu beachten.Um die Winkelgeschwindigkeit zu einem bestimmten Zeitpunkt zu bestimmen, ist es erforderlich, ein extrem kleines Zeitintervall zu betrachten, sodass die Winkelgeschwindigkeit in diesem Zeitraum keine signifikanten Änderungen aufweist.Daher wird die momentane Winkelgeschwindigkeit durch Berechnung der durchschnittlichen Winkelgeschwindigkeit im Grenzwert eines gegen Null strebenden Zeitintervalls erhalten. Mathematisch betrachtet entspricht dies der Ableitung des Winkels nach der Zeit und repräsentiert die Steigung der Winkel-Zeit-Kurve.
ID:(1447, 0)
Winkelgeschwindigkeit als Ableitung
Konzept 
Wenn wir zu einem Zeitpunkt $t$ einen Winkel $\theta(t)$ betrachten und zu einem zukünftigen Zeitpunkt $t+\Delta t$ einen Winkel $\theta(t+\Delta t)$, können wir die Geschwindigkeit als den zurückgelegten Winkel
$\theta(t+\Delta t)-\theta(t)$
in der Zeit $\Delta t$ schätzen.
$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ verringert wird, übernimmt die Winkelgeschwindigkeit die Rolle der Tangente zur Positions-Kurve zu diesem Zeitpunkt:
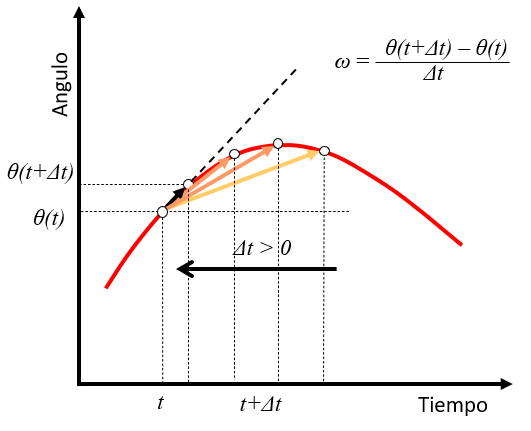
Dies verallgemeinert, was bereits für den Fall konstanter Winkelgeschwindigkeit gesehen wurde.
ID:(11407, 0)
Zurückgelegter Segmentflächenwinkel
Beschreibung 
Wenn wir feststellen, dass die Winkelgeschwindigkeit $\omega$ gleich dem Winkel $\Delta\theta$ multipliziert mit der Zeit $\Delta t$ ist, können wir sagen, dass die Verschiebung
$\Delta\theta = \omega\Delta t$
ist. Da das Produkt $\omega\Delta t$ den Bereich unter der Kurve der Winkelgeschwindigkeit in Abhängigkeit von der Zeit repräsentiert und dieser Bereich gleichzeitig der zurückgelegten Verschiebung entspricht:

ID:(11417, 0)
Winkel als Integral der Winkelgeschwindigkeit
Beschreibung 
Das Integral einer Funktion entspricht der Fläche unter der Kurve, die die Funktion definiert. Daher entspricht das Integral der Geschwindigkeit zwischen den Zeiten $t_0$ und $t$ dem durchlaufenden Winkel zwischen der Ausgangsposition $\theta_0$ und $\theta$.
Dies kann mathematisch wie folgt ausgedrückt werden:
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
Diese Beziehung wird grafisch unten dargestellt:

Diese Formel ist nützlich, um den durchlaufenden Winkel eines Objekts in Situationen zu berechnen, in denen die Geschwindigkeitsfunktion bekannt ist. Das Integral der Geschwindigkeitsfunktion liefert ein Maß für die Gesamtverschiebung des Objekts zwischen den beiden Zeiten $t_0$ und $t$, das zur Berechnung des durchlaufenden Winkels des Objekts verwendet werden kann, indem man die Verschiebung durch den Radius des Kreises teilt. Dieses Konzept ist besonders nützlich in Physik- und Ingenieur-Anwendungen, in denen Rotationsbewegungen beteiligt sind.
ID:(11409, 0)
Tangentialgeschwindigkeit, rechte Hand Regel
Bild 
Die Orientierung der Tangentialgeschwindigkeit kann mit der Rechten-Hand-Regel bestimmt werden. Wenn die Finger in Richtung der Rotationsachse zeigen und dann in Richtung des Positionsvektors (Radius) gebogen werden, zeigt der Daumen in Richtung der Tangentialgeschwindigkeit:

ID:(11599, 0)
Tangentialgeschwindigkeit
Beschreibung 
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung würde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausführt, die dem Radius mal der Winkelgeschwindigkeit entspricht:

Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
ID:(310, 0)
Momentane Winkelgeschwindigkeit
Modell 
Die durchschnittliche Winkelgeschwindigkeit wird definiert, indem der über einen Zeitintervall durchlaufene Winkel berücksichtigt wird, ohne mögliche Schwankungen der Winkelgeschwindigkeit zu beachten. Um die Winkelgeschwindigkeit zu einem bestimmten Zeitpunkt zu bestimmen, ist es erforderlich, ein extrem kleines Zeitintervall zu betrachten, sodass die Winkelgeschwindigkeit in diesem Zeitraum keine signifikanten Änderungen aufweist. Daher wird die momentane Winkelgeschwindigkeit durch Berechnung der durchschnittlichen Winkelgeschwindigkeit im Grenzwert eines gegen Null strebenden Zeitintervalls erhalten. Mathematisch betrachtet entspricht dies der Ableitung des Winkels nach der Zeit und repräsentiert die Steigung der Winkel-Zeit-Kurve.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn wir den zur ckgelegten Winkel als die Winkelvariation ($\Delta\theta$) zur Zeit $t+\Delta t$ und zur Zeit $t$ betrachten:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
und der Abgelaufene Zeit ($\Delta t$) verwenden, dann haben wir im Grenzfall unendlich kurzer Zeiten:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
Dieser letzte Ausdruck entspricht der Ableitung der Winkelfunktion $\theta(t)$, die wiederum die Steigung der grafischen Darstellung dieser Funktion ber der Zeit ist.
(ID 3232)
(ID 10968)
Da die Geschwindigkeit ($v$) mit die Augenblickliche Winkelgeschwindigkeit ($\omega$) und der Radio ($r$) gleich ist:
| $ v = r \omega $ |
k nnen wir die Geschwindigkeit (Vektor) ($\vec{v}$) mithilfe des Kreuzprodukts mit dem Achsvektor, bezeichnet als $\hat{n}$, und dem Radialvektor, bezeichnet als $\hat{r}$, berechnen:
$\hat{t} = \hat{n} \times \hat{r}$
Wenn wir also definieren
$\vec{v}=v\hat{t}$
,
$\vec{r}=r\hat{r}$
und
$\vec{\omega}=\omega\hat{n}$
,
k nnen wir die Geschwindigkeit ausdr cken als
$\vec{v}=v\hat{t}=v\hat{n}\times\hat{r}=r\omega\hat{n}\times\hat{r}=\vec{\omega}\times\vec{r}$
das hei t
| $ \vec{v} = \vec{\omega} \times \vec{r} $ |
(ID 11597)
Beispiele
(ID 15412)
Wenn wir zu einem Zeitpunkt $t$ einen Winkel $\theta(t)$ betrachten und zu einem zuk nftigen Zeitpunkt $t+\Delta t$ einen Winkel $\theta(t+\Delta t)$, k nnen wir die Geschwindigkeit als den zur ckgelegten Winkel
$\theta(t+\Delta t)-\theta(t)$
in der Zeit $\Delta t$ sch tzen.
$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ verringert wird, bernimmt die Winkelgeschwindigkeit die Rolle der Tangente zur Positions-Kurve zu diesem Zeitpunkt:

Dies verallgemeinert, was bereits f r den Fall konstanter Winkelgeschwindigkeit gesehen wurde.
(ID 11407)
Wenn wir feststellen, dass die Winkelgeschwindigkeit $\omega$ gleich dem Winkel $\Delta\theta$ multipliziert mit der Zeit $\Delta t$ ist, k nnen wir sagen, dass die Verschiebung
$\Delta\theta = \omega\Delta t$
ist. Da das Produkt $\omega\Delta t$ den Bereich unter der Kurve der Winkelgeschwindigkeit in Abh ngigkeit von der Zeit repr sentiert und dieser Bereich gleichzeitig der zur ckgelegten Verschiebung entspricht:

(ID 11417)
Das Integral einer Funktion entspricht der Fl che unter der Kurve, die die Funktion definiert. Daher entspricht das Integral der Geschwindigkeit zwischen den Zeiten $t_0$ und $t$ dem durchlaufenden Winkel zwischen der Ausgangsposition $\theta_0$ und $\theta$.
Dies kann mathematisch wie folgt ausgedr ckt werden:
| $ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$ |
Diese Beziehung wird grafisch unten dargestellt:

Diese Formel ist n tzlich, um den durchlaufenden Winkel eines Objekts in Situationen zu berechnen, in denen die Geschwindigkeitsfunktion bekannt ist. Das Integral der Geschwindigkeitsfunktion liefert ein Ma f r die Gesamtverschiebung des Objekts zwischen den beiden Zeiten $t_0$ und $t$, das zur Berechnung des durchlaufenden Winkels des Objekts verwendet werden kann, indem man die Verschiebung durch den Radius des Kreises teilt. Dieses Konzept ist besonders n tzlich in Physik- und Ingenieur-Anwendungen, in denen Rotationsbewegungen beteiligt sind.
(ID 11409)
Die Orientierung der Tangentialgeschwindigkeit kann mit der Rechten-Hand-Regel bestimmt werden. Wenn die Finger in Richtung der Rotationsachse zeigen und dann in Richtung des Positionsvektors (Radius) gebogen werden, zeigt der Daumen in Richtung der Tangentialgeschwindigkeit:

(ID 11599)
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung w rde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausf hrt, die dem Radius mal der Winkelgeschwindigkeit entspricht:

Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
(ID 310)
(ID 15423)
ID:(1447, 0)
