Storyboard

A microporosidade do solo depende da sua composição, portanto, é importante poder modelá-la com base na proporção das diferentes componentes. Para fazer isso, primeiro estuda-se o fator volumétrico das várias texturas e, em seguida, estima-se a porosidade, levando em consideração que há uma componente básica fornecida pela argila. Além disso, considera-se a presença de areia e silte, mas é importante notar que a argila pode penetrar nos espaços entre os grãos, o que reduz a porosidade total.

>Modelo

ID:(2050, 0)

Iframe

>Top

ID:(15199, 0)

Conceito

>Top

No caso dos solos em geral, podemos estudar o triângulo de textura do solo. Se descrevermos a faixa típica de porosidade observada para cada tipo de solo, podemos ver o que foi discutido anteriormente. No canto onde predomina a areia, temos uma porosidade que pode chegar até 25%, o que é ótimo para um modelo de esferas:

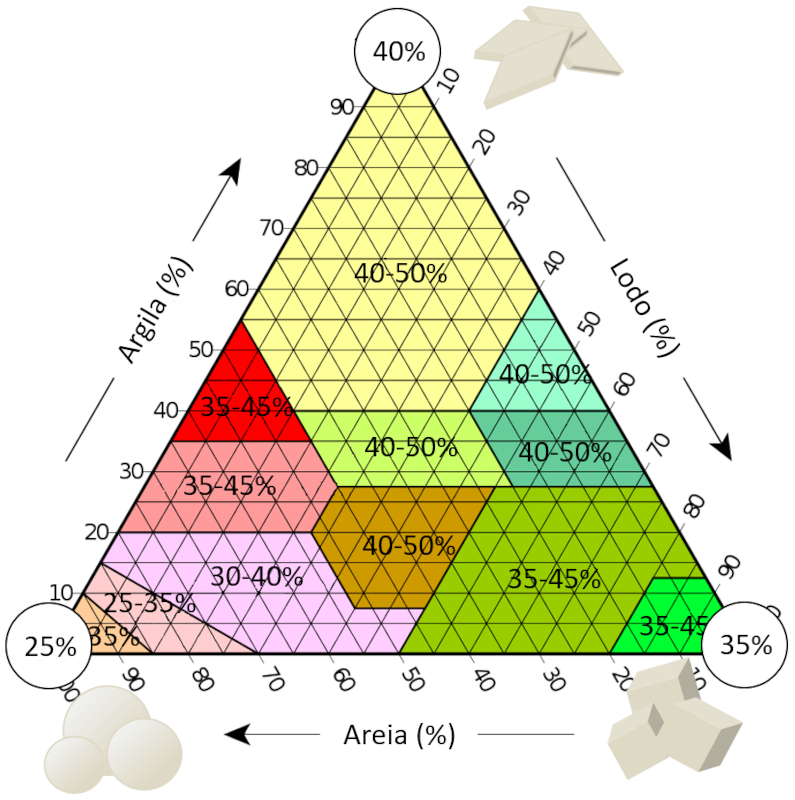
Triângulo de textura que inclui a faixa de porosidade obtida em [1] e [2].

Agora, se olharmos para o canto do silte, podemos ver que é possível alcançar uma porosidade de 35%, o que corresponde ao nível de espaço que não pode ser preenchido por cubos. Isso significa que o material não é capaz de se organizar de forma a aproveitar a estrutura cúbica. Isso provavelmente é uma consequência das forças atrativas na escala de micrômetros que resultam em empilhamento desordenado.

No último caso, podemos ver o limite da argila, onde a porosidade atinge um valor em torno de 40%, o que novamente deve ser uma consequência da interação entre as placas que podem organizar grupos delas, mas não o sistema inteiro.

Resumindo, observamos que no canto inferior esquerdo, onde o solo é principalmente composto por areia, a porosidade pode chegar a 25%. Esses 25% representam precisamente a porosidade alcançada no melhor cenário para um modelo de esferas.

Em outras palavras, existe uma porosidade inerente específica para os tipos de solo, e nos solos com uma presença significativa de argila, a argila domina. O efeito da areia e do silte só prevalece em casos extremos em que o material tem muito pouco argila.

[1] Soil Mechanics and Foundations, Muni Budhu, (2011), John Wiley & Sons.

[2] Principles of Geotechnical Engineering, Braja M. Das, (2010), Cengage Learning

ID:(2078, 0)

Conceito

>Top

Se assumirmos que as densidades dos diferentes componentes são semelhantes:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

os fatores volumétricos la fração volumétrica de areia na amostra ($f_a$), la fração volumétrica de lodo na amostra ($f_i$), la fração volumétrica de argila na amostra ($f_c$) em função de la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$) e la fração mássica de argila na amostra ($g_c$) podem ser expressos da seguinte forma:

$f_a = (1-f)\displaystyle\frac{\rho_s}{\rho_a}g_a \sim (1-f)g_a$

$f_i = (1-f)\displaystyle\frac{\rho_s}{\rho_i}g_i \sim (1-f)g_i$

$f_c = (1-f)\displaystyle\frac{\rho_s}{\rho_c}g_c \sim (1-f)g_c$

Isso nos permite estimar a faixa de fatores volumétricos para diferentes tipos de solos, incluindo quando la porosidade ($f$) e la fração volumétrica de macroporos na amostra ($f_m$) são nulos:

ID:(15096, 0)

Descrição

>Top

Dada a informação que temos para la temperatura em graus Celsius no estado 2 ($t_2$), o fator de volume próprio de areia ($p_a$), o fator de volume próprio do Slime ($p_i$), o fator de volume próprio da argila ($p_c$), la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$) e la fração mássica de argila na amostra ($g_c$), que satisfaz a equação:

e conhecemos os valores médios para diferentes texturas de solo com os respetivos la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$), la fração mássica de argila na amostra ($g_c$) e o cálculo da equação de porosidade ($p_p$) como:

Podemos realizar uma regressão para determinar os valores de o cálculo da equação de porosidade ($p_p$), o fator de volume próprio de areia ($p_a$) e o fator de volume próprio do Slime ($p_i$). O resultado é um ajuste com um R-quadrado de 0,974 e os parâmetros são os seguintes:

Em geral, o nível de compactação da areia com um la própria porosidade da areia ($q_a$) de aproximadamente 25% corresponde à máxima compactação. No entanto, com um la própria porosidade do lodo ($q_i$) de cerca de 47%, é maior do que o ótimo, assim como os 49% para la própria porosidade da argila ($q_c$). Em qualquer caso, os fatores são uma boa estimativa, dada a alta R-quadrado e os baixos valores de p-teste para cada fator, que são significativamente menores do que o limite tradicional de 0,05. Tentativas de considerar outras potências na regressão mostram que a aproximação linear é a única que gera coeficientes abaixo de 0,05, sugerindo que as amostras devem ter distribuições que não apresentam efeitos significativos de mistura e são simplesmente somas de componentes, como agregados.

ID:(15099, 0)

Top

>Top

Parâmetros

$\rho_c$

rho_c

Comprimento e largura de uma placa de argila

kg/m^3

$\rho_a$

rho_a

Densidade de um grão de areia

kg/m^3

$\rho_i$

rho_i

Densidade de um grão de lodo

kg/m^3

$\rho_s$

rho_s

Densidade sólida

kg/m^3

Variáveis

$p_p$

p_p

Cálculo da equação de porosidade

-

$p_c$

p_c

Fator de volume próprio da argila

-

$p_a$

p_a

Fator de volume próprio de areia

-

$p_i$

p_i

Fator de volume próprio do Slime

-

$f_c$

f_c

Força por grão

N

$g_i$

g_i

Fração de massa de lodo na amostra

-

$g_a$

g_a

Fração mássica de areia na amostra

-

$g_c$

g_c

Fração mássica de argila na amostra

-

$f_a$

f_a

Fração volumétrica de areia na amostra

-

$f_c$

f_c

Fração volumétrica de argila na amostra

-

$f_i$

f_i

Fração volumétrica de lodo na amostra

-

$f_m$

f_m

Fração volumétrica de macroporos na amostra

-

$f$

f

Porosidade

-

$q_a$

q_a

Própria porosidade da areia

-

$q_c$

q_c

Própria porosidade da argila

-

$q_i$

q_i

Própria porosidade do lodo

-

$V_m$

V_m

Volume de macroporos

m^3

$V_a$

V_a

Volume sólido de areia

m^3

$V_c$

V_c

Volume sólido de argila

m^3

$V_i$

V_i

Volume sólido de lodo

m^3

$V_t$

V_t

Volume total

m^3

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15218, 0)

Equação

>Top, >Modelo

Da mesma forma que definimos proporções entre as massas de cada componente e a massa total, podemos estabelecer um sistema análogo utilizando os volumes. Com isso em mente, podemos definir la fração volumétrica de areia na amostra ($f_a$) em relação ao o volume total ($V_t$). Isso nos permitirá calcular a quantidade de o volume sólido de areia ($V_a$) no contexto do o volume total ($V_t$).

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

Condições

Variáveis

$f_a$

Fração volumétrica de areia na amostra

$-$

10105

$V_a$

Volume sólido de areia

$m^3$

6554

$V_t$

Volume total

$m^3$

4946

Relação

ID:(10369, 0)

Equação

>Top, >Modelo

Da mesma forma que definimos proporções entre as massas de cada componente e a massa total, podemos estabelecer um sistema análogo utilizando os volumes. Com isso em mente, podemos definir la fração volumétrica de lodo na amostra ($f_i$) em relação ao o volume total ($V_t$). Isso nos permitirá calcular a quantidade de o volume sólido de lodo ($V_i$) no contexto do o volume total ($V_t$).

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

Condições

Variáveis

$f_i$

Fração volumétrica de lodo na amostra

$-$

10106

$V_i$

Volume sólido de lodo

$m^3$

6555

$V_t$

Volume total

$m^3$

4946

Relação

ID:(10367, 0)

Equação

>Top, >Modelo

De maneira semelhante à forma como são definidas as proporções entre as massas de cada componente e a massa total, podemos estabelecer um sistema análogo usando volumes. Com isso em mente, podemos definir la fração volumétrica de argila na amostra ($f_c$) em relação ao o volume total ($V_t$). Isso nos permitirá calcular a quantidade de o volume total ($V_t$) no contexto do volume total.

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

Condições

Variáveis

$f_c$

Força por grão

$N$

8270

$V_c$

Volume sólido de argila

$m^3$

6556

$V_t$

Volume total

$m^3$

4946

Relação

ID:(10368, 0)

Equação

>Top, >Modelo

De maneira semelhante à forma como são definidas as proporções entre as massas de cada componente e a massa total, podemos estabelecer um sistema análogo usando volumes. Com isso em mente, podemos definir la fração volumétrica de macroporos na amostra ($f_m$) em relação ao o volume total ($V_t$). Isso nos permitirá calcular a quantidade de o volume de macroporos ($V_m$) no contexto de o volume total ($V_t$).

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

Condições

Variáveis

$f_m$

Fração volumétrica de macroporos na amostra

$-$

10110

$V_m$

Volume de macroporos

$m^3$

10109

$V_t$

Volume total

$m^3$

4946

Relação

ID:(15084, 0)

Equação

>Top, >Modelo

A condição para solos argilosos com base em o volume sólido de areia ($V_a$), o volume sólido de lodo ($V_i$), o volume sólido de argila ($V_c$), o volume de macroporos ($V_m$), o volume próprio ($V_z$) e la própria porosidade da argila ($q_c$) é expressa da seguinte forma:

Quando usamos a equação para o volume total ($V_t$) em termos de o volume próprio ($V_z$) e a dividimos por o volume total ($V_t$), podemos reescrevê-la em termos de la fração volumétrica de areia na amostra ($f_a$), la fração volumétrica de lodo na amostra ($f_i$), la fração volumétrica de argila na amostra ($f_c$) e la fração volumétrica de macroporos na amostra ($f_m$) da seguinte maneira:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

Condições

Variáveis

$f_a$

Fração volumétrica de areia na amostra

$-$

10105

$f_c$

Fração volumétrica de argila na amostra

$-$

10107

$f_i$

Fração volumétrica de lodo na amostra

$-$

10106

$f_m$

Fração volumétrica de macroporos na amostra

$-$

10110

$q_a$

Própria porosidade da areia

$-$

10102

$q_c$

Própria porosidade da argila

$-$

10104

$q_i$

Própria porosidade do lodo

$-$

10103

Relação

Desenvolvimento

Com a equação do o volume total ($V_t$) em relação ao o volume próprio ($V_z$) e aos o volume de macroporos ($V_m$):

$ V_t = V_m + V_z $

Substituindo o o volume próprio ($V_z$) em termos do o volume sólido de areia ($V_a$), o volume sólido de lodo ($V_i$), o volume sólido de argila ($V_c$), o volume de macroporos ($V_m$) e do la própria porosidade da argila ($q_c$) com:

$ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$

obtemos:

$V_t = V_a + V_i + \displaystyle\frac{1}{1-q_c}V_c+V_m$

Se dividirmos esta equação por o volume total ($V_t$) e usarmos as definições de la fração volumétrica de areia na amostra ($f_a$)

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

para o la fração volumétrica de lodo na amostra ($f_i$)

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

para o la fração volumétrica de argila na amostra ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

e para os la fração volumétrica de macroporos na amostra ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

obtemos a seguinte relação:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

ID:(15086, 0)

Equação

>Top, >Modelo

O volume de poro ($V_p$) em um material argiloso, que é uma função do volume dos o volume de macroporos ($V_m$), la própria porosidade da argila ($q_c$) e o volume sólido de argila ($V_c$):

pode ser reescrita dividindo a equação por o volume total ($V_t$) e expressando a equação em termos da la porosidade ($f$), la fração volumétrica de macroporos na amostra ($f_m$) e la fração volumétrica de argila na amostra ($f_c$), resultando em:

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Condições

Variáveis

$f_a$

Fração volumétrica de areia na amostra

$-$

10105

$f_c$

Fração volumétrica de argila na amostra

$-$

10107

$f_i$

Fração volumétrica de lodo na amostra

$-$

10106

$f$

Porosidade

$-$

5805

$q_a$

Própria porosidade da areia

$-$

10102

$q_c$

Própria porosidade da argila

$-$

10104

$q_i$

Própria porosidade do lodo

$-$

10103

Relação

Desenvolvimento

O cálculo do o volume de poro ($V_p$) pode ser realizado utilizando os volumes de o volume de macroporos ($V_m$), o volume sólido de argila ($V_c$) e la própria porosidade da argila ($q_c$) com a seguinte equação:

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

Ao dividir esta equação pelo o volume total ($V_t$), podemos utilizar la porosidade ($f$)

$ f =\displaystyle\frac{ V_p }{ V_t }$

juntamente com o la fração volumétrica de macroporos na amostra ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

e o la fração volumétrica de argila na amostra ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

o que simplifica para

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

.

ID:(2074, 0)

Equação

>Top, >Modelo

Como la fração volumétrica de areia na amostra ($f_a$) foi definido em termos de o volume sólido de areia ($V_a$) e o volume total ($V_t$):

Portanto, com la densidade de um grão de areia ($\rho_a$), la densidade sólida ($\rho_s$), la porosidade ($f$) e la fração mássica de areia na amostra ($g_a$) você pode calcular o fator usando:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

Condições

Variáveis

$\rho_a$

Densidade de um grão de areia

2.63e+3

$kg/m^3$

10095

$\rho_s$

Densidade sólida

$kg/m^3$

4944

$g_a$

Fração mássica de areia na amostra

$-$

5797

$f_a$

Fração volumétrica de areia na amostra

$-$

10105

$f$

Porosidade

$-$

5805

Relação

Desenvolvimento

Para calcular la fração volumétrica de areia na amostra ($f_a$), você pode utilizar a definição com o volume sólido de areia ($V_a$) e o volume total ($V_t$) da seguinte forma:

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

o volume sólido de areia ($V_a$) pode ser expresso com la densidade de um grão de areia ($\rho_a$) e la massa seca de areia na amostra ($M_a$) usando a equação:

$ V_a =\displaystyle\frac{ M_a }{ \rho_a }$

Para o volume total ($V_t$), você pode trabalhar com o volume sólido ($V_s$) e o volume de poro ($V_p$) usando a equação:

$ V_t = V_s + V_p $

utilizando a expressão para la porosidade ($f$):

$ f =\displaystyle\frac{ V_p }{ V_t }$

Com ambas as equações, você obtém a expressão:

$V_t = \displaystyle\frac{1}{1-f} V_s$

Usando a definição de la densidade sólida ($\rho_s$) com la massa seca total da amostra ($M_s$) e o volume sólido ($V_s$):

$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$

você pode expressar o volume total ($V_t$) como:

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

Desta forma, você obtém a expressão para la fração volumétrica de areia na amostra ($f_a$) como:

$f_a= \displaystyle\frac{V_a}{V_t}= \displaystyle\frac{M_a}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_a}$

que, com a equação para la fração mássica de areia na amostra ($g_a$):

$ g_a =\displaystyle\frac{ M_a }{ M_s }$

se reduz a:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

ID:(15093, 0)

Equação

>Top, >Modelo

Como la fração volumétrica de areia na amostra ($f_a$) foi definido em relação a o volume sólido de lodo ($V_i$) e o volume total ($V_t$):

Portanto, com la densidade de um grão de lodo ($\rho_i$), la densidade sólida ($\rho_s$), la porosidade ($f$) e la fração de massa de lodo na amostra ($g_i$), você pode calcular o fator usando:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

Condições

Variáveis

$\rho_i$

Densidade de um grão de lodo

2.65e+3

$kg/m^3$

10094

$\rho_s$

Densidade sólida

$kg/m^3$

4944

$g_i$

Fração de massa de lodo na amostra

$-$

10098

$f_i$

Fração volumétrica de lodo na amostra

$-$

10106

$f$

Porosidade

$-$

5805

Relação

ID:(15094, 0)

Equação

>Top, >Modelo

Como la fração volumétrica de areia na amostra ($f_a$) foi definido em relação a o volume sólido de argila ($V_c$) e o volume total ($V_t$):

Portanto, com la comprimento e largura de uma placa de argila ($\rho_c$), la densidade sólida ($\rho_s$), la porosidade ($f$) e la fração mássica de argila na amostra ($g_c$), você pode calcular o fator utilizando:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

Condições

Variáveis

$\rho_c$

Comprimento e largura de uma placa de argila

2.8e+3

$kg/m^3$

10093

$\rho_s$

Densidade sólida

$kg/m^3$

4944

$g_c$

Fração mássica de argila na amostra

$-$

10099

$f_c$

Fração volumétrica de argila na amostra

$-$

10107

$f$

Porosidade

$-$

5805

Relação

ID:(15095, 0)

Equação

>Top, >Modelo

La porosidade ($f$) é uma função de la fração volumétrica de macroporos na amostra ($f_m$), la fração volumétrica de areia na amostra ($f_a$), la fração volumétrica de lodo na amostra ($f_i$), la fração volumétrica de argila na amostra ($f_c$), la própria porosidade da areia ($q_a$), la própria porosidade do lodo ($q_i$) e la própria porosidade da argila ($q_c$):

Usando as relações entre os fatores volumétricos e os fatores de massa la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$) e la fração mássica de argila na amostra ($g_c$), assumindo a ausência de macroporos e densidades iguais para as três componentes, obtemos:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Condições

Variáveis

$g_i$

Fração de massa de lodo na amostra

$-$

10098

$g_a$

Fração mássica de areia na amostra

$-$

5797

$g_c$

Fração mássica de argila na amostra

$-$

10099

$f$

Porosidade

$-$

5805

$q_a$

Própria porosidade da areia

$-$

10102

$q_c$

Própria porosidade da argila

$-$

10104

$q_i$

Própria porosidade do lodo

$-$

10103

Relação

Desenvolvimento

La porosidade ($f$) é uma função de o número de grãos de lodo na amostra ($N_i$), la fração volumétrica de areia na amostra ($f_a$), la fração volumétrica de lodo na amostra ($f_i$), la fração volumétrica de argila na amostra ($f_c$), la própria porosidade da areia ($q_a$), la própria porosidade do lodo ($q_i$) e la própria porosidade da argila ($q_c$):

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Dado que com la densidade sólida ($\rho_s$), la densidade de um grão de areia ($\rho_a$) e la fração mássica de areia na amostra ($g_a$) temos:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

e com la densidade de um grão de lodo ($\rho_i$) e la fração de massa de lodo na amostra ($g_i$) temos:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

Além disso, com la comprimento e largura de uma placa de argila ($\rho_c$) e la fração mássica de argila na amostra ($g_c$) temos:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

é possível, no caso em que as densidades são iguais:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

e não existem macroporos:

$f_m\sim 0$

obter a seguinte relação:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

.

ID:(10370, 0)

Equação

>Top, >Modelo

Com la própria porosidade da areia ($q_a$), você pode definir o fator de volume próprio de areia ($p_a$) da seguinte forma:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

Condições

Variáveis

$p_a$

Fator de volume próprio de areia

$-$

6557

$q_a$

Própria porosidade da areia

$-$

10102

Relação

ID:(15087, 0)

Equação

>Top, >Modelo

Com la própria porosidade do lodo ($q_i$), você pode definir o fator de volume próprio do Slime ($p_i$) da seguinte forma:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

Condições

Variáveis

$p_i$

Fator de volume próprio do Slime

$-$

6558

$q_i$

Própria porosidade do lodo

$-$

10103

Relação

ID:(15088, 0)

Equação

>Top, >Modelo

Com la própria porosidade da argila ($q_c$), você pode definir o fator de volume próprio da argila ($p_c$) da seguinte forma:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Condições

Variáveis

$p_c$

Fator de volume próprio da argila

$-$

6559

$q_c$

Própria porosidade da argila

$-$

10104

Relação

ID:(15098, 0)

Equação

>Top, >Modelo

Com la porosidade ($f$), você pode definir o cálculo da equação de porosidade ($p_p$) da seguinte forma:

$ p_p = \displaystyle\frac{ f }{1- f }$

Condições

Variáveis

$p_p$

Cálculo da equação de porosidade

$-$

6053

$f$

Porosidade

$-$

5805

Relação

ID:(2076, 0)

Equação

>Top, >Modelo

Usando la porosidade ($f$), la própria porosidade da areia ($q_a$), la própria porosidade do lodo ($q_i$), la própria porosidade da argila ($q_c$), la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$) e la fração mássica de argila na amostra ($g_c$),

pode ser reescrito com as definições de o cálculo da equação de porosidade ($p_p$), o fator de volume próprio de areia ($p_a$), o fator de volume próprio do Slime ($p_i$) e o fator de volume próprio da argila ($p_c$) da seguinte forma:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

Condições

Variáveis

$p_p$

Cálculo da equação de porosidade

$-$

6053

$p_c$

Fator de volume próprio da argila

$-$

6559

$p_a$

Fator de volume próprio de areia

$-$

6557

$p_i$

Fator de volume próprio do Slime

$-$

6558

$g_i$

Fração de massa de lodo na amostra

$-$

10098

$g_a$

Fração mássica de areia na amostra

$-$

5797

$g_c$

Fração mássica de argila na amostra

$-$

10099

Relação

Desenvolvimento

Com as variáveis la porosidade ($f$), la própria porosidade da areia ($q_a$), la própria porosidade do lodo ($q_i$), la própria porosidade da argila ($q_c$), la fração mássica de areia na amostra ($g_a$), la fração de massa de lodo na amostra ($g_i$) e la fração mássica de argila na amostra ($g_c$), temos a seguinte relação:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Se considerarmos a relação para o cálculo da equação de porosidade ($p_p$) como:

$ p_p = \displaystyle\frac{ f }{1- f }$

A relação para o fator de volume próprio de areia ($p_a$) como:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

A relação para o fator de volume próprio do Slime ($p_i$) como:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

E a relação para o fator de volume próprio da argila ($p_c$) como:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Então o resultado geral é:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

ID:(1542, 0)