Benützer:
Innenströmung und Erosion
Storyboard 
Der innere Fluss erfolgt durch die Kapillaren, die sich zwischen den Bodenpartikeln bilden. Immer wenn diese Kapillaren Abmessungen haben, die größer sind als die der kleinen Tonplatten, besteht die Gefahr, dass diese Tonpartikel durch diesen Fluss mitgerissen werden. Wenn dies geschieht, könnte der Boden einen Teil seines Tonanteils verlieren, was sich auf seine mechanischen Eigenschaften, Stabilität und Unterstützung für das organische Leben auswirken würde.
ID:(379, 0)
Energie Dichte
Gleichung
Da ein Fluid oder Gas ein Kontinuum ist, kann das Konzept der Energie nicht mehr mit einer spezifischen Masse verbunden werden. Es ist jedoch möglich, die Energie in einem Volumen des Kontinuums zu betrachten und durch Division durch das Volumen selbst erhalten wir die Energiedichte ($e$). Daher haben wir mit die Dichte ($\rho$), die Geschwindigkeit auf einer Zylinder-Radio ($v$), die Höhe der Säule ($h$), die Gravitationsbeschleunigung ($g$) und die Druck der Wassersäule ($p$):
 $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
Eine weitere nützliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in Fällen angewendet wird, in denen die Viskosität vernachlässigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine äußere Kraft, die die Flüssigkeit über eine Strecke $\Delta z$ verschiebt, berücksichtigt, kann sie wie folgt ausgedrückt werden:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, können wir die Masse ersetzen durch:
$m=\rho \Delta x\Delta y\Delta z$
Und da der Druck gegeben ist durch:
$F=p \Delta S =p \Delta y\Delta z$
erhalten wir die Gleichung für die Energiedichte:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
was der Bernoulli-Gleichung entspricht.
ID:(3159, 0)
Allgemeine Bernoulli-Gleichung
Gleichung
Mit die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$), die Höhe oder Tiefe 1 ($h_1$) und die Druck in Spalte 1 ($p_1$), die die Geschwindigkeit, die Höhe und den Druck am Punkt 1 repräsentieren, und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$), die Höhe oder Tiefe 2 ($h_2$) und die Druck in Spalte 2 ($p_2$), die die Geschwindigkeit, die Höhe und den Druck am Punkt 2 repräsentieren, haben wir:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
Angenommen, dass die Energiedichte ($e$) erhalten bleibt, können wir feststellen, dass für eine Zelle, in der die Durchschnittsgeschwindigkeit die Geschwindigkeit auf einer Zylinder-Radio ($v$) beträgt, die Dichte die Dichte ($\rho$), der Druck die Druck der Wassersäule ($p$), die Höhe die Höhe der Säule ($h$) und die Gravitationsbeschleunigung die Gravitationsbeschleunigung ($g$) folgendes gilt:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
An Punkt 1 wird diese Gleichung gleich der gleichen Gleichung an Punkt 2 sein:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
wobei die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$), die Höhe oder Tiefe 1 ($h_1$) und die Druck in Spalte 1 ($p_1$) die Geschwindigkeit, Höhe und Druck an Punkt 1 darstellen und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$), die Höhe oder Tiefe 2 ($h_2$) und die Druck in Spalte 2 ($p_2$) die Geschwindigkeit, Höhe und Druck an Punkt 2 darstellen. Daher haben wir:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
ID:(4504, 0)
Bernoulli-Gleichung, Variationen
Gleichung
Die Variación de la Presión ($\Delta p$) kann aus die Durchschnittsgeschwindigkeit ($\bar{v}$) und die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) mit die Dichte ($\rho$) berechnet werden
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Für den Fall, dass kein hystrostatischer Druck vorhanden ist, gilt das Bernoulli-Gesetz für die Dichte ($\rho$), die Druck in Spalte 1 ($p_1$), die Druck in Spalte 2 ($p_2$), die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und < var>5416
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
kann mit umgeschrieben werden die Variación de la Presión ($\Delta p$)
| $ \Delta p = p_2 - p_1 $ |
und das im Hinterkopf behalten
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
mit
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
Und
| $ \Delta v = v_2 - v_1 $ |
du musst
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Dies ermöglicht es uns, den Einfluss der Durchschnittsgeschwindigkeit eines Körpers und des Unterschieds zwischen seinen Oberflächen zu sehen, wie er bei einem Flugzeug oder einem Vogelflügel beobachtet wird.
ID:(4835, 0)
Strömung nach Hagen-Poiseuillee Gleichung
Konzept
Das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) in der Positionsradius in einem Rohr ($r$) ermöglicht es uns, der Volumenstrom ($J_V$) in einem Rohr durch Integration über die gesamte Oberfläche zu berechnen, was zur bekannten Hagen-Poiseuille-Gesetz führt.
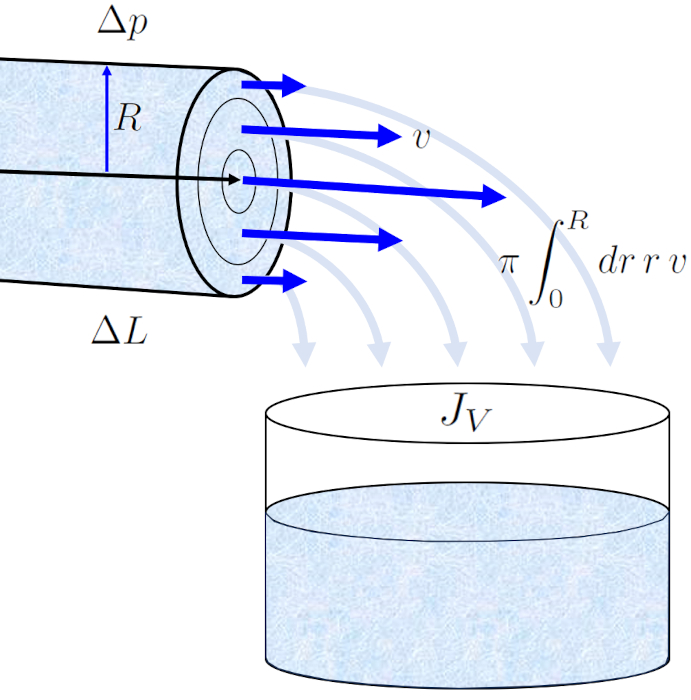
Das Ergebnis ist eine Gleichung, die von Rohrradius ($R$) zur vierten Potenz abhängt. Es ist jedoch entscheidend zu beachten, dass dieses Strömungsprofil nur im Falle einer laminaren Strömung gültig ist.
Daraus ergibt sich mit die Viskosität ($\eta$), dass der Volumenstrom ($J_V$) vor ein Rohrlänge ($\Delta L$) und eine Variación de la Presión ($\Delta p$) die Ausdruck:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Die Originalarbeiten, die zu diesem Gesetz mit einem kombinierten Namen führten, waren:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Experimentelle Untersuchungen zur Bewegung von Flüssigkeiten in Röhren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Geschwindigkeitsprofil eines zylindrischen Strömung
Gleichung
Beim Lösen der Fließgleichung mit der Randbedingung erhalten wir die Geschwindigkeit auf einer Zylinder-Radio ($v$) als Funktion von der Krümmung Radio ($r$), dargestellt als Parabel mit dem Mittelpunkt bei die Maximale Durchflussrate ($v_{max}$) und Nullwert bei der Rohrradius ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Wenn eine die Druckunterschied ($\Delta p_s$) auf einen Abschnitt mit einer Fläche von $\pi R^2$ wirkt, wobei der Rohrradius ($R$) als der Krümmung Radio ($r$) fungiert, erzeugt sie eine Kraft, die wie folgt dargestellt wird:
$\pi r^2 \Delta p$
Diese Kraft treibt die Flüssigkeit gegen den Viskosewiderstand an, der durch folgenden Ausdruck gegeben ist:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Durch das Gleichsetzen dieser beiden Kräfte erhalten wir:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Dies führt zu folgender Gleichung:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Wenn wir diese Gleichung von einer Position, die durch der Krümmung Radio ($r$) definiert ist, bis zum Rand, wo der Rohrradius ($R$) ist (unter Berücksichtigung, dass die Geschwindigkeit am Rand null ist), integrieren, können wir die Geschwindigkeit auf einer Zylinder-Radio ($v$) als Funktion von der Krümmung Radio ($r$) erhalten:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Dabei ist:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
die Maximale Durchflussrate ($v_{max}$) in der Mitte des Flusses.
.
ID:(3627, 0)
Maximale Geschwindigkeit der Strömung in einem Zylinder
Gleichung
Der Wert von die Maximale Durchflussrate ($v_{max}$) in der Mitte eines Zylinders hängt von die Viskosität ($\eta$), der Rohrradius ($R$) und dem Gradienten ab, der von die Druckunterschied ($\Delta p_s$) und der Rohrlänge ($\Delta L$) erzeugt wird, wie unten dargestellt:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Das negative Vorzeichen deutet darauf hin, dass der Fluss immer in entgegengesetzter Richtung zum Gradienten erfolgt, d.h., von der Region mit höherem Druck zur Region mit niedrigerem Druck.
ID:(3628, 0)
Condición de erosión generalizada
Gleichung
La plaquita de arcilla sera arrastrada por la corriente en la medida que la fuerza hidrostática
Por ello la condición de ser arrastrada es:
| $ dp S > m g $ |
ID:(4506, 0)
Masa de Plaquita de Arcilla
Gleichung
La masa de la plaquita se puede calcular de la densidad solida del material y del volumen mediante\\n\\n
$m=\rho_sV$
\\n\\nEl volumen se calcula del cuadrado del lado
$V=w_cl_c^2$
Con ello la masa del la plaquita es:
| $ m = \rho_s w_c l_c ^2$ |
ID:(4508, 0)
Sección de Plaquita de Arcilla
Gleichung
La sección
| $ S = l_c ^ 2$ |
ID:(4507, 0)
Condición de erosión en función de geometría
Gleichung
La condición de estabilidad general
| $ dp S > m g $ |
se puede reescribir con la masa
| $ m = \rho_s w_c l_c ^2$ |
y la sección
| $ S = l_c ^ 2$ |
como
| $dp > \rho_s w_c g $ |
ID:(10630, 0)