Utilizador:
Fluxo interior e erosão
Storyboard 
O fluxo interno ocorre através dos capilares formados entre as partículas do solo. Sempre que esses capilares têm dimensões maiores do que as das pequenas placas de argila, existe o risco de que essas partículas de argila sejam arrastadas por esse fluxo. Se isso acontecer, o solo poderá perder parte de seu teor de argila, o que afetaria suas propriedades mecânicas, estabilidade e suporte para a vida orgânica.
ID:(379, 0)
Densidade de energia
Equação
Uma vez que um fluido ou gás é um contínuo, o conceito de energia já não pode ser associado a uma massa específica. No entanto, é possível considerar a energia contida num volume do contínuo e, ao dividir pela própria volume, obtemos la densidade de energia ($e$). Portanto, com la densidade ($\rho$), la velocidade em um raio do cilindro ($v$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão da coluna de água ($p$), temos:
 $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
Outra equação útil é aquela que corresponde à conservação de energia, a qual é aplicável em casos em que a viscosidade, um processo que resulta em perda de energia, pode ser negligenciada. Se considerarmos a equação clássica da energia $E$, que leva em conta a energia cinética, a energia potencial gravitacional e uma força externa que desloca o líquido por uma distância $\Delta z$, podemos expressá-la da seguinte forma:
$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$
Se considerarmos a energia em um volume $\Delta x\Delta y\Delta z$, podemos substituir a massa por:
$m=\rho \Delta x\Delta y\Delta z$
E como a pressão é dada por:
$F=p \Delta S =p \Delta y\Delta z$
Obtemos a equação para a densidade de energia:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
o que corresponde à equação de Bernoulli.
ID:(3159, 0)
Equação geral de Bernoulli
Equação
Com la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representando a velocidade, altura e pressão no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representando a velocidade, altura e pressão no ponto 2, respectivamente, temos:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
Se assumirmos que la densidade de energia ($e$) é conservado, podemos afirmar que para uma célula onde a velocidade média é La velocidade em um raio do cilindro ($v$), a densidade é La densidade ($\rho$), a pressão é La pressão da coluna de água ($p$), a altura é La altura da coluna ($h$) e a aceleração gravitacional é La aceleração gravitacional ($g$), temos o seguinte:
| $ e =\displaystyle\frac{1}{2} \rho v ^2+ \rho g h + p $ |
Em um ponto 1, essa equação será igual à mesma equação em um ponto 2:
$e(v_1,p_1,h_1)=e(v_2,p_2,h_2)$
onde la velocidade média do fluido no ponto 1 ($v_1$), la hauteur ou profondeur 1 ($h_1$) e la pressão na coluna 1 ($p_1$) representam a velocidade, altura e pressão no ponto 1, respectivamente, e la velocidade média do fluido no ponto 2 ($v_2$), la hauteur ou profondeur 2 ($h_2$) e la pressão na coluna 2 ($p_2$) representam a velocidade, altura e pressão no ponto 2, respectivamente. Portanto, temos:
| $\displaystyle\frac{1}{2} \rho v_1 ^2+ \rho g h_1 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2+ \rho g h_2 + p_2 $ |
ID:(4504, 0)
Equação de Bernoulli, variações
Equação
($$) pode ser calculado a partir de la velocidade média ($\bar{v}$) e la diferença de velocidade entre superfícies ($\Delta v$) com la densidade ($\rho$) usando
| $ \Delta p = - \rho \bar{v} \Delta v $ |
No caso em que não há pressão hisstrostática, aplica-se a lei de Bernoulli para la densidade ($\rho$), la pressão na coluna 1 ($p_1$), la pressão na coluna 2 ($p_2$), la velocidade média do fluido no ponto 1 ($v_1$) e < var>5416
| $\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $ |
| $ \Delta p = p_2 - p_1 $ |
e tendo em mente que
$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$
com
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
e
| $ \Delta v = v_2 - v_1 $ |
se tem que
| $ \Delta p = - \rho \bar{v} \Delta v $ |
o que nos permite ver o efeito da velocidade média de um corpo e a diferença entre suas superfícies, como observado na asa de um avião ou de um pássaro.
ID:(4835, 0)
Fluxo de acordo com a equação de Hagen-Poiseuille
Conceito
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo através da integração de toda a superfície, o que nos leva à conhecida lei de Hagen-Poiseuille.
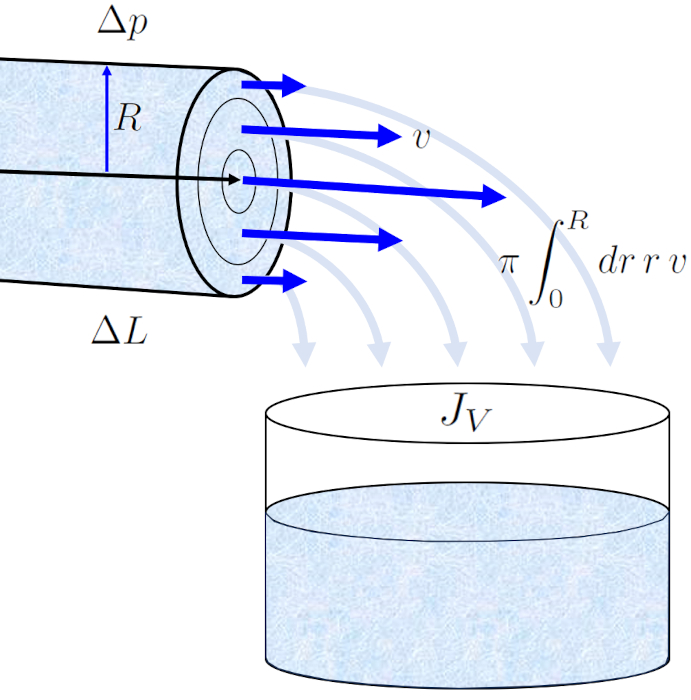
O resultado é uma equação que depende de raio do tubo ($R$) elevado à quarta potência. No entanto, é fundamental observar que este perfil de fluxo só é válido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ($$), a expressão:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (Sobre as leis que regem o fluxo da água em recipientes cilíndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Pesquisa experimental sobre o movimento de líquidos em tubos de diâmetros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Perfil de velocidade de um fluxo através de um cilindro
Equação
Ao resolver a equação de fluxo com a condição de contorno, obtemos la velocidade em um raio do cilindro ($v$) como uma função de o raio de curvatura ($r$), representada por uma parábola centrada em la taxa de fluxo máxima ($v_{max}$) e igual a zero em o raio do tubo ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Quando uma la diferença de pressão ($\Delta p_s$) age sobre uma seção com uma área de $\pi R^2$, com o raio do tubo ($R$) como o raio de curvatura ($r$), ela gera uma força representada por:
$\pi r^2 \Delta p$
Essa força impulsiona o líquido contra a resistência viscosa, dada por:
Ao igualarmos essas duas forças, obtemos:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
O que nos leva à equação:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Se integrarmos essa equação de uma posição definida por o raio de curvatura ($r$) até a borda onde o raio do tubo ($R$) está (levando em consideração que a velocidade na borda é zero), podemos obter la velocidade em um raio do cilindro ($v$) como função de o raio de curvatura ($r$):
Onde:
é La taxa de fluxo máxima ($v_{max}$) no centro do fluxo.
.
ID:(3627, 0)
Velocidade máxima no fluxo através de um cilindro
Equação
O valor de la taxa de fluxo máxima ($v_{max}$) no centro de um cilindro depende de la viscosidade ($\eta$), o raio do tubo ($R$) e do gradiente criado por la diferença de pressão ($\Delta p_s$) e o comprimento do tubo ($\Delta L$), conforme representado abaixo:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
O sinal negativo indica que o fluxo sempre ocorre na direção oposta ao gradiente, ou seja, da área de maior pressão para a área de menor pressão.
ID:(3628, 0)