Utilisateur:
Pression hydrostatique
Storyboard 
Dans le cas d'un sol saturé, la porosité est remplie d'eau. La présence d'eau implique une masse supplémentaire et l'existence d'une pression en fonction de la profondeur. Ces deux facteurs auront un impact sur le comportement du sol.
ID:(368, 0)
Description de la colonne d'eau
Concept
Pour étudier le comportement des liquides, il est utile d'introduire le concept de colonne de liquide. Cette colonne est une abstraction d'un contenant cylindrique (comme une éprouvette graduée) contenant du liquide, et permet d'étudier la force à laquelle un objet à l'intérieur est exposé.
Une fois ce concept introduit, nous pouvons penser à son existence indépendamment du contenant qui le contient. Par exemple, un plongeur nageant en haute mer est exposé au poids généré par une "colonne" imaginaire de liquide qui existe au-dessus de lui, de la surface du liquide jusqu'à sa peau et la surface de la mer.
a masse de colonne de liquide ($M$) peut être calculé à partir de a densité du liquide ($\rho_w$) et le volume de la colonne ($V$).
Pour calculer a densité du liquide ($\rho_w$), on utilise l'équation suivante :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
Et pour le volume de la colonne ($V$), l'équation est la suivante :
| $ V = S h $ |
De cette manière, la valeur de a masse de colonne de liquide ($M$) est obtenue par :
| $ M = \rho_w S h $ |
Ceci est valide tant que a hauteur de la colonne de liquide ($S$) reste constant tout au long de a hauteur de la colonne ($h$).
La section peut changer de forme, mais pas de surface.
ID:(2207, 0)
Force de l'eau sur le bas de la colonne
Concept
Une fois que le volume et donc la masse de la colonne sont connus, la force qu'elle exerce sur sa base peut être calculée. Il est important de noter que cela s'applique aux liquides considérés comme incompressibles, ce qui signifie que les couches inférieures du liquide sont supposées ne pas être compressées par le poids des couches supérieures.
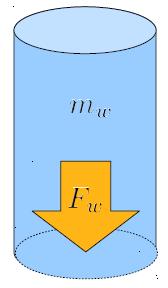
Ce principe peut être appliqué pour calculer la force exercée par n'importe quel liquide, tel que l'eau ou l'huile, et est particulièrement utile en ingénierie hydraulique et en mécanique des fluides.
Étant donné que a masse de colonne de liquide ($M$) dépend de a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) selon l'équation :
| $ M = \rho_w S h $ |
et que a force de la colonne ($F$) est représenté par a accélération gravitationnelle ($g$) par :
| $ F_g = m_g g $ |
alors l'expression peut être écrite comme suit :
| $ F = S h \rho_w g $ |
.
ID:(2208, 0)
Introduction de la notion de pression
Concept
En mécanique, nous décrivons comment les corps de masse définie se déplacent. Dans le cas d'un liquide, son mouvement n'est pas uniforme, et chaque section du liquide se déplace différemment. Cependant, ces \\"sections\\" n'ont pas une masse définie, car elles ne sont pas des objets définis ou séparés.
Pour résoudre ce problème, nous pouvons segmenter le liquide en une série de petits volumes séparés et, si possible, estimer leur masse en utilisant la densité. De cette manière, nous pouvons introduire l\'idée que les forces définissent le mouvement du liquide.
Cependant, en dernière analyse, les volumes sont arbitraires, et ce qui finit par générer le mouvement est la force agissant sur la face du volume. Par conséquent, il est plus logique d'introduire le concept de force de la colonne ($F$) par un tel hauteur de la colonne de liquide ($S$), appelé A pression de la colonne d'eau ($p$).
ID:(46, 0)
Pression d'eau en bas de colonne
Concept
La a force de la colonne ($F$) agissant sur le fond dépend de a hauteur de la colonne de liquide ($S$) dans le sens où si cette dernière varie, la force variera dans la même proportion. Dans ce sens, a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) ne sont pas interdépendants ; ils varient de manière proportionnelle. Il est logique de définir cette proportion comme a pression ($p$) :
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
Ceci est la loi de la pression hydrostatique, également connue sous le nom de loi de Pascal, principalement attribuée à Blaise Pascal [1].
[1] "Traité de l'équilibre des liqueurs", Blaise Pascal, 1663.
ID:(2085, 0)
Somme de la pression de colonne et de l'atmosphère
Concept
Si l'on considère que la colonne est sous l'influence de a pression atmosphèrique ($p_0$), alors la contribution de a pression atmosphèrique ($p_0$) doit être ajoutée à A pression de la colonne d'eau ($p$) de la colonne, comme illustré ici :
Lors du calcul de a pression de la colonne d'eau ($p$) à une certaine profondeur, il est important de prendre en compte que la surface du liquide est exposée à A pression atmosphèrique ($p_0$), ce qui peut affecter la valeur de la pression à cet endroit. Par conséquent, il est nécessaire de généraliser l'équation de a pression de la colonne d'eau ($p$) pour inclure non seulement la colonne de liquide a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$) et a accélération gravitationnelle ($g$), mais également a pression atmosphèrique ($p_0$) :
| $ p_t = p_0 + \rho_w g h $ |
Il n'est pas toujours nécessaire de prendre en compte la pression atmosphérique dans la modélisation :
Dans de nombreux cas, la pression atmosphérique est présente dans tout le système, de sorte que les différences de pression ne dépendent pas d'elle.
ID:(2210, 0)
Connexion de deux colonnes de liquide
Concept
En reliant deux colonnes d'eau de hauteurs différentes à leur base, on obtient une situation où il existe une différence de pression le long du tuyau connecteur.
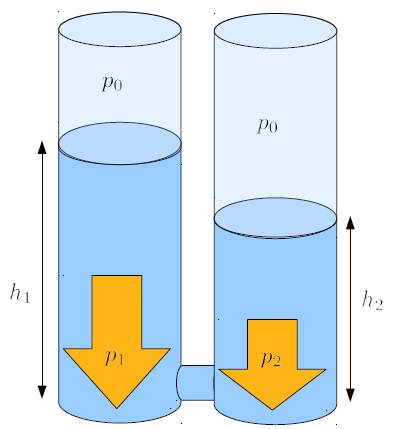
Ce montage nous permet d'étudier comment la différence de pression génère un mouvement de liquide le long du tuyau. On peut considérer un élément de liquide d'une certaine longueur avec une section égale à celle du tuyau et, en utilisant la densité, estimer la masse correspondante. Avec la section, on peut également convertir la différence de pression en une différence de forces et ainsi étudier comment les volumes de liquides sont accélérés en raison des différences de pression.
ID:(933, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta h = h_2 - h_1 $
Dh = h_2 - h_1
$ \Delta p = p_2 - p_1 $
Dp = p_2 - p_1
$ \Delta p = \rho_w g \Delta h $
Dp = rho_w * g * Dh
$ F = S h \rho_w g $
F = S * h * rho_w * g
$ M = \rho_w S h $
M = rho_w * S * h
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
$ p = \rho_w g h $
p = rho_w * g * h
$ p_t = p_0 + \rho_w g h $
p_t = p_0 + rho_w * g * h
$ \rho_w = \displaystyle\frac{ M }{ V }$
rho_w = M / V
$ V = S h $
V = S * h
ID:(15220, 0)
Volume de la colonne
Équation
Le volume de la colonne ($V$) est déterminé par a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) et est calculé comme suit :
| $ V = S h $ |
ID:(931, 0)
Densité d'un liquide
Équation
La a densité du liquide ($\rho_w$) est calculée à partir de a masse de colonne de liquide ($M$) et le volume de la colonne ($V$) en utilisant l'équation :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
ID:(15091, 0)
Masse de la colonne d'eau
Équation
En utilisant a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$), vous pouvez calculer a masse de colonne de liquide ($M$) avec la formule :
| $ M = \rho_w S h $ |
A masse de colonne de liquide ($M$) peut être calculé à partir de a densité du liquide ($\rho_w$) et le volume de la colonne ($V$).
Pour calculer a densité du liquide ($\rho_w$), on utilise l'équation suivante :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
Et pour le volume de la colonne ($V$), l'équation est la suivante :
| $ V = S h $ |
De cette manière, la valeur de a masse de colonne de liquide ($M$) est obtenue par :
| $ M = \rho_w S h $ |
ID:(4340, 0)
Force de la colonne d'eau
Équation
A force de la colonne ($F$) est calculé à partir de a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$) et a accélération gravitationnelle ($g$) en utilisant :
| $ F = S h \rho_w g $ |
Étant donné que a masse de colonne de liquide ($M$) dépend de a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) selon l'équation :
| $ M = \rho_w S h $ |
et que a force de la colonne ($F$) est représenté par a accélération gravitationnelle ($g$) par :
| $ F_g = m_g g $ |
alors l'expression peut être écrite comme suit :
| $ F = S h \rho_w g $ |
.
ID:(4248, 0)
Définition de la pression
Équation
A pression de la colonne d'eau ($p$) se calcule à partir de a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) comme suit :
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Pression de colonne
Équation
Si l'on considère l'expression de a force de la colonne ($F$) et qu'on la divise par a hauteur de la colonne de liquide ($S$), on obtient a pression de la colonne d'eau ($p$). Au cours de ce processus, nous simplifions a hauteur de la colonne de liquide ($S$), de sorte qu'il ne dépende plus de lui. L'expression résultante est la suivante :
| $ p = \rho_w g h $ |
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
ID:(4249, 0)
Pression de colonne avec pression atmosphérique
Équation
A pression de la colonne d'eau ($p$) est avec a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$), a accélération gravitationnelle ($g$) et a pression atmosphèrique ($p_0$) égal à :
| $ p_t = p_0 + \rho_w g h $ |
ID:(4250, 0)
Différence de hauteur
Équation
Lorsque deux colonnes de liquide sont connectées avec a hauteur de colonne de liquide 1 ($h_1$) et a hauteur de colonne de liquide 2 ($h_2$), une a différence de hauteur ($\Delta h$) est formée, qui est calculée comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de hauteur ($\Delta h$) générera la différence de pression qui fera s'écouler le liquide de la colonne la plus élevée vers la colonne la plus basse.
ID:(4251, 0)
Différence de pression
Équation
Lorsque deux colonnes de liquide sont connectées avec a pression dans la colonne 1 ($p_1$) et a pression dans la colonne 2 ($p_2$), une a différence de pression ($\Delta p$) est créée, qui est calculée selon la formule suivante :
| $ \Delta p = p_2 - p_1 $ |
a différence de pression ($\Delta p$) représente la différence de pression qui fera s'écouler le liquide de la colonne la plus haute vers la colonne la plus basse.
ID:(4252, 0)
Différence de pression entre les colonnes
Équation
La différence de hauteur, représentée par a différence de hauteur ($\Delta h$), implique que la pression dans les deux colonnes est différente. En particulier, a différence de pression ($\Delta p$) est une fonction de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), et a différence de hauteur ($\Delta h$), comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
S'il existe a différence de pression ($\Delta p$) entre deux points, comme le détermine l'équation :
| $ \Delta p = p_2 - p_1 $ |
nous pouvons utiliser a pression de la colonne d'eau ($p$), qui est définie comme suit :
| $ p_t = p_0 + \rho_w g h $ |
Cela donne :
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Comme a différence de hauteur ($\Delta h$) est définie comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de pression ($\Delta p$) peut être exprimée comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)